Mat_Analiz_Prokhorov

f (x)dx

a

условно сходится, если он сходится, а несобственный интеграл Римана

f (x) dx

a

расходится. В дальнейшем мы приведем пример, показывающий существование условно сходящихся несобственных интегралов Римана.

3. Признак Дирихле сходимости несобственных интегралов Римана

Признаки мажорации и сравнения могут проверить лишь абсолютную сходимость несобственных интегралов. В настоящей части установим признаки сходимости, способные тестировать и условно сходящиеся несобственные интегралы. Начнем с признака, известного как признак Дирихле.

Теорема 2 Пусть функции f и g удовлетворяют следующим условиям: (а) функция f монотонна на полуоси [a, ) и limx f(x) = 0;

(б) для любого b > a функция g интегрируема по Риману на отрезке [a, b] и функция G,

G(b) b g (x)dx,

a

ограничена на полуоси (a, ).

Тогда несобственный интеграл Римана

( fg )(x)dx

a

сходится.

Доказательство. Монотонная функция f интегрируема по Риману на отрезке [a, b] и поэтому произведение fg интегрируемых функций также интегрируемо по Риману на этом отрезке.

Ограниченность функции G означает, что для всех b > a выполняется неравенство G(b) M с некоторым M 0.

291

По определению limx f(x) = 0, если

> 0 b x x > b f(x) < .

Пусть b > b и b > b . По второй теореме о среднем значении найдется точка [b , b ] такая, что

f (b') G( ) G(b') f (b") G(b") G( )

f (b') G( ) G(b') f (b") G(b") G( )

M M M M 4M ,

что выражает критерий Коши сходимости несобственного интеграла Римана от произведения fg на полуоси [a, ). Следовательно, этот несобственный интеграл Римана сходится, что заканчивает доказательство теоремы 2.

Пример. Рассмотрим несобственный интеграл Римана

sin x dx

1 x

и покажем, что он условно сходится. Его сходимость проверяется признаком Дирихле, потому что функция f, f(x) = 1/x,

монотонно стремится к нулю при x , а функция g, g(x) = sin x, обладает тем свойством, что интеграл с переменным верхним пределом

292

bb

G(b) g (x)dx sin xdx cosb cos1

11

ограничен, G(b) cos b + cos 1 < 2. Аналогичным образом устанавливается, что несобственный интеграл Римана

cos2x dx

1 x

сходится. Следовательно, интеграл с переменным верхним пределом интегрирования

является непрерывной функцией на любом отрезке [a, b] и имеет предел при b . Поэтому функция H ограничена на полуоси [1, ), H(b) C, b 1.

Теперь покажем, что наш несобственный интеграл не сходится абсолютно. Действительно,

является неограниченной функцией переменного b и поэтому несобственный интеграл Римана

расходится.

293

4. Признак Абеля сходимости несобственных интегралов Римана

Следующая теорема известна как признак Абеля сходимости несобственного интеграла Римана.

Теорема 3 Пусть функции f и g удовлетворяют следующим условиям:

(а) функция f монотонна и ограничена на полуоси [a, );

(б) для любого b > a функция g интегрируема по Риману на отрезке [a, b] и несобственный интеграл Римана

g(x)dx

a

сходится.

Тогда несобственный интеграл Римана

( fg )(x)dx

a

сходится.

Доказательство. Монотонная функция f интегрируема по Риману на отрезке [a, b] и поэтому произведение fg интегрируемых функций также интегрируемо по Риману на этом отрезке.

Ограниченность функции f означает, что для всех x a выполняется неравенство f(x) M с некоторым M 0. По критерию Коши несобственного интеграла Римана от функции g на полуоси [a, )

> 0 b',b"b' > b и b"> b' b" g(x)dx .

b'

Пусть b > b и b > b . По второй теореме о среднем значении найдется точка [b , b ] такая, что

294

что выражает критерий Коши сходимости несобственного интеграла Римана от произведения fg на полуоси [a, ). Следовательно, этот несобственный интеграл Римана сходится, что заканчивает доказательство теоремы 3.

Условия признаков Дирихле и Абеля весьма схожи, но первое условие признака Абеля ослабляет требование первого условия признака Дирихле, тогда как второе условие признака Абеля усиливает соответствующее условие признака Дирихле.

295

Лекция 30.

1. Простейшая задача интерполирования

2. Погрешность приближения функции интерполяционным многочленом первой степени

3. Погрешность приближения функции интерполяционным многочленом второй степени

1. Простейшая задача интерполирования

В математическом анализе возникает потребность восстановления функции f по ее значениям в точках x0, x1, ..., xn. Конечно, есть немало способов построения таких функций. Задача имеет много решений, из которых желательно выбрать простейшее, например, отыскать многочлен. Обычно простейшая задача интерполирования понимается так: ищется многочлен

Lm(x) = a0xm + a1xm 1 + ... + am 1x + am

наименьшей степени m, который в заданных точках x0 < x1 < ... < xn принимает заданные значения y0, y1, ..., yn.

Если yk = f(xk), k = 0, 1, ..., n, то найденный интерполяционный многочлен Lm приближает функцию f на заданном отрезке [a, b]. Имея интерполяционную формулу

f(x) = Lm(x) + Rm(x),

следует оценить погрешность приближения Rm(x).

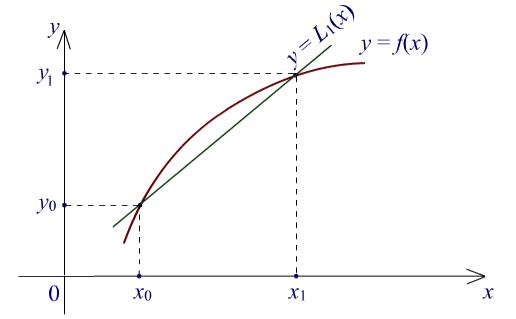
Мы не будем решать простейшую интерполяционную задачу в общем виде, а приведем только интерполяционные многочлены Лагранжа в частных случаях n = 0, 1, 2.

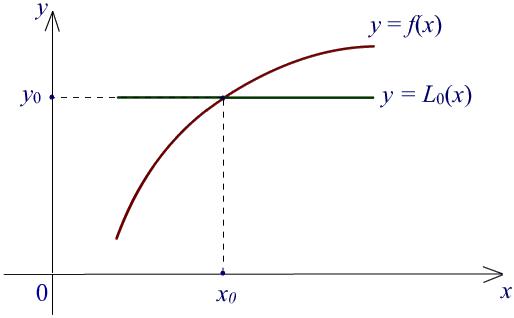
Интерполяционный многочлен нулевой степени. Если n = 0, то интерполяционный многочлен Лагранжа L0 нулевой степени,

L0(x) = y0,

решает интерполяционную задачу, так как L0(x0) = y0 и степень многочлена минимальна.

296

Рис. 1. Иллюстрация приближения функции f(x) многочленом нулевой степени

Интерполяционный многочлен первой степени. Если n = 1 то интерполяционный многочлен Лагранжа L1 степени не выше первой,

решает интерполяционную задачу. Действительно, подставляя в формулу для L1(x) значения x0 и x1, непосредственно

убеждаемся, что L1(x0) = y0 и L1(x1) = y1. Если y0 y1, то есть точки (x0, y0) и (x1, y1) не лежат на одной горизонтальной прямой, то степень интерполяционного многочлена понизить нельзя.

Рис. 2. Иллюстрация приближения функции f(x) многочленом первой степени

Интерполяционный многочлен второй степени. Если n = 2, то интерполяционный многочлен Лагранжа L2 степени не выше второй,

297

решает интерполяционную задачу. Действительно, подставляя в формулу для L2(x) значения x0, x1 и x2, непосредственно

убеждаемся, что L2(x0) = y0, L2(x1) = y1 и L2(x2) = y2. Если точки (x0, y0), (x1, y1) и (x2, y2) не лежат на одной прямой, то степень интерполяционного многочлена понизить нельзя.

298

Рис. 3. Иллюстрация приближения функции f(x) многочленом третьей степени

2. Погрешность приближения функции интерполяционным многочленом первой степени

Оценим погрешность R1(x) = f(x) L1(x) приближения функции f ее интерполяционным многочленом Лагранжа L1.

Теорема 1 Пусть функция f дважды дифференцируема на отрезке [x0, x1] и на этом отрезке выполняется неравенство f

(x) M. Тогда для погрешности R1(x) = f(x) L1(x) приближения функции f ее интерполяционным многочленом Лагранжа L1 на отрезке [x0, x1] справедлива оценка

Доказательство. Выберем произвольно число K и обозначим

откуда следует, что (x0) = 0 и (x1) = 0 и

299

R1(x) = (x) + K(x x0)(x x1).

Функция , как и функция f, дважды дифференцируема на отрезке [x0, x1]. Зафиксируем произвольно x (x0, x1) и потребуем, чтобы выполнилось условие (x ) = 0, которое равносильно равенству

При таком выборе числа K функция обращается в нуль в точках x0, x и x1.

Рис. 4. Иллюстрация к доказательству теоремы о погрешности приближения функции интерполяционным многочленом первой степени

По теореме Ролля найдутся точки 1 (x0, x ) и 2 (x , x1) такие, что( 1) = 0 и ( 2) = 0.

На этот раз применим теорему Ролля к функции на отрезке [ 1, 2], согласно которой найдется точка ( 1, 2) такая, что

( ) = 0.

Но L 1(x) тождественно обращается в нуль на всей числовой оси, потому что L1 является линейной функцией. Краткими вычислениями находим, что [(x x0)(x x1)] = 2. Следовательно, условие ( ) = 0 равносильно уравнению

300