
Mat_Analiz_Prokhorov
.pdf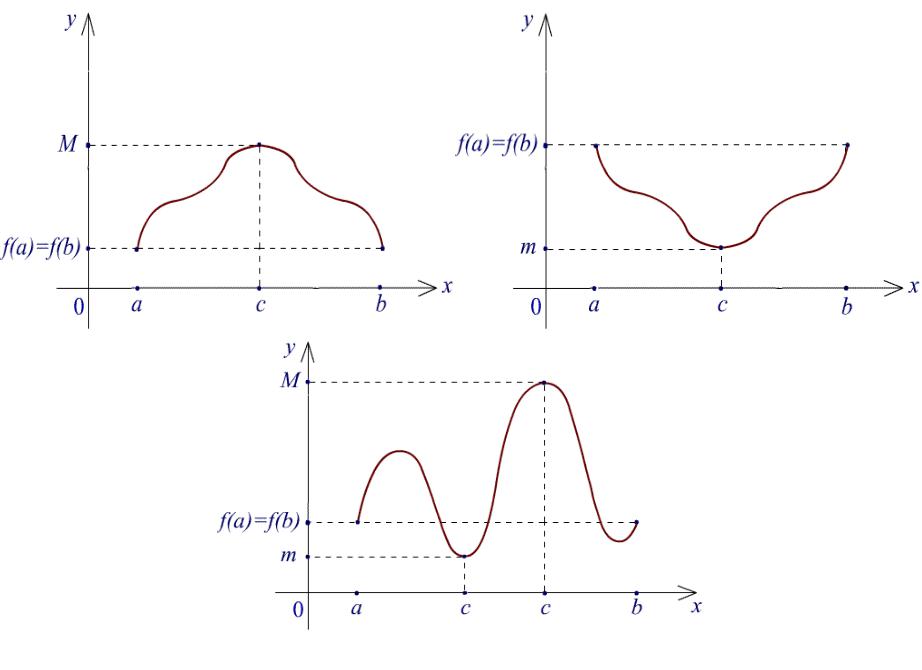
161

Рис. 1. Возможные сценарии поведения функции f.
Обозначим через c ту из точек x1 или x2, которая окажется внутри (a, b). Поскольку функция f дифференцируема в точке c и имеет в ней экстремум, то по теореме Ферма f (c) = 0, что доказывает теорему 1.
2. Теорема Лагранжа о среднем значении
Обобщением теоремы Ролля служит следующая теорема Лагранжа.
Теорема 2. Пусть функция f удовлетворяет условиям:
1.непрерывна на отрезке [a, b];
2.дифференцируема на интервале (a, b).
Тогда существует точка c (a, b) такая, что справедлива формула
f '(c) f (b) f (a) . b a
Доказательство. Составим функцию
g(x) f (x) x, |
|
f (b) f (a) |
. |
|
|||
|
|
b a |
|
Функция g как сумма функции f и линейной функции обладает свойствами:
1.непрерывна на отрезке [a, b];
2.дифференцируема на интервале (a, b);
3.g(a) = g(b), что легко проверяется прямой подстановкой
162

g(a) f (a) f (b) f (a) a b a
g(b) f (b) f (b) f (a) b b a
f (a)b f (a)a f (b)a f (a)a |
|
f (a)b f (b)a |
, |
||
b a |
|
|
|
b a |
|
f (b)b f (b)a f (b)b f (a)b |
|
f (b)a f (a)b . |
|||
b a |
|
|
|
b a |
|
Таким образом, функция g удовлетворяет условиям теоремы Ролля, согласно которой существует точка c (a, b) такая, что g (c) = 0, то есть
f '(c) f (b) f (a) 0, b a
что доказывает теорему 2.
Теорема 2 имеет интересное геометрическое истолкование. Отношение
f (b) f (a)
b a
выражает тангенс угла, образованного хордой, соединяющей крайние точки a = (a, f(a)) и b = (b, f(b)) графика функции f, и
осью OX, в то время как f (c) равно тангенсу угла наклона касательной к графику функции f в точке x0 к положительному направлению оси OX. В теореме 2 утверждается существование точки c, в которой касательная к графику функции параллельна хорде, соединяющей крайние точки A и B графика.
163
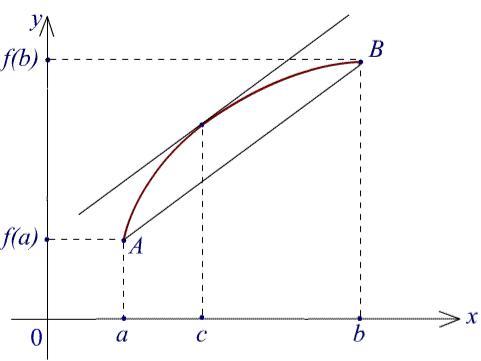
Рис. 2. Геометрическая иллюстрация теоремы Лагранжа.
3. Теорема Коши о среднем значении
Дальнейшее обобщение теорем Ролля и Лагранжа дает следующая теорема Коши.
Теорема 3. Пусть функции f и g удовлетворяют условиям:
1.непрерывны на отрезке [a, b];
2.дифференцируемы на интервале (a, b);
3.g(a) g(b) и g (x) 0 для всех x (a, b).
Тогда существует точка c (a, b) такая, что справедлива формула
164

f '(c) f (b) f (a) . g' (c) g (b) g (a)
Доказательство. Составим функцию
h(x) f (x) g(x), |
|
f (b) f (a) |
. |
|
|||
|
|
g(b) g(a) |
|
Функция h как линейная комбинация функций f и g обладает свойствами:
1.непрерывна на отрезке [a, b];
2.дифференцируема на интервале (a, b);
3.h(a) = h(b), что легко проверяется прямой подстановкой
h(a) f (a)
h(b) f (b)
f (b) f (a) g(b) g(a)
f (b) f (a) g (b) g(a)
g(a) f (a)g (b) f (a)g(a) f (b)g(a) f (a)g(a) g(b) g(a)
f (a)g(b) f (b)g(a) , g(b) g(a)
g(b) f (b)g (b) f (b)g(a) f (b)g(b) f (a)g(b) g (b) g (a)
f (b)g(a) f (a)g (b) g(b) g (a)
165

Таким образом, функция h удовлетворяет условиям теоремы Ролля, согласно которой существует точка c (a, b) такая, что h (c) = 0, то есть
f '(c) f (b) f (a) g' (c) 0, g(b) g(a)
что доказывает теорему 3.
4. Правило Лопиталя для отношения бесконечно малых
Следующие теоремы, известные под названием правила Лопиталя для отношения бесконечно малых или бесконечно больших функций, предлагают эффективный метод отыскания предела функции при помощи средств дифференциального исчисления. Метод не является всеобщим или универсальным, но приводит к быстрому достижению цели во многих задачах. Начнем с задачи о пределе отношения бесконечно малых.
Теорема 4. Пусть функции f и g удовлетворяют условиям:
1.дифференцируемы в некоторой -окрестности точки x0, за исключением, быть может, самой точки x0;
2.limx x0f(x) = limx x0g(x) = 0;
3.g (x) 0, если 0 < x x0 < , и существует предел
lim f '(x) l, x x0 g '(x)
Тогда существует предел
lim f (x) ,
x x0 g(x)
который равен l.
166

Доказательство. Доопределим функции f и g в точке x0, положив f(x0) = g(x0) = 0. При таком доопределении окажется, что
limx x0 f(x) = f(x0) = 0 и |
limx x0 g(x) = g(x0) = 0. |
Следовательно, обе доопределенные функции f и g стали непрерывными в точке x0.
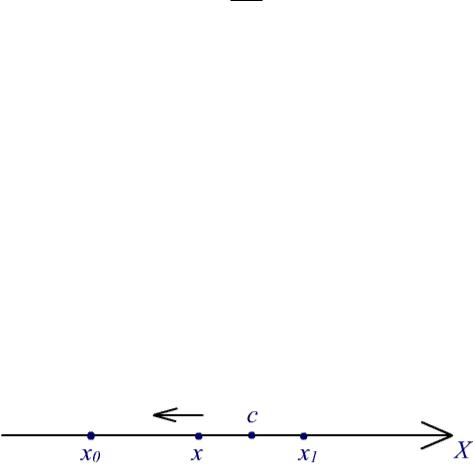
Пусть x > x0, x x0 < . функции f и g непрерывны на отрезке [x0, x] и дифференцируемы в его внутренних точках. Применяя к функции g теорему Лагранжа, найдем точку c (x0, x) такую, что
g(x) = g(x) g(x0) = g (c)(x x0).
Рис. 3. Иллюстрация к теореме о правиле Лопиталя для отношения бесконечно малых.
Поскольку g (c) 0, то и g(x) 0.
Теперь согласно теореме Коши, примененной к f и g, найдется точка c (x0,x) такая, что
f '(c) |
|
f (x) f (x0 ) |
|
f (x) |
|
g' (c) |
g(x) g(x ) |
g(x) |
|||
|
|
||||
|
|
0 |
|
|
Если x x0, то тем более c x0, поэтому существует правосторонний предел левой части последнего равенства, а следовательно, и правой части и справедлива формула
lim |
f (x) |
|
lim |
f '(c) |
|
lim |
f '(c) |
l. |
|
g(x) |
g '(c) |
g '(c) |
|||||||
x x0 0 |
|
x x0 0 |
|
c x0 0 |
|
Симметричными рассуждениями покажем, что
167
lim |
f (x) |
l. |
|
g(x) |
|||
x x0 0 |
|
Из двух последних равенств следует, что
lim |
f (x) |
l. |
|
g (x) |
|||
x x0 |
|
что заканчивает доказательство теоремы 4.
Несмотря на привлекательность и простоту правила Лопиталя, хотелось бы предостеречь от желания применить его в двух фундаментальных примерах
lim sin x |
1 и |
lim log(1 x) |
1. |
||
x x0 |
x |
|
x 0 |
x |
|
Оба предела по существу определяют значения производных функций y = sin x и y = log(1 + x) в точке 0. Это глубокие результаты, они могут быть получены при помощи тонких рассуждений. Попытка упростить трудный подход, подменив его правилом Лопиталя, приведет к логическому порочному кругу: знание производных основано на знании пределов, а знание пределов основано на правиле Лопиталя, использующем значения производных.
5. Правило Лопиталя для отношения бесконечно больших
Выведем аналогичное правило Лопиталя для отношения бесконечно больших.
Теорема 5. Пусть функции f и g удовлетворяют условиям:
1.дифференцируемы в некоторой -окрестности точки x0, за исключением самой точки x0;
2.limx x0f(x) = limx x0g(x) = ;
3.g (x) 0, если 0 < x x0 < , и существует предел
168
lim |
f '(x) |
l. |
|
g '(x) |
|||
x x0 |
|
Тогда существует предел
lim f (x) ,
x x0 g(x)
который равен l.
Доказательство. Так как limx x0f(x) = limx x0g(x) = , то f(x) 0 и g(x) 0, если x находится достаточно близко к x0. Будем считать эти условия выполненными за счет выбора достаточно малого > 0.
Запишем по определению предела функции
(1) |
> 0 1 |
|
> 0 x x0 |
|
x x0 |
|
|
|
1 |
|
f '(x) |
l |
, |
|||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
|
|
g' (x) |
||||||||||||||||||||||||||||||
откуда, в частности, следует неравенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|
|
f ' (x) |
|
|
|
f ' (x) |
l l |
|
|
|
|
|
|
f '(x) |
l |
|
|
|
l |
|
|
|
|
l |
|
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
g '(x) |
g'(x) |
|
|
|
|
g'(x) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пусть x1 > x0, x1 x0 < 1. Выберем точку x (x0, x1).
Рис. 4. Иллюстрация к теореме о правиле Лопиталя для отношения бесконечно больших.
169

Функции f и g дифференцируемы на отрезке [x, x1]. Так как limx x0f(x) = limx x0g(x) = , то f(x) f(x1) и g(x) g(x1) при фиксированном x1 и при x, находящихся достаточно близко к x0. Будем считать эти условия также выполненными за счет
выбора достаточно малого 1 > 0.
Теперь согласно теореме Коши, примененной к функциям f и g на отрезке [x, x1], найдется точка c (x, x1) такая, что
f '(c) f (x1 ) f (x) . g' (c) g (x1 ) g (x)
Преобразуем эту формулу к виду
|
|
f (x) |
f (x1 ) |
1 |
||
f '(c) |
f (x) |
|||||
|
|
|
. |
|||
g' (c) |
g (x) |
g(x1 ) |
|
|||
|
|
|
1 |
|||
|
g(x) |
|||||
|
|
|
|
|
||
Разрешим это равенство относительно f(x)/g(x)
|
|
f ' (c) |
g(x1 ) |
1 |
||
f (x) |
|
g (x) |
||||
|
|
|
|
. |
||
g(x) |
g'(c) |
|
f (x1 ) |
|
||
|
|
|
|
1 |
||
|
|
|
f (x) |
|||
|
|
|
|
|
|
|
Вычтем l из обеих частей равенства и проведем тождественные преобразования
f (x) l g(x)
f ' (c)
g'(c)
g (x1 ) |
|
1 |
|
|
|
|||
|
g (x) |
|
|
f '(c) |
l. |
|||
|
|
|
|
|
|
1 |
|
|
|
f (x1 ) |
|
|
g'(c) |
||||
|
1 |
|
|
|||||
|
|
|||||||
|
f (x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Отсюда получим оценки модуля
170
