Mat_Analiz_Prokhorov

Поскольку неравенство x x0 < равносильно объединению неравенств x0 < x x0 и x x0 + , то последнее условие означает, что

что доказывает необходимость условия теоремы 2.

Перейдем к доказательству достаточности условия теоремы 2. Пусть функция f имеет в точке x0 предел слева и предел справа, которые равны числу l. Тогда по определению Коши

> 0 1 > 0 x X x0 1 < x < x0 f(x) l <

и

> 0 2 > 0 x X x0 < x < x0 + 2 f(x) l < .

Обозначим = min{ 1, 2}. Тогда условие x x0 < влечет неравенства x0 1 < x x0 или x0 x < x0 + 2. Объединяя два последних условия, запишем совокупное условие

> 0 > 0 x X, x x0, x x0 < f(x) l < ,

которое означает, что l = limx x0f(x) и доказывает достаточность условия теоремы 2.

Теорема 2 доказана полностью.

Если в теореме 2 включить в рассмотрение точку x0 и положить f(x0) = l, то приходим к утверждению: функция f непрерывна в точке x0 тогда и только тогда, когда f непрерывна слева и непрерывна справа в этой точке.

121

3. Односторонние пределы монотонной функции

Напомним характеристики монотонной функции.

Определение 4. Пусть функция f определена на отрезке [a, b]. Функция f называется · неубывающей, если x1, x2 [a, b] x1 < x2

f(x1) f(x2); · возрастающей, если x1, x2 [a, b] x1 < x2 f(x1) < f(x2); · невозрастающей, если x1, x2 [a, b] x1 < x2 f(x1) f(x2); · убывающей, если x1, x2 [a, b] x1 < x2 f(x1) > f(x2); · монотонной, если она не убывает или не возрастает; · строго монотонной, если она возрастает или убывает.

Аналогичные определения возможны для интервала (a, b) или для множеств [a, b) и (a, b].

Покажем, что монотонные функции имеют односторонние пределы в каждой точке.

Теорема 3. Пусть функция f монотонна в некоторой -окрестности точки x0. Тогда f имеет односторонние пределы в точке x0.

122

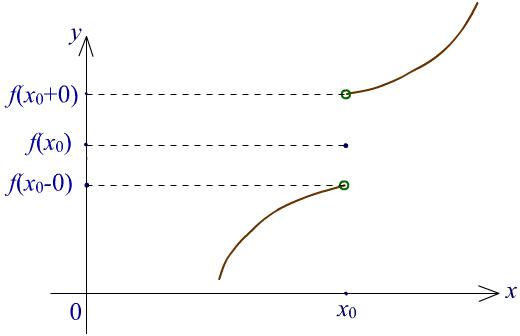
Рис. 3. Иллюстрация к теореме о существовании односторонних пределов.

Доказательство. Теорема 3 содержит четыре симметричных утверждения о существовании предела слева и предела справа для неубывающих и невозрастающих функций. Проведем подробное доказательство лишь для одного из случаев, подразумевая, что остальные ему аналогичны.

Пусть функция f не убывает. Покажем, что она имеет предел слева в точке x0. Поскольку f(x) f(x0) для всех x (x0 , x0), то множество значений {f(x): x0 < x < x0} ограничено сверху и поэтому имеет верхнюю грань. Обозначим

и докажем, что

123

По свойству верхней грани

> 0 x (x0 , x0) f(x ) > .

Обозначим 1 = x0 x > 0. Благодаря монотонности функции и свойству верхней грани f(x ) f(x) для всех x (x , x0).

Так как система неравенств < f(x) влечет неравенство f(x) < , то последнее условие определяет как предел слева функции f в точке x0 и доказывает теорему 3.

124

В процессе доказательства, помимо качественного заключения теоремы 3, мы установили, что для неубывающей функции f

4. Классификация точек разрыва функции

Разумеется, непрерывные функции проще в исследовании, чем разрывные. Однако следует уметь работать и с разрывными функциями, для чего важно знать, как ведет себя функция в окрестности точки разрыва. Дадим классификацию точек разрыва.

Определение 5. Пусть функция f определена в -окрестности точки x0. Точка x0 называется точкой устранимого разрыва функции f, если f имеет предел в точке x0, но

125

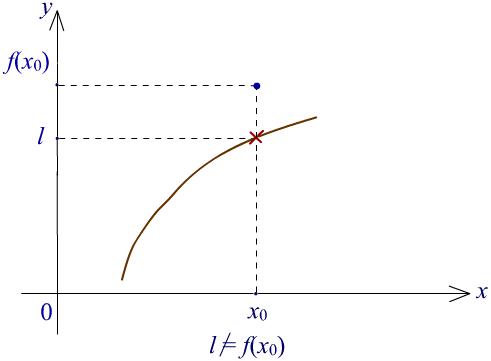
Рис. 5. Иллюстрация к определению точки устранимого разрыва.

Терминология вполне объяснима. Действительно, достаточно подправить функцию, изменив ее только в одной точке x0 и положив f x0 limx x0 f x , как исправленная функция станет непрерывной в точке x0.

Определение 6. Пусть функция f определена в -окрестности точки x0. Точка x0 называется точкой разрыва 1 рода функции f, если f имеет предел слева и предел справа в точке x0, но

126

См рис. 3.

Определение 7. Точка разрыва функции f называется точкой разрыва 2 рода, если она не является точкой устранимого разрыва или точкой разрыва 1 рода.

Рис. 6. Иллюстрация к определению точек разрыва первого и второго рода.

5. Символы O и o

Распространим определение предела функции на случай бесконечно удаленной точки. Начнем с определения Коши. Определение 8. Пусть функция f определена для всех x a. Число l называется пределом функции f при x , если

> 0 M > a x > M f(x) l < ,

127

и обозначается limx f(x).

Предел limx f(x) определяется симметрично.

Полезно также описание функций, стремящихся к бесконечности.

Определение 9. Говорят, что функция f стремится к при x x0 на множестве X, если

M > 0 x X, x x0, x x0 < f(x) > M.

Описание функций, стремящихся к , дается симметрично.

Введем терминологию, частично заимствованную из теории последовательностей. Определение 10. Функция f называется бесконечно малой при x x0, если

lim f x 0.

x x0

Определение 11. Функция f называется бесконечно большой при x x0, если f(x) стремится к при x x0. Теперь введем O- и o-символику для сравнения бесконечно малых и бесконечно больших функций. Определение 12. Пусть функции f и g бесконечно малы при x x0 и

Если l = 1, то функции f и g называются эквивалентными.

128

Если l = 0, то говорят, что бесконечно малая функция f более высокого порядка, чем бесконечно малая функция g, и пишут f(x) = o(g(x)) при x x0.

Если дробь (f(x)/g(x)) ограничена в -окрестности точки x0, то пишут f(x) = O(g(x)) при x x0.

Например, x2 = o(x) при x 0, а xsin x = O(x) при x 0.

Определение 13. Пусть функции f и g являются бесконечно большими при x x0 и

Если l = 1, то функции f и g называются эквивалентными.

Если l = 0, то говорят, что бесконечно большая функция f более низкого порядка, чем бесконечно большая функция g, и пишут f(x) = o(g(x)) при x x0.

Если дробь f(x)/g(x) ограничена в -окрестности точки x0, то пишут f(x) = O(g(x)) при x x0.

Определения 10-13 имеют смысл и для x0 = или x0 = .

129

Лекция 13

1. Равномерная непрерывность

2. Теорема Кантора

3. Первая теорема Вейерштрасса

4. Вторая теорема Вейерштрасса

5. Лемма о вложенных отрезках

1. Равномерная непрерывность

От понятия непрерывности в точке перейдем к понятию непрерывности на множестве.

Определение 1. Функция f называется непрерывной на множестве X, если она непрерывна в каждой точке этого множества.

Используя определение непрерывности в точке, дадим логическое определение непрерывности на множестве. Именно, функция f, определенная на множестве X, непрерывна на этом множестве, если

x0 X > 0 > 0 x X x x0 < f(x) f(x0) < .

В этом определении число зависит от и от x0. Более сильное требование заключается в наличии универсального для всех x0, зависяшего только от .

Определение 2. Функция f называется равномерно непрерывной на множестве X, если

> 0 > 0 x, x X x x < f(x) f(x ) < .

Очевидно, что равномерная непрерывность на множестве X влечет непрерывность на этом множестве. Покажем на примерах, что обратное неверно.

Пример 1. Пусть f(x) = x2, X = . Предположим, что f равномерно непрерывна на X. Тогда

> 0 > 0 x, x X x x < x2 x 2 < .

Положим, например, в последнем неравенстве x x = /2 и получим

130