Mat_Analiz_Prokhorov

Он заключается в проверке справедливости некоторого свойства A = A(n) для всех натуральных чисел n. Применение полной математической индукции состоит в проверке справедливости свойства A(1) для единицы, высказывании гипотезы о справедливости свойства A(n) и проверке свойства A(n + 1) для числа n + 1.

2. Сумма всех членов бесконечно убывающей геометрической прогрессии.

Геометрическая прогрессия задается начальным элементом b и знаменателем q. Геометрическая прогрессия называется бесконечно убывающей, если q < 1. Не вдаваясь на настоящем этапе в строгий смысл понятия суммы

b + bq + bq2 + ... + bqn 1 + ...

всех членов прогрессии, будем принимать, что она равна b/(1 q).

3. Концепция действительного числа.Воспримем конструкцию, согласно которой всякое действительное a число изображается бесконечной десятичной дробью. Точнее,

a = a0 + 0. 1 2... n... ,

где a0 - целое число, называемое целой частью действительного числа a, а 1, 2,..., n,... - цифры 0, 1 , ..., 9. Рациональные числа изображаются периодическими дробями, иррациональным числам соответствуют непериодические разложения. В отдельных случаях возникает двойственное представление одного и того же действительного числа разными бесконечными десятичными дробями. Это происходит с числами, имеющими 0 или 9 в периоде. Именно, числа

и

a0 + 0. 1... n 1( n + 1)00...0...

равны между собой, поскольку

11

Если двойственное представление нежелательно, то условимся, например, что бесконечная десятичная дробь не имеет 9 в периоде.

Над действительными числами можно производить арифметические операции, хотя в средней школе не задаются вопросом о техническом исполнении действий над бесконечными десятичными дробями. Проиллюстрируем очевидный подход на примере сложения двух чисел

a = a0 + 0. 1 2... n...

и

b = b0 + 0. 1 2... n... .

Складываем постепенно

a0 + b0,

(a0 + 0. 1) + (b0 + 0. 1),

12

(a0 + 0. 1 2) + (b0 + 0. 1 2)

и так далее. Обозначим

(a0 + 0. 1 2... n) + (b0 + 0. 1 2... n) = c0n + 0. 1n 2n... nn.

Целые числа c01, c02, ..., c0n, ... образуют неубывающую последовательность. Начиная с некоторого номера n0, все числа c0n,c0n+1,...

будут оставаться одинаковыми. Это число примем за c0. Аналогично для всякого k цифры kk, kk+1, ..., kn, ... образуют неубывающую последовательность. Начиная с некоторого номера nk, все цифры kn, kn+1, ... будут оставаться одинаковыми. Эту цифру примем за k. Таким образом, появляется бесконечная десятичная дробь

c = c0 + 0. 1 2... n...,

равная сумме a + b.

Обозначим через множество всех действительных чисел. Арифметические операции над действительными числами подчиняются следующим условиям:

1.(a + b) + c = a + (b + c) - ассоциативность сложения;

2.a + b = b + a - коммутативность сложения;

3.для любого a справедливо равенство a + 0 = a - роль 0 в сложении;

5.(ab)c = a(bc) - ассоциативность умножения;

6.ab = ba - коммутативность умножения;

13

7.для любого a справедливо равенство 1a = a - роль единицы в умножении;

8.для любого a , a 0, существует число a 1 такое, что aa 1 = 1 - возможность деления;

9.a(b + c) = ab + ac - дистрибутивность.

Пусть даны два действительных числа

a = a0 + 0. 1 2... n...

и

b = b0 + 0. 1 2... n...,

десятичные записи которых не содержат 9 в периоде. Неравенство a < b справедливо в том случае, если либо a0 < b0, либо

существует номер n такой, что a0 = b0, 1 = 1, ..., n 1 = n 1, но n < n. Продолжим перечень свойств действительных чисел, относящихся к неравенствам:

10.если a < b и b < c, то a < c - транзитивность неравенств;

11.если a < b, то для любого c справедливо неравенство a + c < b + c;

12.если a < b, то для любого c > 0 справедливо неравенство ac < bc. Кроме того, очевидно свойство

13.для любого a существует целое число k такое, что a < k - аксиома Архимеда.

14

Отметим, что свойствам 1-13 удовлетворяет не только множество действительных чисел, но и множество рациональных чисел. В дальнейшем мы обнаружим еще одно свойство, которое присуще множеству , но не выполняется в множестве рациональных чисел.

4. Множества и действия над ними

Напомним известные операции над множествами.

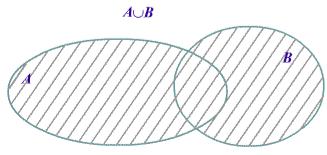
Определение 1. Множество C называется объединением множеств A и B, C = A B, если C состоит из всех элементов, каждый из которых принадлежит A либо B.

Рис. 1. Объединение множеств.

Определение 2. Множество C называется пересечением множеств A и B, C = A B, если C состоит из всех элементов, каждый из которых одновременно принадлежит A и B.

15

Рис. 2. Пересечение множеств.

Определение 3. Множество C называется разностью множеств A и B, C = A\B, если C состоит из всех элементов, каждый из которых принадлежит A, но не принадлежит B.

Рис. 3. Разность множеств.

В частности, если B A, то A\B называется дополнением B в A.

16

Рис. 4. Дополнение B в A.

Можно использовать и другие операции над множествами, однако нам в дальнейшем потребуются лишь определения 1-3.

Есть немало формул, связывающих различные операции между собой. Покажем, например, что если B A, то A = B (A\B), причем B (A\B) = , где - пустое множество.

Действительно, если x B, то x A\B и следовательно, B и A\B имеют пустое пересечение. Кроме того, если x A,то возможно одно из двух: либо x B, либо x A\B. Таким образом,

A(B (A\B)).

Сдругой стороны, если x B, то x A и если x A\B, то x A. Таким образом, (B (A\B)) A,

что вместе с предыдущим включением доказывает нужную формулу о совпадении A и B (A\B).

5. Отображения множеств

Определим некоторые множества по их характеристикам.

17

Определение 4. Отображение f: X Y называется отображением множества X на множество Y, если для всякого элемента yY найдется элемент x X такой, что f(x) = y.

Обращаем внимание, что предлог "на" в определении 4 является частью названия. Другими словами, определение 4 ввело термин "отображение на".

Определение 5. Отображение f: X Y называется взаимно однозначным, если оно отображает X на Y и для всякого элемента yY существует единственный элемент x X такой, что f(x) = y.

Очевидно, что только взаимно однозначное отображение допускает обратное отображение.

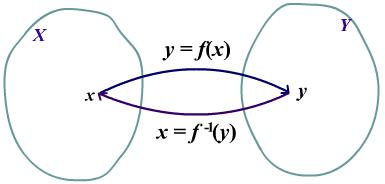
Определение 6. Пусть f: X Y - взаимно однозначное отображение. Тогда отображение g: Y X называется обратным к f, если g всякому элементу y Y сопоставляет такой элемент x X, для которого f(x) = y. Обозначим g = f 1.

Таким образом,

y = f(x) x = f 1(y).

Рис. 5. Взаимно однозначное отображение.

18

Определение 7. Пусть f: X Y и g: Y Z. Тогда отображение h: X Z называется сложным отображением, или композицией отображений f и g, h = g f, если h отображает всякий элемент x X на элемент z Z такой, что z = g(y), где y = f(x).

Операционно сложное отображение можно записать формулой z = g(f(x)).

Рис. 6. Сложное отображение.

19

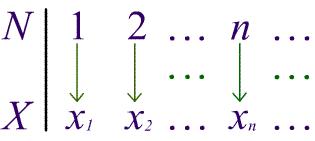
Лекция 2.

1.Счетные множества и их свойства

2. Бесконечные подмножества счетного множества

3. Счетное объединение счетных множеств

4. Несчетность множества действительных чисел

1.Счетные множества и их свойства

Бесконечные множества разумно сравнивать друг с другом при помощи взаимно однозначных отображений.

Определение 1. Множества X и Y называются равномощными, если существует взаимно однозначное отображение одного множества на другое. В качестве тестового множества для сравнения естественно брать самое простое, ясно устроенное множество, каким является, в частности, множество натуральных чисел 1, 2, ..., n, ....

Определение 2. Множество X называется счетным, если оно равномощно множеству .

Взаимно однозначное отображение множества на счетное множество X логично установить, присвоив каждому элементу x X номер в виде натурального числа.

Рис. 1. Взаимно однозначное отображение

20