Mat_Analiz_Prokhorov

Из неравенства

p yn yn p <

следует, что

yn > p .

Напомним, что p 0. Выберем

= 2p > 0

и находим, что для n > n0 справедливо неравенство

yn > p p2 = 2p ,

а следовательно,

1 < 2 .

yn p

Последнее неравенство выражает свойство ограниченности множества

а значит, и ограниченности множества

51

которое объединяет одно конечное (то есть ограниченное) и другое ограниченное множества. Окончательно получили, что обе последовательности (7) бесконечно малы, потому что каждая из них представляет собой произведение бесконечно малой и ограниченной последовательностей. По лемме 1 последовательность (6) бесконечно мала и

что доказывает четвертое утверждение теоремы 1.

4. Переход к пределу в неравенстве

Докажем теорему о правиле перехода к пределу в неравенстве.

Теорема 2. Пусть limn xn = l и limn yn = p и для всех натуральных n справедливы неравенства

xn yn.

Тогда l p.

Доказательство. Дадим логические определения пределов, упомянутых в формулировке теоремы 2,

> 0 n1 n > n1 xn l <

и

> 0 n2 n > n2 yn p < .

52

Желая выполнения обоих неравенств, обозначим n0 = max{n1, n2} и будем рассматривать n > n0. Теперь из тождества l p = (l xn) + (xn yn) + (yn p),

в правой части которого первая и третья скобки не превосходят , а вторая не превосходит нуля, следует,что l p < 2 .

Полагая, например, = (1/2)(1/(10n)), для любого натурального n получаем неравенство l p 101n .

По лемме 1 лекции 3 получаем l p 0, что доказывает теорему 2.

Лемма 1 лекции 3 является весьма частным случаем теоремы 2, так как 1/10n 0 при n .

Заметим, что условие теоремы 2 допускает ослабление в выполнении неравенства xn yn, которому достаточно быть справедливым не для всех натуральных n, а начиная с некоторого номера n0.

5. Сходимость последовательности, ограниченной двумя последовательностями с одинаковыми пределами

Сформулируем еще одну теорему о неравенствах, полезную во многих случаях.

Теорема 3. Пусть limn xn = limn zn = l и для всех натуральных n справедливы неравенства

xn yn zn.

Тогда limn yn = l.

53

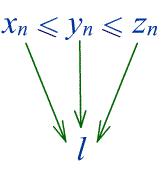
Рис. 1. Сходимость последовательности, ограниченной двумя последовательностями с одинаковыми пределами.

Теорема 3 известна своими фольклорными названиями. Так, в российском преподавании она слывет как теорема о двух милиционерах, а в англоязычных учебниках ей дают название теоремы о сэндвиче.

Доказательство. Дадим логические определения пределов, упомянутых в формулировке теоремы 3,

> 0 n1 n > n1 xn l <

и

> 0 n2 n > n2 zn l < .

Желая выполнения обоих неравенств, обозначим n0 = max{n1, n2} и будем рассматривать n > n0. Теперь из этих двух неравенств и соотношения xn yn zn выводим цепочку неравенств

< xn l yn l zn l < .

Выделяя среднее звено и два крайних, сформулируем результирующее предложение

> 0 n0 n > n0 yn l < ,

54

которое означает, что limn yn = l и доказывает теорему 3.

Аналогично предыдущим теоремам заметим, что условие теоремы 3 допускает ослабление в выполнении неравенств xn yn zn, которым достаточно быть справедливыми не для всех натуральных n, а начиная с некоторого номера n0.

55

Лекция 6

1. Подпоследовательность сходящейся последовательности

2. Частичные пределы последовательности

3. Существование верхнего предела ограниченной последовательности 4. Сходимость последовательности, имеющей равные верхний и нижний пределы

1. Подпоследовательность сходящейся последовательности

Сначала покажем, что все подпоследовательности сходящейся последовательности ведут себя похожим образом.

Теорема 1. Если последовательность сходится к пределу l, то любая ее подпоследовательность сходится к тому же пределу l.

Доказательство. Пусть limn xn = l. Это значит, что

> 0 n0 n > n0 xn l < .

Рассмотрим подпоследовательность xn1 , xn2 ,..., xnk ,... . Номера nk неограниченно возрастают при k , поэтому найдется номер k0 такой, что nk > n0 при k > k0. Соединяя вместе все сказанное, получаем логическое предложение

> 0 k0 k > k0 | xnk l | ,

которое служит определением того, что limk xnk l, и доказывает теорему 1.

2. Частичные пределы последовательности

Рассмотрим последовательность

56

(1) 1, 0, 1, 0, ..., 1, 0, ... .

Эта последовательность расходится. Не вдаваясь в подробное обсуждение, пообещаем вскоре получить критерий Коши, мгновенно подтверждающий расходимость последовательности (1). Тем не менее последовательность (1) имеет сходящиеся подпоследовательности

1, 1, ..., 1, ... и 0, 0, ..., 0, ... .

Первая из подпоследовательностей сходится к 1, вторая - к 0.

Пример (1) показывает, что расходящиеся последовательности могут иметь подпоследовательности, сходящиеся к различным пределам, которым дадим название частичных пределов.

Определение 1. Число l называется частичным пределом последовательности x1, x2, ..., xn, ..., если существует ее подпоследовательность, сходящаяся к l.

Множество X частичных пределов последовательности (1) состоит из двух элементов: 1 и 0. Нетрудно придумать иные примеры последовательностей с любым конечным и даже с бесконечным множеством частичных пределов.

Если множество X частичных пределов последовательности ограничено, то X имеет верхнюю и нижнюю грани, которым дадим специальные названия.

Определение 2. Наибольший из частичных пределов последовательности x1, x2, ..., xn, ... называется верхним пределом данной последовательности и обозначается limn xn или lim sup xn. Наименьший из частичных пределов последовательности x1, x2, ..., xn,

... называется нижним пределом данной последовательности и обозначается limn xn или lim inf xn.

3. Существование верхнего предела ограниченной последовательности

Докажем теорему существования верхнего предела ограниченной последовательности.

57

Теорема 2. Всякая ограниченная последовательность имеет верхний предел.

Доказательство. Пусть последовательность x1, x2, ..., xn, ... ограничена. Множество ее элементов и любое его подмножество имеет верхнюю грань. Обозначим

1 sup xn sup x1, x2 ,..., xn ,... ,

n 1

2 sup xn sup x2 , x3 ,..., xn ,... ,

n 2

..........................................................

k sup xn sup xk , xk 1,..., xn ,... ,

n k

...........................................................

Поскольку верхняя грань множества не меньше верхней грани его подмножества, между величинами k возникают неравенства

1 2 ... k ... .

58

Кроме того, k infn 1xn для любого натурального k. Значит, невозрастающая последовательность 1, 2, ..., k, ... ограничена снизу и поэтому сходится. Обозначим

limk k infk k .

1

Покажем, что limn xn . Для этого убедимся, во-первых, что является частичным пределом последовательности x1, x2, ..., xn, ..., а во-вторых, что любой другой частичный предел этой последовательности не превосходит .

Начнем с построения подпоследовательности, сходящейся к . Сначала выпишем свойства чисел k, k , как верхних граней соответствующих множеств.

1. n k xn k;

2. > 0 nk k xnk > k .

Положим = 1/k, соединим свойства 1-2 и получим

k 1 nk k k 1k xnk k .

59

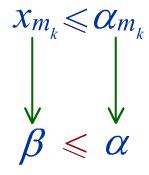
Рис. 1. Сходимость подпоследовательности xnk к . По теореме 3 лекции 5 заключаем, что последовательность

xn1 , xn2 ,..., xnk ,...

сходится к . Поскольку нет гарантии, что номера nk возрастают, то из последней последовательности выделим подпоследовательность с возрастающими номерами ее элементов. Тогда эта подпоследовательность является в то же время

подпоследовательностью исходной последовательности x1, x2, ..., xn, ... и сходится к . Таким образом, мы доказали, что оказывается частичным пределом исходной последовательности.

Теперь убедимся, что любой другой частичный предел исходной последовательности не превосходит . Действительно, пусть - частичный предел. Значит, из исходной последовательности можно выделить подпоследовательность

Рис. 2. Переход к пределу в неравенстве xmk mk .

60