Mat_Analiz_Prokhorov

Перемножив все неравенства, после многочисленных сокращений получим

или

Это нарушает необходимое условие limn an = 0 сходимости ряда. Следовательно, числовой ряд е an расходится, что заканчивает доказательство теоремы 4.

Случай l = 1 не попал в перечень возможностей, рассмотренных в теореме 4, и не имеет гарантированного ответа.

Во второй части теоремы 4 делается вывод о расходимости ряда е an , но доказательство в равной степени устанавливает и расходимость ряда еan.

Утверждение теоремы 4 охватывает и случай l = , в котором ряд е an расходится.

81

5. Признак Коши для рядов с убывающими слагаемыми

Продолжим перечень употребительных признаков сходимости числовых рядов признаком Коши для рядов с убывающими слагаемыми, который будет позднее усилен интегральным признаком Коши, но на первоначальном этапе изучения рядов позволит исследовать несколько принципиально важных примеров.

Теорема 5. Пусть a1 a2 ... an ... 0. Тогда ряды

сходятся или расходятся одновременно.

Доказательство. Из условий теоремы 5 вытекает, что для k = 2n 1, 2n 1+1, ..., 2n 1 справедливы неравенства a2n ak a2n 1 .

Суммируя эти 2n 1 неравенств по всем k = 2n 1, 2n 1+1, ..., 2n 1, находим

2n 1

2n 1 a2n е ak 2n 1 a2n 1 . k 2n 1

Суммируем последние неравенства по n = 1, 2, ..., m и получим

82

p

Sp еan

n 1

- частная сумма ряда еan, а

p

p е2n a2n

n 1

- частная сумм ряда 2n a2n . Тогда неравенства (4) интерпретируются как

Первое неравенство в (5) означает, что если частные суммы Sn ограничены, то и частные суммы n ограничены, и по теореме 5 лекции 7 из сходимости ряда еan следует сходимость ряда

Второе неравенство в (5) означает, что если частные суммы n ограничены, то и частные суммы S2n 1 ограничены. Но частные

суммы Sn образуют неубывающую последовательность. Значит, для любого натурального p найдется число n такое, что p 2n 1 и поэтому

Sp S2n 1.

Следовательно, все частные суммы Sp ограничены, и по теореме 5 лекции 7 из сходимости ряда 2n a2n следует сходимость ряда еan, что доказывает теорему 5.

Пример. Рассмотрим числовой ряд

83

е1n 1 12 13 1n

иприменим теорему 5 для исследования его сходимости. Согласно этой теореме наш ряд сходится или расходится одновременно с рядом

е2n 21n е1 1 1 1 1 ,

который, очевидно, расходится. Следовательно, ряд е(1/n) расходится.

Ряд е(1/n) называется гармоническим рядом. Наше исследование показало, что гармонический ряд расходится.

84

Лекция 9

1. Абсолютная и условная сходимость числового ряда

2. Преобразование Абеля

3. Признак Дирихле сходимости числового ряда

4. Признак Абеля сходимости числового ряда

5. Признак Лейбница сходимости числового ряда

1. Абсолютная и условная сходимость числового ряда

Все признаки сходимости лекции 8 относились к числовым рядам е an . Этот феномен не случаен, дадим ему отдельное название.

Определение 1. Числовой ряд еan называется абсолютно сходящимся, если сходится ряд е an .

В определении 1 ничего не говорится о сходимости самого ряда еan. Тем не менее сходимость нашего ряда подразумевается, потому что абсолютная сходимость влечет сходимость ряда, в чем мы сейчас убедимся. Сначала введем понятие положительной и отрицательной части числа.

Определение 2. Пусть a . Число

называется положительной частью числа a, а число

85

Очевидны соотношения между a, a , a+ и a :

Теорема 1. Если числовой ряд еan абсолютно сходится, то он сходится.Этот ряд абсолютно сходится тогда и только тогда, когда сходятся ряды еan+ и еan .

Доказательство. По существу в теореме 1 высказаны два утверждения. Начнем со второго из них, которое имеет характер необходимого и достаточного условия абсолютной сходимости ряда.

Пусть ряд еan абсолютно сходится. Значит, сходится ряд е an . Из неравенств

по признаку мажорации следует сходимость рядов еan+ и еan , что доказывает необходимость условия во второй части теоремы 1. Попутно отметим, что

Обратно, пусть ряды еan+ и еan сходятся. Тогда справедливы соотношения (1) между частными суммами рассматриваемых рядов,

из которых следует сходимость рядов е an и еan и справедливость формул (2). Это доказывает достаточность условия во второй части теоремы 1.

86

Одновременно, принимая во внимание абсолютную сходимость нашего ряда, мы доказали первое утверждение и завершили доказательство теоремы 1.

Дадим название сходимости, альтернативной абсолютной сходимости.

Определение 2. Числовой ряд еan называется условно сходящимся, если он сходится, но не сходится абсолютно.

Теорема 1 имеет свою собственную альтернативу, исходящую из первой формулы в (1). Если сумма двух последовательностей сходится, то либо обе складываемые последовательности сходятся, либо обе они расходятся. Это приводит нас к утверждению:

если ряд еan условно сходится, то оба ряда еan+ и еan расходятся.

2. Преобразование Абеля

В признаках сходимости рядов полезна следующая формула, называемая преобразованием Абеля.

Доказательство. Принимая во внимание очевидные формулы b1 = B1, b2 = B2 B1, ..., bn = Bn Bn 1,

получим

87

B1(a1 a2) + B2(a2 a3) + ... + Bn 1(an 1 an) + Bnan =

n 1

е Bk ak ak 1 Bn an ,

k 1

что эквивалентно формуле в лемме 1 и заканчивает ее доказательство.

3. Признак Дирихле сходимости числового ряда

Пользуясь преобразованием Абеля, выведем признаки сходимости числовых рядов, которые способны установить как абсолютную, так и условную сходимость. Следующий признак принадлежит Дирихле.

Теорема 2. Предположим, что выполняются следующие условия:

n

1. последовательность частных сумм Bn еbk ограничена;

k1

2.последовательность a1, a2, ..., an, ... монотонна и limn an = 0.

Тогда числовой ряд еanbn сходится

Доказательство. Последовательность чисел anBn, n = 1, 2, ..., бесконечно мала как произведение бесконечно малых an и ограниченных Bn. Преобразование Абеля гарантирует в таком случае одновременную сходимость или расходимость рядов

еanbn и е(an+1 an)Bn. Применим критерий Коши к исследованию сходимости второго из этих рядов.

Пусть Bk M, k 1. Кроме того, запишем определение сходимости an к 0

88

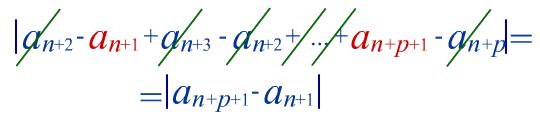
> 0 n0 n > n0 an < .

Теперь при n > n0 найдем оценку

Так как последовательность a1, a2, ..., an, ... монотонна, то числа ak+1 ak, k 1, не меняют знака с изменением k и поэтому

an+2 an+1 + an+3 an+2 + ... + an+p+1 an+p = an+p+1 an+1

an+p+1 + an+1 < + = 2 .

89

Рис. 1. Иллюстрация к признаку Абеля сходимости числового ряда. Соединяя все оценки вместе, убеждаемся, что

что эквивалентно по критерию Коши сходимости ряда е(an+1 an)Bn, а значит, и ряда еanbn. Теорема 2 доказана.

4. Признак Абеля сходимости числового ряда

В следующей теореме сформулируем признак Абеля, родственный признаку Дирихле и по математическому смыслу, и по способу доказательства.

Теорема 3. Предположим, что выполняются следующие условия:

1.числовой ряд еbn сходится;

2.последовательность a1, a2, ..., an, ... монотонна и ограничена.

Тогда числовой ряд еanbn сходится.

Доказательство. Пусть ak M, k 1. Кроме того, запишем критерий Коши сходимости ряда еbn

n p

Обозначим Bpn е bk . В этих обозначениях последнее неравенство примет вид

k n 1

90