Mat_Analiz_Prokhorov

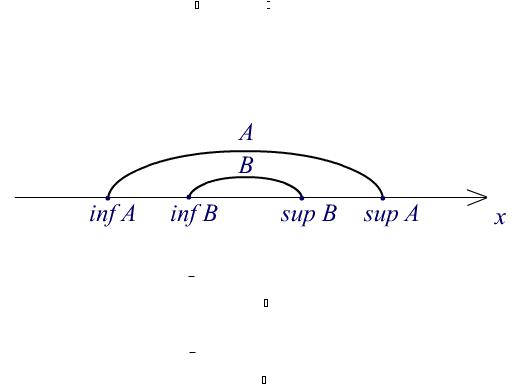
что равносильно второй формуле из утверждения теоремы 1 и заканчивает доказательство теоремы 1.

2. Монотонность интеграла Римана

Монотонность интеграла Римана выражается следующей теоремой.

Теорема 2. Пусть функции f и g интегрируемы по Риману и для всех x выполняется неравенство f(x) g(x).Тогда справедливо неравенство

f (x)dx g(x)dx.

Доказательство. В действительности, свойством монотонности обладает верхний интеграл, а следовательно, и интеграл

Римана. Прежде всего заметим, что неравенство f(x) g(x) влечет условие соотношения между множествами ступенчатых функций

{fст: fст f} {fст: fст g}.

Рис. 1. Иллюстрация к доказательству монотонности интеграла Римана.

Нижняя грань

I( f ) finff fст (x)dx

ст

большего множества не превышает нижней грани

I(g) finfg fст (x)dx

ст

его подмножества, то есть

I(f) I(g),

что влечет утверждение теоремы 2 и заканчивает его доказательство.

231

3. Аддитивность интеграла Римана

Определим интеграл Римана по множеству E.

Определение 1. Финитная ограниченная функция f называется интегрируемой по Риману на множестве E, если

произведение f E интегрируемо по Риману. В этом случае интеграл Римана от функции f E называется интегралом Римана от функции f на множестве E и обозначается

f (x)dx.

E

Таким образом,

f (x)dx ( f E )(x)dx.

EE

Определение 1 может быть отнесено и к функциям, заданным только на множестве E.

В частности, если множество E является одним из промежутков [a, b], [a, b), (a, b] или (a, b), то интеграл от функции f на множестве E обозначается

b

f (x)dx.

a

Следующая теорема выражает свойство аддитивности интеграла Римана.

Теорема 3. Если функция f интегрируема по Риману на взаимно непересекающихся множествах E1 и E2, то f интегрируема на объединении E = E1 E2 и справедлива формула

f (x)dx f (x)dx f (x)dx.

EE1 E2

Доказательство. Интегрируемость функции f на множествах E1 и E2 означает, что функции f E1 и f E2 интегрируемы по Риману. Так как E1 и E2 взаимно не пересекаются, то

E1 E2 = E1 + E2.

232

Следовательно, функция f E интегрируема по Риману, что означает интегрируемость функции f на множестве E и заканчивает доказательство теоремы 3.

4. Интегрируемость модуля интегрируемой функции

Покажем, что модуль интегрируемой функции также является интегрируемой функцией.

Теорема 4. Пусть функция f интегрируема по Риману. Тогда функция f также интегрируема по Риману и справедливо неравенство

f (x)dx f (x) dx.

Доказательство. Интегрируемость функции f означает равенствоI(f) = I(f).

По свойству верхней грани в определении нижнего интеграла

I( f ) sup fст (x)dx

f ст f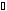

для всякого > 0 найдется ступенчатая функция f1 f такая, что

Вычитая неравенство (1) из неравенства (2), видим, что

233

Положительные части f1+ и f2+ ступенчатых функций f1 и f2 остаются ступенчатыми функциями, при этом сохраняются неравенства

f1+ f+ f2+.

Покажем, что

Таким образом, неравенство (3) проверено во всех возможных случаях соотношений между f1, f2, f1+ и f2+. Теперь произведем оценки нижнего и верхнего интегралов от функции f+

Вычитая неравенство (4) из неравенства (5), видим, что

I( f ) I( f ) f2 (x)dx f1 (x)dx

234

( f2 f1 )(x)dx ( f2 f1 )(x)dx 2 .

Осталось в этом неравенстве перейти к пределу при 0, чтобы получить неравенствоI(f) I(f) 0,

в котором возможен только знак равенства

I(f) I(f) = 0,

что доказывает интегрируемость функции f+.

Применяя те же рассуждения к функции ( f), приходим к утверждению об интегрируемости функции ( f)+ = f . Вместе эти два свойства дают интегрируемость функции

f = f+ + f .

Пользуясь монотонностью и линейностью интеграла Римана и неравенствами

получаем, что

что равносильно неравенству

f (x)dx f (x)dx

и заканчивает доказательство теоремы 4.

235

Лекция 23.

1. Интегральные суммы Римана

2. Критерий интегрируемости функции по Риману

1. Интегральные суммы Римана

Вернемся к геометрическому подходу в теории интеграла Римана. Конструкция нижнего и верхнего интегралов вдохновлялась идеей достижения верхней грани сумм площадей прямоугольников, вписанных в криволинейную трапецию, и нижней грани сумм площадей прямоугольников, описанных около криволинейной трапеции.

Промежуточное положение прямоугольников возникает в случае пересечения их верхних сторон с графиком функции.

Рис. 1. Геометрическое представление интеграла Римана

236

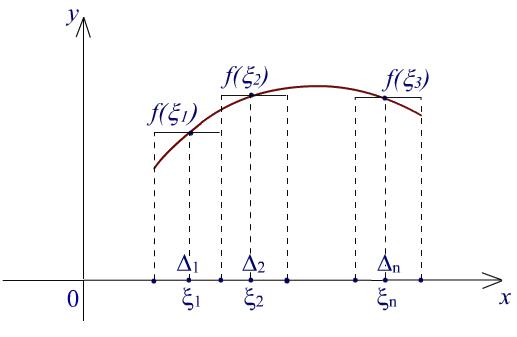
Аналитически пересечение ступеньки с графиком функции f означает, что высота ступеньки равна значению f( ) функции f в некоторой точке . Набор ступенек над отрезком [a, b] предполагает разбиение отрезка [a, b] на части.

Определение 1. Набор P = {x0, x1, x2, ..., xn 1, xn} точек a = x0 < x1 < x2 < ... < xn 1 < xn = b называется разбиением отрезка [a, b].

Рис. 2. Разбиение отрезка

Имея разбиение отрезка [a, b], мы представим [a, b] как объединение отрезков k = [xk 1, xk], k = 1, 2, ..., n, [a, b] = k=1n k.

Эти отрезки попарно не пересекаются, за исключением точек деления x1, x2, ..., xn 1, которые являются крайними точками двух соседних отрезков.

Метрической характеристикой разбиения служит максимальная длина отрезков k.

Определение 2. Пусть P = {x0, x1, x2, ..., xn 1, xn} - разбиение отрезка [a, b]. Тогда число

= max1 k n (xk xk 1)

называется диаметром разбиения P. Будем обозначать диаметр разбиения символом diam P.

Реализуем геометрическую идею построения промежуточных прямоугольников в следующем аналитическом определении.

Определение 3. Пусть дано разбиение P = {x0, x1, x2, ..., xn 1, xn} отрезка [a, b] и набор = { 1, 2, ..., n} точек k k, k = [xk 1, xk], k = 1, 2, ..., n. Если функция f определена на отрезке [a, b], то сумма

n

S(P, ; f ) е f ( k ) k ,

k 1

где k = xk xk 1, k = 1, 2, ..., n, называется интегральной суммой функции f, соответствующей разбиению P и набору .

237

В обозначении указано, что интегральная сумма функции f зависит от разбиения P и набора точек . Можно ожидать, что для интегрируемой функции f интегральная сумма приближается к интегралу от функции f при некотором процессе

регулирования разбиения P или набора . Мы увидим в дальнейшем, что вполне достаточно делать разбиение бесконечно мелким независимо от выбранного набора точек .

Другими словами, мы намереваемся найти предел интегральной суммы при диаметре разбиения, стремящемся к нулю. Сначала опишем такой предельный переход, опираясь на стандартное понятие предела функции S, зависящей от диаметра

разбиения . Поскольку > 0, то по существу мы опишем односторонний предел при +0.

Пусть P - разбиение отрезка [a, b] и = diam P. Тогда число I является пределом интегральной суммы при 0, I = lim 0S (P, ; f), если

> 0 > 0 P 0 < < S(P, ; f) I < .

Разумеется, функция f в процессе предельного перехода считается заданной, зато разбиение отрезка [a, b] и набор меняются. При этом конкретный выбор точек разбиения оказывается несущественным, как и выбор точек набора , а важной оказывается лишь бесконечная малость диаметра .

2. Критерий интегрируемости функции по Риману

Покажем, что возможность предельного перехода в интегральной сумме при диаметре разбиения, стремящемся к нулю, равносильна интегрируемости по Риману функции f.

Теорема 1. Функция f интегрируема по Риману на отрезке [a, b] тогда и только тогда, когда ее интегральные суммы, соответствующие разбиениям [a, b], имеют предел при диаметре разбиения , стремящемся к нулю, независимо от выбора

конкретного разбиения и от набора точек . В этом случае предел I интегральных сумм равен интегралу Римана от функции f на отрезке [a, b]

b

I lim S(P, ; f ) f (x)dx.

0

a

Доказательство. Теорема 1 выражает необходимое и достаточное условие интегрируемости функции f через свойство ее интегральных сумм.

238

Начнем с доказательства необходимости утверждения. Пусть функция f интегрируема на отрезке [a, b]. Покажем, что ее интегральные суммы имеют предел при 0.

Интегрируемая функция f ограничена, что означает выполнение неравенства f(x) M на отрезке [a, b] с некоторым M. Интегрируемость функции f на отрезке [a, b] равносильна интегрируемости функции f [a, b]. Не ограничивая общности, будем считать, что f = 0 вне [a, b], иначе f [a, b] переобозначим через f. По определению интегрируемости имеем равенства

с непересекающимися промежутками 1 , 2 , ..., m .

239

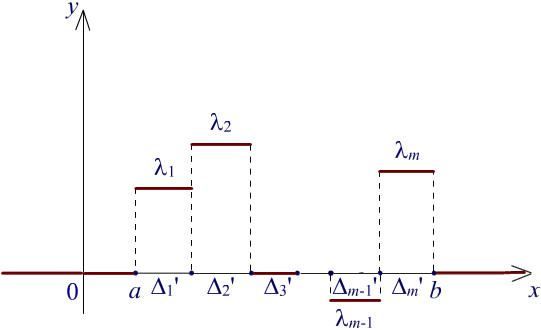
Рис. 3. Функция f1 = е m j=1 j j.

Можно считать, что все коэффициенты 1, 2, ..., m не превосходят M, в противном случае заменим на M те из

коэффициентов, которые превосходят M, с сохранением неравенств (1) и f1 f для измененной функции f1. Кроме того, можно считать, что

m j ' [a,b],

j 1

в противном случае заменим все j на j [a, b], а часть отрезка [a, b], непокрытую объединением промежутков j , представим в виде объединения конечного числа промежутков, чьи характеристические функции внесем в сумму (2) с нулевыми коэффициентами.

Если среди 1 , 2 , ..., m обнаружатся отрезки, вырожденные в точку, то мы расширим их до невырожденных отрезков. Действительно, пусть отрезки j1 , j2 , ..., jp вырождаются в точки c1, c2, ..., cp соответственно. Каждый из них граничит с некоторым соседним промежутком. Предположим, что j1 = {c1} граничит, например, с j = (c1, xj ). Выберем в j точку c1 , c1 c1 = 1, где 1 < /p, и заменим

240