сходится тогда и только тогда, когда интеграл F с переменным верхним пределом интегрирования, задаваемый формулой (1), является ограниченной функцией на полуоси [a, ).
3. Абсолютная сходимость несобственного интеграла Римана
По аналогии с теорией числовых рядов дадим определение абсолютной сходимости несобственного интеграла Римана.
Определение 1 Несобственный интеграл Римана от функции f на полуоси [a, ) называется абсолютно сходящимся, если сходится несобственный интеграл Римана от функции f на полуоси [a, ).
В соответствии с аналогичной теоремой для числовых рядов покажем, что абсолютная сходимость влечет сходимость несобственного интеграла.
Теорема 3 Если несобственный интеграл Римана
f (x)dx
a
абсолютно сходится, то он сходится.
Доказательство. Абсолютная сходимость несобственного интеграла Римана в теореме 3 означает сходимость несобственного интеграла Римана
f (x) dx.
a
Согласно критерию Коши выполняется условие
b''
> 0 b > a b',b''b'> b и b'' > b' f (x)dx .
b '
Знак модуля интеграла опущен, потому что f 0. Из этого условия выводим условие для исследуемого несобственного интеграла Римана
> 0 b > a b',b''b'> b и b'' > b' |
b'' |
f (x)dx |
b '' |
|
f (x)dx |
|
, |
|
|
|
b' |
|
b' |
|
|
|
|
которое является условием критерия Коши сходимости несобственного интеграла Римана. Следовательно, несобственный интеграл Римана от функции f на полуоси [a, ) сходится, что заканчивает доказательство теоремы 3.
4. Признак мажорации сходимости несобственных интегралов Римана
Связь между несобственными интегралами и числовыми рядами не только внешняя, но и весьма глубокая по содержанию, проблематике, средствам исследования и идейному наполнению.
Как и в теории числовых рядов, одна из основных задач теории несобственных интегралов состоит в выяснении сходимости или расходимости интегралов и в меньшей степени в их вычислении. Поэтому важную роль приобретают признаки сходимости - достаточные условия, допускающие относительно простую проверку. По аналогии с числовыми рядами начнем с признака мажорации.
Теорема 4 Пусть при фиксированном a и любом b > a функции f и g интегрируемы по Риману на отрезке [a, b] и для всех x a выполняется неравенство f(x) Cg(x) с некоторым C 0. Тогда сходимость несобственного интеграла Римана
g(x)dx
a
влечет абсолютную сходимость несобственного интеграла Римана
f (x)dx.
a
Доказательство. Для функции g, несобственный интеграл Римана которой сходится, согласно критерию Коши выполняется условие
> 0 b > a b',b''b'> b и b'' > b' |
b'' |
g(x)dx |
. |
|
b' |
|
|
Знак модуля интеграла здесь излишен, так как g 0 на полуоси [a, ). Пользуясь неравенством условия теоремы 4, получаем условие
> 0 b > a b',b''b'> b и b'' > b' b'' |
|
f (x) |
|
dx b'' Cg(x)dx C , |
|
|
b ' |
|
|
|
b' |
что равносильно критерию Коши сходимости несобственного интеграла Римана
f (x)dx .
a
Следовательно, несобственный интеграл Римана от функции f абсолютно сходится на полуоси [a, ), что заканчивает доказательство теоремы 4.
Заметим, что неравенство f(x) Cg(x) использовалось в условии критерия Коши не на всей полуоси [a, ), а только для x >
b. Таким образом, условие теоремы 4 можно ослабить, потребовав, чтобы нашлось b > a такое, что неравенство f(x) Cg(x) выполняется для всех x > b.
5. Признак сравнения сходимости несобственных интегралов Римана
Другое достаточное условие сходимости несобственного интеграла Римана называется признаком сравнения и дается в следующей теореме.
Теорема 5 Пусть при фиксированном a и любом b > a функции f и g интегрируемы по Риману на отрезке [a, b] и существует предел
Если l > 0, то несобственные интегралы Римана
одновременно абсолютно сходятся или не сходятся абсолютно. Если l = 0, то абсолютная сходимость второго из перечисленных интегралов влечет абсолютную сходимость первого интеграла.
Доказательство. По определению предела функции в точке x0 =
> 0 b x x > b |
|
|
|
|
f (x) |
|
|
l |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g(x) |
|
|
|
|
|
Это влечет неравенства
из которых заключаем, что для всех x > b выполняется неравенство
f (x) l g(x) .
Согласно признаку мажорации абсолютная сходимость несобственного интеграла Римана
a
влечет абсолютную сходимость несобственного интеграла Римана
a
что, в частности при l = 0, доказывает второе утверждение теоремы 5.
Если l = 0, то положив = l, из левого неравенства в формуле (3) выводим, что f(x) > 0 для x > b. Для таких x дробь g(x) / f (x) определена и существует предел
Применяя к паре функций f и g рассуждения первой части доказательства с заменой числа l на 1/l, заключаем, что абсолютная сходимость несобственного интеграла Римана (5) влечет абсолютную сходимость несобственного интеграла Римана (4), что заканчивает доказательство теоремы 5.
Если принять, что предел в теореме 5 бесконечен,
то меняя ролями функции f и g, сводим исследование к случаю l = 0. Таким образом, добавим к теореме 5 утверждение: если при условиях теоремы 5 выполняется условие (6), то абсолютная сходимость несобственного интеграла Римана (5) влечет абсолютную сходимость несобственного интеграла Римана (4).
Признаки мажорации и сравнения рассчитаны на то, что исследуемая функция f сравнивается с некоторой тестовой функцией g, о которой известно поведение ее несобственного интеграла Римана. Естественно, что набор тестовых функций должен, в первую очередь, состоять из простейших, например, степенных функций.
Пример 1. Пусть a = 1 и g(x) 1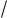
x p . Если p = 1, то одной из первообразных функции g является G(x) = log x. Если p 1, то одной из первообразных функции g является G(x) = 1/(p 1)xp 1. Вычислим
b |
b |
1 |
|
|
|
|
|
|
1 |
|
|
|
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p 1 |
g(x)dx |
|
|
|
|
p |
1 b |
|
|
x |
p |
|
|
|
1 |
1 |
|
|
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
logb, p 1. |
Если p > 1, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
0 . |
|
|
|
|
|
b p 1 |
|
|
|
|
|
b |
|
|
|
|
|
|
|
Если же p < 1, то limb b p 1 = 0, а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
1 |
|
|
|
|
|
|
|
|
bp 1 |
|
|
|
|
|
|
|
b |
|
|
|
не существует. Наконец, если p = 1, то limb log b также не существует. Подводя итог, заключаем, что
lim b 1p dx
b 1 x
существует и равен 1/(p 1), если p > 1, и не существует, если p 1. Следовательно, несобственный интеграл Римана
1 dx
1 xp
сходится, если p > 1, и расходится, если p 1.
Следствие Пусть при фиксированном a и любом b > a функция f интегрируема по Риману на отрезке [a, b] и существует предел
lim f (x) x p l .
x
Тогда несобственный интеграл Римана
f (x)dx
a
абсолютно сходится, если p > 1, и не сходится абсолютно, если l > 0 и p 1.
Доказательство следствия основано на применении признака сравнения, в котором g(x) = 1/xp.
Лекция 29.
1. Интегральный признак Коши сходимости числовых рядов
2. Условная сходимость несобственного интеграла Римана
3. Признак Дирихле сходимости несобственных интегралов Римана
4. Признак Абеля сходимости несобственных интегралов Римана
1. Интегральный признак Коши сходимости числовых рядов
Развивая аналогии между теорией числовых рядов и несобственных интегралов, докажем интегральный признак Коши, устанавливающий одновременную сходимость несобственного интеграла и соответствующего числового ряда.
Теорема 1 Пусть функция f монотонна на полуоси [1, ). Числовой ряд
сходится или расходится одновремнно с несобственным интегралом Римана
Доказательство. Докажем теорему 1 для невозрастающей функции f. Случай неубывающей функции f сводится к рассматриваемому случаю переходом к функции f.
Невозрастающая функция f имеет предел, конечный или бесконечный, при x . Сначала покажем, что если limx f(x) 0, то числовой ряд (1) и несобственный интеграл Римана (2) расходятся. Действительно, условие limn f(n) 0 противоречит необходимому условия сходимости ряда (1) и доказывает его расходимость. Обозначим limx f(x) = l. Если l > 0, то f(x) l для всех x 1. Предположение, что несобственный интеграл Римана (2) сходится, по признаку мажорации приводит к
утверждению, что несобственный интеграл Римана от функции y = l сходится на полуоси [1, ), что противоречит очевидному факту. Если l < 0, то по определению предела
> 0 b x x > b f(x) l < .
Из последнего неравенства находим, что f(x) < l + . Положив = l/2, получаем, что f(x) < l/2 или f(x) > l/2 для всех x > b. Предположение, что несобственный интеграл Римана (2) сходится, по признаку мажорации приводит к утверждению, что
несобственный интеграл Римана от функции y = l/2 сходится на полуоси [1, ), что противоречит очевидному факту.
Пусть теперь limx f(x) = 0. Так как f не возрастает, то f(x) 0, x 1, и |
|
f(n) f(x) f(n + 1), |
n x n + 1, n = 1, 2, ... . |
|
Составим ступенчатые функции |
|
|
n |
n |
|
f1n е f (k 1) [n ,n 1) и f2n |
е f (k) [n,n 1) . |
|
k 1 |
k 1 |
Очевидно, что |
|
|
f1n(x) f(x) f2n(x), |
1 x < n + 1. |
|
Рис. 1. Иллюстрация к доказательству теоремы об |
Рис. 2. Иллюстрация к доказательству теоремы об |
интегральном признаке Коши |
интегральном признаке Коши |
Предположим, что числовой ряд (1) сходится и |
|
|
|
|
е f (n) S. |
|
n 1 |
Для каждого b > 1 найдется натуральное число n > b. Оценим
b |
n |
n |
n 1 |
|
F(b) f (x)dx f (x)dx f2 (n 1) (x)dx е f (k ) е f (k) S. |
1 |
1 |
a |
k 1 |
k 1 |
что означает ограниченность функции y = F(b). По критерию сходимости несобственных интегралов Римана от неотрицательной функции f несобственный интеграл (2) сходится.
Обратно, пусть несобственный интеграл Римана (2) сходится и
|
|
|
|
|
|
f (x)dx I. |
|
|
1 |
|
|
|
Оценим частные суммы числового ряда (1) |
|
|
|
|
n |
n |
|
n 1 |
n |
Sn е f (k ) f (1) |
е f (k) f (1) |
е f (k 1) |
f (1) f1n (x)dx |
k 1 |
k 2 |
|
k 1 |
1 |
|
n |
|
|
|
f (1) f (x)dx |
f (1) f (x)dx f (1) I. |
|
1 |
|
1 |
|
что означает ограниченность частных сумм Sn. По критерию сходимости числовых рядов с неотрицательными слагаемыми числовой ряд (1) сходится, что заканчивает доказательство теоремы 1.
Теорема 1 усиливает теорему 5 лекции 8. В лекции 8 было показано, что гармонический ряд
|
|
|
|
|
|
|
|
|
е 1 |
1 |
1 |
|
1 |
... |
1 |
... |
n 1 |
n |
|
2 |
|
3 |
|
n |
|
расходится. Тот же факт мгновенно следует из теоремы 1, потому что несобственный интеграл Римана
1 dx
1 x
расходится.
2. Условная сходимость несобственного интеграла Римана
Сходящиеся несобственные интегралы Римана либо абсолютно сходятся, либо не сходятся абсолютно.
Определение 1 Несобственный интеграл Римана называется условно сходящимся, если он сходится, но не сходится абсолютно.
Иными словами, несобственный интеграл Римана
