Mat_Analiz_Prokhorov

151

Непосредственными арифметическими действиями проверяем, что

lim (x) 0,

x x0

то есть функция бесконечно мала при x x0. Так как

Ag(x0 ) Bf (x0 )

g2 (x0 )

-число, то равенство (6) определяет f/g как дифференцируемую в точке x0 функцию, причем

что доказывает четвертую часть теоремы 1 и завершает ее доказательство.

2. Дифференцируемость сложной функции

Покажем, что помимо арифметических действий, свойство дифференцируемости функции инвариантно относительно композиции, и выведем формулу производной сложной функции.

Теорема 2. Пусть функция y = f(x) дифференцируема в точке x0, а функция z = g(y) дифференцируема в точке y0, y0 = f(x0). Тогда сложная функция z = g(f(x)) дифференцируема в точке x0 и справедлива формула

(g(f)) (x0) = g (y0)f (x0).

Доказательство. Существование сложной функции при условиях теоремы 2 мы обсудили ранее в доказательстве теоремы о непрерывности сложной функции. Рассуждения сохраняют силу, так как обе функции f и g непрерывны в точке x0.

152

Так как функция f дифференцируема в точке x0, а функция g дифференцируема в точке y0, то существуют числа A и B и бесконечно малая при x x0 функция = (x) и бесконечно малая при y y0 функция = (y) такие, что справедливы формулы

(1) f(x) = f(x0) + A(x x0) + (x)(x x0)

и

(7) g(y) = g(y0) + B(y y0) + (y)(y y0), где A = f (x0) и B = g (y0).

Полагая y = f(x), подставим выражение (1) в равенство (7) и получим

(8) g(f(x)) = g(f(x0)) + B(A(x x0) + (x)(x x0)) + (f(x))(A(x x0) + (x)(x x0)).

Строго говоря, функция z = (f(x)) не вполне определена, поскольку функция z = (y) не определена в точке y0. Исправим этот недостаток, положив

(y0) = 0.

При таком доопределении функция z = (y) становится непрерывной в точке y0, так как limy y0 (y) = 0 = (y0).

Более того, сложная функция z = (f(x)) непрерывна и бесконечно мала в точке x0 как композиция непрерывной и бесконечно малой в точке y0 функции z = (y) и непрерывной и бесконечно малой в точке x0 функции y = f(x), y0 = f(x0).

Обозначим

(x) = B (x) + (f(x))(A + (x))

153

и перепишем равенство (8) в форме

g(f(x)) = g(f(x0)) + BA(x x0) + (x)(x x0).

Прямой проверкой убеждаемся, что limx x0 (x) = 0, то есть функция бесконечно мала при x x0. Так как BA - число, то последнее равенство определяет композицию g°f как дифференцируемую в точке x0 функцию, причем

(g(f)) (x0) = BA = g (y0)f (x0),

что завершает доказательство теоремы 2.

3. Производная обратной функции

Выведем формулу производной обратной функции при условии, что обратная функция существует.

Теорема 3. Пусть функция y = f(x) дифференцируема в точке x0, f (x0) 0, и имеет обратную функцию x = f 1(y). Тогда обратная функция дифференцируема в точке y0, y0 = f(x0), и справедлива формула

( f 1 )' (y0 ) f '(1x0 ) .

Доказательство. Функция f определена в -окрестности точки x0. Обозначим эту окрестность через X, а ее образ при отображении f - через Y. По доказанной в лекции 14 теореме функция f 1 непрерывна в точке y0.

Воспользуемся формулой

f '(x0 ) lim f (x) f (x0 ) .

154

Подставим сюда x = f 1(y) и заметим, что благодаря непрерывности функций y = f(x) в точке x0 и x = f 1(y) в точке y0 условие x x0 эквивалентно условию y y0

что устанавливает дифференцируемость обратной функции f 1 и требуемую формулу и заканчивает доказательство теоремы 3.

4. Локальный экстремум. Теорема Ферма

Дадим определение локального экстремума.

Определение 1. Говорят, что функция f имеет в точке x0 локальный минимум, если существует > 0 такое, что для всех x, x x0 < , выполняется неравенство

f(x) f(x0).

Аналогично функция f имеет в точке x0 локальный максимум, если существует > 0 такое, что для всех x, x x0 < , выполняется неравенство

f(x) f(x0).

Функция f имеет в точке x0 локальный экстремум, если она имеет в этой точке локальный минимум или локальный максимум.

155

Докажем замечательную теорему Ферма, выражающую необходимое условие локального экстремума дифференцируемой функции.

Теорема 4. Пусть функция f дифференцируема в точке x0 и имеет в этой точке локальный экстремум. Тогда справедливо равенство

f (x0) = 0.

Доказательство. Предположим, что функция f, дифференцируемая в точке x0, имеет в этой точке локальный максимум. В случае локального минимума рассуждения симметричны. Воспользуемся формулой

f '(x0 ) lim f (x) f (x0 ) .

Коль скоро предел написанного отношения существует, то существуют и равные ему односторонние пределы

156

Аналогично, если x0 < x < x0 + , то f(x) f(x0) 0 и x x0 > 0. Следовательно, для таких x

f (x) f (x0 ) 0 x x0

и поэтому

Формулы (9), (10) и (11) вместе приводят к заключению о равенстве

f (x0) = 0

и доказывают теорему 4.

Теорема 4 предлагает первый шаг в алгоритме решения задачи о поиске локального экстремума дифференцируемой функции. Согласно этой теореме первый отбор состоит в решении уравнения

f (x) = 0.

Точки локального экстремума могут находиться только среди корней этого уравнения, которые называются критическими точками функции f.

Теорема 4 имеет ясную геометрическую интерпретацию: график дифференцируемой функции в точке x0 локального экстремума имеет касательную, параллельную оси OX.

157

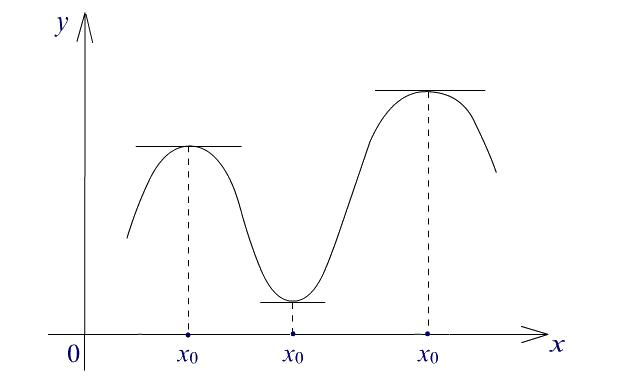
Рис. 1. Геометрическая иллюстрация теоремы Ферма.

Пример функции y = f(x) = x3 показывает, что не все критические точки непременно становятся точками локального экстремума. Действительно, уравнение

(x3) = 3x2 = 0

имеет единственный корень x = 0, но очевидно, что кубическая функция строго монотонна и потому не имеет локального экстремума ни в какой точке.

158

Лекция 16

1. Теорема Ролля о среднем значении

2. Теорема Лагранжа о среднем значении

3. Теорема Коши о среднем значении

4. Правило Лопиталя для отношения бесконечно малых

5. Правило Лопиталя для отношения бесконечно больших

1. Теорема Ролля о среднем значении

Начнем с естественного определения.

Определение 1. Функция f называется дифференцируемой на множестве X, если она дифференцируема в каждой точке этого множества.

Следующая теорема, принадлежащая Роллю, имеет ясный геометрический смысл, сходный с истолкованием теоремы Ферма.

Теорема 1. Пусть функция f удовлетворяет условиям:

1.непрерывна на отрезке [a, b];

2.дифференцируема на интервале (a, b);

3.f(a) = f(b).

Тогда существует точка c (a, b) такая, что f (c) = 0.

Доказательство. По второй теореме Вейерштрасса непрерывная на отрезке [a, b] функция f достигает своего минимума и максимума. Обозначим

159

Существуют точки x1,x2 [a, b] такие, что f(x1) = m и f(x2) = M.

Если m = M, то f(x) = m = M для всех x [a, b]. Значит, f принимает постоянное значение на [a, b] и f (x) = 0 на [a, b], что согласуется с утверждением теоремы 1.

Если m < M, то ввиду равенства f(a) = f(b) по крайней мере одна из точек x1 или x2 находится внутри (a, b).

160