
Mat_Analiz_Prokhorov
.pdfНе ограничивая общности, можем считать, что m > n, то есть m = n + p для некоторого натурального числа p. При таком соглашении проделаем простые преобразования
n |
m |
|
n |
n p |
|
m |
|
еak еak |
|
еak еak |
|
еak |
. |
||
k 1 |
k 1 |
|
k 1 |
k 1 |
|
k 1 |
|
Запишем преобразованное таким образом условие (3) и переформулируем критерий Коши для последовательностей как критерий Коши для рядов.
Теорема 3. Числовой ряд еan сходится тогда и только тогда, когда
|
|
|
|
n p |
|
(3) |
> 0 n0 |
n > n0 |
p 1 |
е ak |
. |
|
|
|
|
k n 1 |
|
Заметим, как и прежде, что число в неравенстве условия (3) можно заменить на C с некоторым C > 0.
Теорема 3 выражает необходимое и достаточное условие сходимости ряда. Если условие (3) ослабить, то оно сохранится как необходимое, но не обязательно останется достаточным условием сходимости ряда. Осуществим такое ослабление, потребовав,
чтобы неравенство в (3) выполнялось не для всех p 1, а лишь для одного значения p = 1. В этом случае условие (3) приобретет вид
> 0 n0 n > n0 an+1 < ,
и выражает по существу, что limn an = 0.
Итак, мы готовы сформулировать необходимое условие сходимости ряда в следующей теореме.
Теорема 4. Если числовой ряд еan сходится, то
71
lim an 0.
n
Перейдем к интерпретации в теории рядов теоремы о сходимости монотонной ограниченной последовательности, которую иначе можно сформулировать так: монотонная последовательность сходится тогда и только тогда, когда она ограничена.
Предположим, что все члены ряда еan не отрицательны: an 0, n 1. Сравним частные суммы Sn и Sn+1 этого ряда
n 1 |
n |
Sn 1 Sn еak еak an 1 0. |
|
k 1 |
k 1 |
Отсюда следует, что Sn Sn+1 для всех натуральных n. Значит, последовательность частных сумм монотонна, и мы готовы переформулировать критерий сходимости монотонной последовательности как соответствующий критерий сходимости рядов с неотрицательными членами.
Теорема 5. Предположим, что an 0 для всех натуральных n. Числовой ряд еan сходится тогда и только тогда, когда последовательность S1, S2, ..., Sn, ... его частных сумм ограничена.
72
Лекция 8
1. Признак мажорации сходимости числового ряда
2. Признак сравнения сходимости числового ряда
3. Признак Коши сходимости числового ряда
4. Признак Даламбера сходимости числового ряда
5. Признак Коши для рядов с убывающими слагаемыми
1. Признак мажорации сходимости числового ряда
Геометрический ряд устроен относительно просто и играет заметную роль в теории рядов. Удача состоит и в том, что удается вычислить сумму геометрического ряда. Подобная возможность предоставляется относительно редко. Основная проблематика в теории рядов заключается не в нахождении суммы ряда, а в установлении его сходимости или расходимости.
Некоторые признаки основаны на сравнении данного ряда с каким-либо тестовым рядом, о котором определенно известно, сходится он или нет. Простейшим из алгоритмов сравнения является признак мажорации, выраженный в следующей теореме.
Теорема 1. Пусть для всех натуральных n выполняются неравенства
an Cbn, C > 0.
Тогда из сходимости числового ряда еbn следует сходимость числового ряда е an .
Доказательство. Согласно критерию Коши сходимость ряда еbn эквивалентна условию
|
n p |
|
> 0 n0 n > n0 p 1 |
е bk |
. |
|
k n 1 |
|
73
Знак модуля в последнем неравенстве можно опустить, потому что, как следует из условия теоремы 1, bn 0, n 1.
Поскольку
n p |
|
n p |
|
|
||||
е |
|
ak |
|
е Cbk , |
|
|
||
|
|
|
|
|||||
k n 1 |
|
k n 1 |
|
|
||||
приходим к условию |
|
|
||||||
|
|
|
|
n p |
|
|
||
> 0 n0 n > n0 p 1 е |
|
ak |
|
C , |
||||
|
|
|||||||
k n 1
что равносильно сходимости ряда е an и доказывает теорему 1.
Обратим внимание, что неравенство an Cbn теоремы 1 применялось не для всех n, а начиная с номера n0. Поэтому условие
теоремы 1 допускает ослабление. Именно, достаточно потребовать, чтобы неравенства an Cbn выполнялись для всех n > n0, где n0 - некоторое натуральное число.
2. Признак сравнения сходимости числового ряда
Другой признак, где используется знание о некоем тестовом ряде, известен под названием признака сравнения. Сформулируем его в следующей теореме.
Теорема 2. Пусть bn 0, n 1, и существует предел
lim |
|
an |
|
l, |
l 0. |
|
|
|
|||||
|
b |
|
|
|||
n |
|
|
|
|
||
|
|
n |
|
|
|
|
74

Если l > 0, то числовые ряды е an и е bn сходятся или расходятся одновременно. Если l = 0, то из сходимости ряда е bn следует сходимость ряда е an .
Доказательство. Последовательность
|
|
a1 |
|
|
, |
|
|
a2 |
|
|
,..., |
|
|
an |
|
|
,... |
||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||||||||
|
|
b |
|
|
|
|
b |
2 |
|
|
|
|
|
b |
|
|
|||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
сходится, поэтому она ограничена:
|
|
an |
|
|
C, |
n 1, |
|
|
|
|
|||||
|
|
b |
|
|
|
||
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
для некоторого C > 0. Отсюда вытекает неравенство an C bn , которое по признаку мажорации устанавливает сходимость
числового ряда е an , если сходится ряд е bn . Это доказывает вторую часть теоремы при l = 0 и одностороннюю зависимость между сходимостью двух рядов при l > 0.
Пусть l > 0. Докажем обратную зависимость между сходимостью рядов. Числа an могут обращаться в нуль лишь для конечного набора номеров, иначе нашлась бы подпоследовательность
|
an1 |
|
, |
|
|
an2 |
|
,..., |
|
|
ank |
|
,..., |
|||||
|
|
|
|
|
|
|
|
|||||||||||
|
b |
n |
|
|
|
|
b |
n |
|
|
|
|
b |
|
|
|||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|||
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
k |
|
|
сходяшаяся к нулю, а это противоречит предположению l > 0. Поэтому существует n0 такое, что an 0 для n > n0. Теперь заключаем, что отношение
an
bn
75
определено для всех n > n0,
|
|
bn |
|
|
1 |
|
|
|
|
|
|||
lim |
|
|
|
|
|
, |
|
a |
|
l |
|||
n |
|
|
|
|||
|
|
n |
|
|
|
|
и поэтому ограничено:
|
bn |
|
|
n > n0 , |
|
|
|||
|
|
|
||
|
an |
|
C , |
|
|
|
|
|
с некоторым C > 0. Вновь по признаку мажорации неравенство bn C an , n > n0, устанавливает сходимость числового ряда е bn , если сходится ряд е an , и заканчивает доказательство теоремы 2.
Если принять, что предел в теореме 2 бесконечен,
(1) |
lim |
|
an |
|
, |
|
|
|
|||||
|
b |
|
|
|||
|
n |
|
|
|
||
|
|
|
n |
|
|
|
то меняя ролями an и bn, сводим исследование к случаю l = 0. Таким образом, добавим к теореме 2 утверждение: если выполняется условие (1), то сходимость числового ряда е an влечет сходимость ряда е bn .
3. Признак Коши сходимости числового ряда
Признаки мажорации и сравнения предполагают знание о поведении одного из двух обсуждаемых рядов. Таким тестовым рядом часто выступает геометрический ряд. Есть несколько популярных признаков, в которых сравнение с геометрическим рядом проявляется в более глубокой форме, скрытой в доказательстве, и не выражено явно в их формулировках. Один из весьма распространенных признаков этого типа связывают с именем Коши. Он дается в следующей теореме.
Теорема 3. Предположим, что
76

lim n an l .
n
Если l < 1, то числовой ряд е an сходится. Если l > 1, то ряд е an расходится.
Доказательство. Пусть сначала l < 1. Положим
k sup k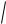
 ak , k 1 ak 1 ,..., n
ak , k 1 ak 1 ,..., n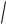
 an .
an .
Тогда
lim n an
n
и мы можем записать по определению
> 0 k0 k > k0 k l < .
Неравенство k l < равносильно системе двух неравенств
< k l < или
l < k < l + .
Следовательно, для всех k > k0 выполняется неравенство
k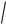
 ak
ak
limk k l
l .
Выберем > 0 таким, что l + < 1. Тогда из неравенстваak < (l + )k, k > k0,
и сходимости геометрического ряда е(l + )n по признаку мажорации выводим утверждение о сходимости числового ряда е an .
Пусть теперь l > 1. Верхний предел - это частичный предел. Значит, существует подпоследовательность
n1 an1 , n2
 an2 ,..., nk
an2 ,..., nk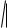 ank ,... ,
ank ,... ,
77

для которой
lim nk |
|
an |
k |
|
k |
|
Для этой подпоследовательности запишем по определению
> 0 k0 k > k0
Последнее неравенство равносильно системе двух неравенств
l nk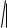 ank
ank
из которых, в частности, следует, что
|
an |
k |
|
> l nk , k > k0. |
|
|
Выберем > 0 таким, что l > 1. Тогда
an |
k |
> 1, k > k0 , |
|
|
|
|
l. |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
nk |
|
an |
|
|
l |
. |
|
|
|
|
|
||||||
|
|
|
|
|
k |
|
|
|
|
|
|
l , |
|
||||||
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
что нарушает необходимое условие limn an = 0 сходимости ряда. Следовательно, числовой ряд е an расходится, что заканчивает доказательство теоремы 3.
Случай l = 1 не попал в перечень возможностей, рассмотренных в теореме 3, и не имеет гарантированного ответа.
Во второй части теоремы 3 делается вывод о расходимости ряда е an , но доказательство в равной степени устанавливает и расходимость ряда еan.
Заметим, что утверждение теоремы 3 охватывает и случай l = , в котором ряд е an расходится.
4. Признак Даламбера сходимости числового ряда
Наряду с признаком Коши на практике очень удобен следующий признак Даламбера.
Теорема 4. Предположим, что an 0, n 1, и
78
lim |
|
|
an 1 |
|
l. |
||
|
|
|
|||||
|
|
||||||
|
|
|
a |
|
|
||
n |
|
|
|
|
|
||
|
|
|
|
n |
|
|
|
Если l < 1, то числовой ряд е an сходится. Если l > 1, то ряд е an расходится.
Доказательство. Пусть сначала l < 1. Запишем по определению
(2) |
> 0 n n > n |
|
|
an 1 |
|
|
l |
. |
|||
|
|
|
|
||||||||
|
|
||||||||||
|
|
|
|
|
|
||||||
0 |
0 |
|
|
|
an |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Последнее неравенство равносильно системе двух неравенств
(3) |
l |
|
an 1 |
|
|
l . |
||
|
|
|
||||||
|
|
|||||||
|
|
an |
|
|
|
|||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
Выберем > 0 таким, что l + < 1, и выпишем p последовательных неравенств
|
|
an 2 |
|
|
|
l |
||||||
|
|
|||||||||||
п |
|
|
|
|
0 |
|
|
|
|
|
||
|
|
an0 1 |
|
|
|
|
||||||
п |
|
|
|
|
|
|
||||||
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
an 3 |
|
|
|
|
|
||||||
п |
|
|
|
l |
||||||||
п |
|
|
|
|
0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||||
|
|
an 2 |
|
|
|
|||||||
|
|
|
|
|
|
|||||||
п |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
п.................. |
||||||||||||
п |
|
an0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||
п |
|
|
p 1 |
l . |
||||||||
п |
|
|
a |
n0 p |
|
|||||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|||||||
79
Перемножив все неравенства, после многочисленных сокращений получим
|
an0 p 1 |
l |
p |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
an0 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
an p 1 |
|
|
|
an 1 |
|
l |
p . |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сходимость геометрического ряда е |
|
an0 1 |
|
l p |
по признаку мажорации влечет сходимость числового ряда е |
|
an0 p 1 |
|
. Заметим, что |
|||||||||||||||
|
|
|
|
|||||||||||||||||||||
ряды |
и е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
е an |
|
an0 p 1 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
сходятся одновременно, так как их частные суммы отличаются на постоянное число
n0 1
е ak .
k 1
Таким образом, мы установили сходимость ряда е an .
Пусть теперь l > 1. Снова воспользуемся определением (2) с эквивалентной системой неравенств (3), выберем > 0 так, что l > 1, и выпишем p последовательных неравенств
80
