Mat_Analiz_Prokhorov

По определению Гейне, примененнному к результатам арифметических действий, заключаем, что функции f + g, f g, fg и f/g непрерывны в точке x0. Теорема 2 доказана.

Естественно, аналогичная теорема с подобным доказательством верна и для предела функции. Именно, если

В случае частного предполагаем дополнительно, что g(x) 0 и m 0.

4. Непрерывность сложной функции

Покажем, что понятие непрерывности инвариантно также относительно композиции.

Теорема 3. Пусть функция y = f(x) непрерывна в точке x0, а функция z = g(y) непрерывна в точке y0, y0 = f(x0). Тогда сложная функция z = g(f(x)) непрерывна в точке x0.

Доказательство. Сначала убедимся в том, что сложная функция определена в некоторой -окрестности точки x0. Действительно, функция g определена в некоторой -окрестности точки y0. Но определение Коши непрерывности функции f в точке x0 гарантирует существование -окрестности точки x0, которая при отображении f переходит в -окрестность точки y0.

111

Перейдем к непосредственному доказательству утверждения теоремы 3. Для этого воспользуемся определением непрерывности

по Гейне функции f в точке x0. Выберем произвольно последовательность точек x1, x2, ..., xn, ... из -окрестности точки x0 такую, что limn xn = x0. Тогда по определению Гейне

lim f xn f x0 .

n

Теперь воспользуемся определением непрерывности по Гейне функции g в точке y0 применительно к последовательности

Тогда

lim g yn g y0 .

n

Подставим в последнее соотношение yn = f(xn), y0 = f(x0) и придем к определению Гейне непрерывности сложной функции z = g(f (x)) в точке x0. Теорема 3 доказана.

5. Сохранение знака функции в окрестности точки непрерывности

Следующая теорема бывает полезной в различных задачах.

Теорема 4. Пусть функция f непрерывна в точке x0 и f(x0) 0. Тогда существует -окрестность точки x0, в которой значения f(x) не меняют знака.

112

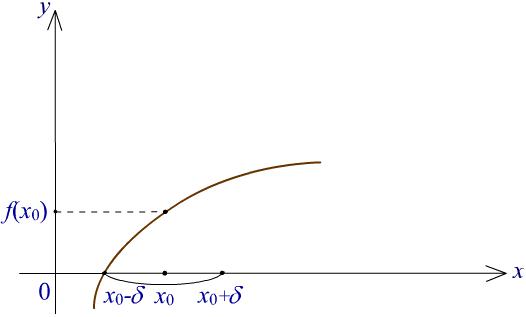
Рис. 2. Иллюстрация к теореме о сохранении знака функции в окрестности точки непрерывности. Доказательство. Остановимся на случае f(x0) > 0, справедливо полагая, что доказательство в случае f(x0) < 0 совершенно симметрично. Воспользуемся определением Коши непрерывности функции f в точке x0

> 0 > 0 x X x x0 < f(x) f(x0) < .

Положим здесь = f(x0) > 0. Тогда неравенство f(x) f(x0) < f(x0), эквивалентное системе двух неравенств

f(x0) < f(x) f(x0) < f(x0), влечет неравенство

f(x) > 0,

справедливое для всех x из -окрестности точки x0. Теорема 3 доказана.

113

Лекция 12

1. Критерий Коши существования предела функции

2. Односторонние пределы и непрерывность функции

3. Односторонние пределы монотонной функции

4. Классификация точек разрыва функции

5. Символы O и o

1. Критерий Коши существования предела функции

Выведем критерий Коши существования предела функции в точке, аналогичный по смыслу критерию Коши сходимости последовательности.

Теорема 1. Функция f имеет предел в точке x0 на множестве X тогда и только тогда, когда выполняется условие

Доказательство. Утверждение теоремы 1 имеет характер необходимого и достаточного условия существования предела функции. Начнем с доказательства необходимости условия. Предположим, что функция f имеет предел l в точке x0 на множестве X. Тогда по определению Коши

> 0 > 0 x X, x x0, x x0 < f(x) l < .

Помимо точки x, выберем произвольно точку x X, x x0, x x0 < . Согласно определению предела функции для x также, как и для x, выполняется неравенство

f(x ) l < .

114

Осталось записать нехитрую логическую цепочку соотношений, основанную на сложении двух неравенств

> 0 > 0 x X, x X, x x0, x x0, x x0 < и x x0 <

f(x) f(x ) = f(x) l + l f(x ) f(x) l + l f(x ) < + = 2 .

Поскольку - произвольное положительное число, то и 2 - тоже произвольное положительное число, поэтому последнее условие эквивалентно условию Коши в формулировке теоремы 1. Это доказывает необходимость условия Коши для существования предела функции.

Перейдем к доказательству достаточности условия Коши. Пусть выполняется условие теоремы 1. Выберем произвольно на множестве X последовательность точек x1, x2, ..., xn, ..., отличных от x0, сходящуюся к x0. По определению предела последовательности

n0 n > n0 xn x0 < .

Пусть n > n0 и m > n0. Для xn и xm выполнены неравенства

xn x0 < и xm x0 < и следовательно,

f(xn) f(xm) < .

Собирая все условия воедино, запишем логическую цепочку

> 0 n0 n > n0, m > n0 f(xn) f(xm) < ,

115

которая означает фундаментальность последовательности f(x1), f(x2), ..., f(xn), ... . По критерию Коши эта последовательность сходится, limn xn = l.

Осталось показать, что предел l не зависит от выбора последовательности точек. Пусть на множестве X даны две последовательности точек x1, x2, ..., xn, ... иx1 ,x2 , ...,xn , ..., отличных от x0, сходящихся к x0. По доказанному

Образуем последовательность точек

x1,x1 , x2,x2 , ..., xn,xn , ...,

отличных от x0, сходящуюся к x0. По доказанному последовательность

f(x1),f(x1 ), f(x2),f(x2 ), ..., f(xn),f(xn ), ...

также сходится. Поскольку числа l и l являются ее частичными пределами, то l = l . Таким образом, предел l не зависит от выбора последовательности точек. Теперь по определению Гейне заключаем, что функция f имеет предел l в точке x0 на множестве X и завершаем доказательство теоремы 1.

2. Односторонние пределы и непрерывность функции

В определениях Коши и Гейне предела и непрерывности функции выбор точек x или xn был весьма произвольным. Если ограничить свой выбор точками, расположенными по одну сторону от x0, то придем к понятию одностороннего предела и односторонней непрерывности функции в точке. Будем считать, что множество X определения функции f содержит некоторую

полуокрестность {x: x0 < x < x0} в одном случае и {x: x0 < x < x0 + } в другом случае. Начнем с определений Коши.

Определение 1. Число l называется пределом слева функции f в точке x0, если

116

> 0 > 0 x X x0 < x < x0 f(x) l < ,

и обозначается

Если, кроме того, функция f определена в точке x0 и f(x0) = l, то f называется непрерывной слева в точке x0.

Аналогично число l называется пределом справа функции f в точке x0, если

> 0 > 0 x X x0 < x < x0 + f(x) l < ,

и обозначается

Если, кроме того, функция f определена в точке x0 и f(x0) = l, то f называется непрерывной справа в точке x0.

117

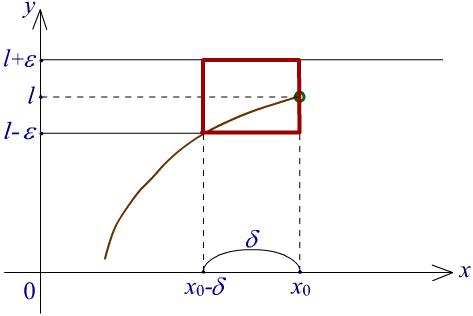
Рис. 1. Иллюстрация к определению непрерывной слева функции.

118

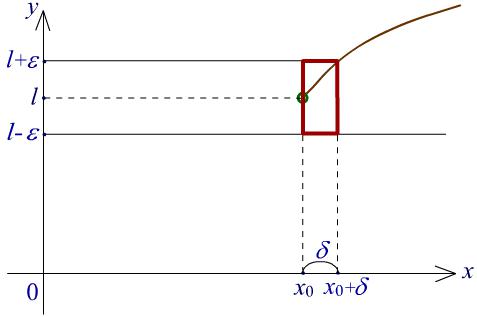
Рис. 2. Иллюстрация к определению непрерывной справа функции.

Подобным образом обобщим определения Гейне.

Определение 2. Число l называется пределом слева функции f в точке x0, если для любой последовательности точек x1, x2, ..., xn, ...

из X таких, что

выполняется условие

lim f xn l.

n

119

Если, кроме того, функция f определена в точке x0 и f(x0) = l, то f называется непрерывной слева в точке x0.

Аналогично число l называется пределом справа функции f в точке x0, если для любой последовательности точек x1, x2, ..., xn, ... из X таких, что

выполняется условие

lim f xn l.

n

Если, кроме того, функция f определена в точке x0 и f(x0) = l, то f называется непрерывной справа в точке x0.

Определение 3. Пределы слева и справа называются односторонними пределами функции в точке. Непрерывность слева или справа называется односторонней непрерывностью функции в точке.

Практически дословное повторение рассуждений предыдущей лекции приводит к заключению об эквивалентности определений Коши и Гейне односторонних пределов и односторонней непрерывности функции в точке.

Покажем, что односторонние подходы к точке естественным образом связаны с произвольным подходом.

Теорема 2. Функция f имеет предел в точке x0 тогда и только тогда, когда f имеет в этой точке предел слева и предел справа, которые равны между собой.

Доказательство. Докажем сначала необходимость условия теоремы 2. Пусть функция f имеет предел l в точке x0. Тогда по определению Коши

> 0 > 0 x X, x x0, x x0 < f(x) l < .

120