Mat_Analiz_Prokhorov

Зафиксируем x1 и устремим x к x0. Тогда отношения (f(x1))/f(x) и (g(x1))/g(x) бесконечно малы и поэтому значение функции

g(x1) 1

g(x) 1 f (x1 ) 1

f (x)

стремится к 0 при x x0. Значит, существует 2 > 0 такое, что для всех x, x0 < x < x0+ 2, справедливо неравенство

g(x1 ) 1 g(x)

(4) f (x1 ) 1 1 . f (x)

Собираем вместе неравенства (1), (2) и (4) и применяем их в неравенстве (3) и, полагая * = min{ , 1, 2}, получим

что выражается условием

Симметричными рассуждениями покажем, что

171

Из двух последних равенств следует, что

что заканчивает доказательство теоремы 5.

Обе теоремы 4 и 5 справедливы и в случае, когда x0 = или x0 = . Доказательства слегка подправляются в соответствии с появившимися изменениями в толковании точки x0 как бесконечно удаленной точки.

Правило Лопиталя позволяет в случае успешного применения заменить поиск предела отношения бесконечно малых или бесконечно больших поиском предела отношения их производных.

172

Лекция 17

1. Критерий монотонности функции

2. Производные высших порядков

3. Формула Тейлора с остатком Пеано

4. Формула Тейлора с остатком Лагранжа

5. Достаточное условие экстремума функции

1. Критерий монотонности функции

Покажем, какие средства предоставляет дифференциальное исчисление для установления монотонности функции на интервале.

Теорема 1. Пусть функция f дифференцируема на интервале (a, b). Функция f не убывает на (a, b) тогда и только тогда, когда f (x) 0 на (a, b). Функция f не возрастает на (a, b) тогда и только тогда, когда f (x) 0 на (a, b).

Доказательство. Проведем доказательство для неубывающей функции f, а для невозрастающей функции рассуждения симметричны.

Начнем с необходимости условия. Пусть функция f не убывает на (a, b). Выберем произвольно точку x0 (a, b) и найдем производную

f '(x0 ) lim f (x) f (x0 ) .

Пусть x > x0. Тогда x x0 > 0 и f(x) f(x0) 0 благодаря тому, что функция f не убывает. Следовательно,

f (x) f (x0 ) 0 x x0

173

и поэтому

Поскольку x0 - произвольная точка из (a, b), то f (x) 0 для всех x (a, b).

Теперь докажем достаточность условия. Пусть f (x) 0 на (a, b). Выберем произвольно точки x1 (a, b) и x2 (a, b), x1 < x2.

Функция f дифференцируема на [x1, x2]. Применим теорему Лагранжа к f на [x1, x2], согласно которой найдется точка c (x1, x2) такая, что

f(x2) f(x1) = f (c)(x2 x1).

Так как f (c) 0 и x2 x1 > 0, то f(x2) f(x1) 0, что означает неубывание функции f на (a, b) и заканчивает доказательство теоремы 1.

2. Производные высших порядков

Дадим индуктивное определение производных второго и произвольного порядков.

Определение 1. Пусть в некоторой -окрестности точки x0 функция f имеет производную f , которая, в свою очередь, является функцией, дифференцируемой в точке x0. Тогда функция f называется дважды дифференцируемой в точке x0 и

(f ) (x0)

называется производной второго порядка функции f в точке x0 и обозначается

f (x0).

Предположим, что в -окрестности точки x0 функция f имеет производную f(k 1), которая, в свою очередь, является функцией, дифференцируемой в точке x0. Тогда функция f называется k раз дифференцируемой в точке x0 и

174

(f(k 1)) (x0)

называется производной порядка k функции f в точке x0 и обозначается

f(k)(x0).

Таким образом, f(k)(x0) = (f(k 1)) (x0).

3. Формула Тейлора с остатком Пеано

Согласно определению дифференцируемой в точке x0 функции f ее можно приблизить линейной функцией с погрешностью

более высокого порядка малости при x x0. Понятие производных высших порядков обобщает это определение, заменив линейную функцию на многочлен степени, равной порядку дифференцируемости. Воплощение такого подхода содержится в следующей теореме.

Теорема 2. Пусть функция f дифференцируема n раз в точке x0. Тогда существует бесконечно малая при x x0 функция такая, что справедлива формула

называется многочленом Тейлора, а погрешность

(x)(x x0)n

приближения функции f многочленом Тейлора называется остатком Пеано. Теорема 2 представляет формулу Тейлора с остатком Пеано.

175

Доказательство. Проведем доказательство по индукции. Для n = 1 утверждение теоремы 2 и формула Тейлора превращаются в определение дифференцируемой в точке x0 функции и поэтому справедливы.

Предположим, что утверждение теоремы 2 и формула Тейлора справедливы для k = 1, 2, ..., n 1 и докажем их для k = n.

Обозначим

Rn(x) = f(x) Tn(x).

Смысл теоремы 2 состоит в том, что Rn(x) = (x)(x x0)n. Будем доказывать это соотношение.

Прежде всего заметим, что всякий многочлен является сколько угодно раз дифференцируемой функцией в любой точке.

Поэтому функция Rn дифференцируема n раз в точке x0. Найдем производную Rn в произвольной точке дифференцируемости

Rn

С другой стороны, коль скоро функция f дифференцируема n раз в точке x0, то ее производная f дифференцируема (n 1) раз в точке x0. Согласно гипотезе индукции для f справедлива формула Тейлора с многочленом Тейлора порядка (n 1). Значит, существует бесконечно малая при x x0 функция такая, что справедлива формула

176

Сравнивая формулы (1) и (2), приходим к выводу, что

(3) Rn (x) = (x)(x x0)n 1.

Обратим внимание, что Rn(x0) = f(x0) Tn(x0) = f(x0) f(x0) = 0. Выберем произвольно точку x из -окрестности точки x0, где Rn дифференцируема, и применим к Rn теорему Лагранжа на отрезке с концевыми точками x и x0, согласно которой между x и x0 найдется точка c такая, что справедлива формула

Rn(x) = Rn(x) Rn(x0) = Rn (c)(x x0).

Эта формула вместе с (3) дает равенство

Rn(x) = (c)(c x0)n 1(x x0).

Очевидно, что

и если x стремится к x0, то и промежуточная точка c стремится к x0. Поэтому

Таким образом, мы доказали, что функция

(x) xRn (xx) n

( 0 )

177

является бесконечно малой при x x0, что заканчивает доказательство теоремы 2.

4. Формула Тейлора с остатком Лагранжа

Если на функцию f наложить условия более жесткие, чем в теореме 2, то и информация о погрешности приближения функции ее многочленом Тейлора будет богаче.

Теорема 3. Пусть функция f дифференцируема (n + 1) раз в -окрестности точки x0. Тогда для всякой точки x из - окрестности точки x0 найдется точка c, находящаяся между x и x0, такая, что справедлива формула

Как и прежде, многочлен Tn в правой части формулы в теореме 3 называется многочленом Тейлора, а погрешность

f n(n 1) (c) (x x0 )n 1

( 1)!

приближения функции f многочленом Тейлора называется остатком Лагранжа. Теорема 3 представляет формулу Тейлора с остатком Лагранжа.

Доказательство. Обозначим

Rn(x) = f(x) Tn(x).

Смысл теоремы 3 состоит в том, что Rn(x) равен остатку Лагранжа. Заметим, что функция Rn дифференцируема (n + 1) раз в-окрестности точки x0, Rn(x0) = 0. Для доказательства выберем произвольно точку x из -окрестности точки x0 и на отрезке с концевыми точками x и x0 применим теорему Коши к паре функций F1 = Rn и G1, где G1(x) = (x x0)n+1. Обе функции

диференцируемы на рассматриваемом отрезке, G1(x0) = 0, G1(x) 0 и G1 (x) 0, если x x0. Согласно теореме Коши между x и x0 найдется точка c1 такая, что справедлива формула

178

Снова на отрезке с концевыми точками c1 и x0 применим теорему Коши к паре функций F2 = F1 и G2 = G1 . Обе функции

дифференцируемы на рассматриваемом отрезке, F2(x0) = f (x0) Tn (x0) = 0, G2(x0) = 0, G2(x) 0 и G2 (x) 0, если x x0. Согласно теореме Коши между c1 и x0 найдется точка c2 такая, что справедлива формула

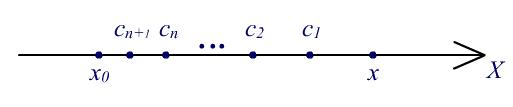
Рис. 1. Иллюстрация к доказательству теоремы о формуле Тейлора с остатком Лагранжа

И так далее. На n-м шаге на отрезке с концевыми точками cn 1 и x0 применим теорему Коши к паре функций Fn = F1(n 1) и Gn = G1(n 1). Обе функции дифференцируемы на рассматриваемом отрезке, Fn(x0) = f(n 1)(x0) Tn(n 1)(x0) = 0, Gn(x0) = 0, Gn(x) 0 и Gn (x) 0, если x x0. Согласно теореме Коши между cn 1 и x0 найдется точка cn такая, что справедлива формула

На последнем шаге на отрезке с концевыми точками cn и x0 применим теорему Лагранжа к функции Fn+1 = F1(n). Эта функция

дифференцируема на рассматриваемом отрезке, Fn+1(x0) = f(n)(x0) Tn(n)(x0) = 0. Согласно теореме Лагранжа между cn и x0 найдется точка cn+1 такая, что справедлива формула

в которой мы учли, что (n + 1)-я производная Tn(n+1)(x) многочлена степени не выше n тождественно обращается в нуль.

Возвращаясь к началу цепочки равенств и начальным обозначениям, убеждаемся, что

179

где c = cn+1, что соответствует сформулированному виду погрешности приближения функции f многочленом Тейлора и заканчивает доказательство теоремы 3.

5. Достаточное условие экстремума функции

Теорема Ферма дает необходимое условие экстремума дифференцируемой функции, которое накладывает требование на значение производной первого порядка. Привлечение к исследованию производных высших поряков дает достаточное условие экстремума.

Теорема 4. Пусть функция f дважды дифференцируема в точке x0 и удовлетворяет условиям:

f (x0) = 0;

f (x0) 0.

Тогда функция f имеет в точке x0 локальный минимум, если f (x0) > 0, или имеет локальный максимум в точке x0, если f (x0) < 0.

Доказательство. Так как функция f дважды дифференцируема в точке x0, то к ней применима формула Тейлора с остатком Пеано, согласно которой существует бесконечно малая при x x0 функция такая, что справедлива формула

Учитывая условие f (x0) = 0 теоремы, запишем оставшуюся часть формулы

180