Mat_Analiz_Prokhorov

Остановимся на смысле двойного предела при a и b , который эквивалентно запишем в виде

Первый интеграл в правой части равенства зависит только от a, а второй интеграл - только от b. Значит, двойной предел распадается на сумму двух независимых друг от друга предельных переходов отдельно по a и по b.

Однако может случиться, что несобственный интеграл Римана на оси расходится, но двойной предел существует, если положить a = b. Дадим этому феномену свое название.

Определение 4. Пусть несобственный интеграл Римана

f (x)dx

расходится, но существует предел

lim b f (x)dx.

b b

Тогда этот предел называется главным значением несобственного интеграла Римана от функции f на оси ( , ) и обозначается

В этом случае говорят, что несобственный интеграл Римана сходится в смысле главного значения.

Пример 2. Пусть f(x) = 1/(1+x2). Одной из первообразных функции f является F(x) = arctg x. Вычислим

271

Таким образом, несобственный интеграл Римана

1 dx

1 x2

сходится и равен .

Рис. 2. Иллюстрация к Примеру 2

2. Несобственные интегралы Римана от неограниченных функций

Сходным образом научимся интегрировать неограниченные функции.

Определение 5. Пусть при фиксированных a и b и любом достаточно малом > 0 функция f интегрируема по Риману на отрезке [a, b ] и существует предел

b

lim f (x)dx.

0 a

Тогда этот предел называется несобственным интегралом Римана от функции f на отрезке [a, b] и обозначается

272

b

f (x)dx.

a

В этом случае говорят, что несобственный интеграл Римана сходится. В случае отсутствия предела несобственный интеграл Римана расходится.

Малость > 0 нужна лишь для того, чтобы выполнялось условие a < b .

В определении 5 не говорится прямо, что функция f не ограничена на отрезке [a, b], но именно в этом состоит основная мотивация перехода к рассмотрению несобственного интеграла. Определение 5 не противоречит пониманию интеграла Римана на отрезке в случае интегрируемости по Риману функции f на [a, b]. Действительно, как было доказано в лекции 25, в этом случае интеграл

F(x) x f (t)dt.

a

с переменным верхним пределом интегрирования непрерывен на [a, b], поэтому значение интеграла Римана

равно значению несобственного интеграла Римана в смысле определения 5. Аналогично определим интеграл для функции f, неограниченной в окрестности точки a.

Определение 6. Пусть при фиксированных a и b и любом достаточно малом > 0 функция f интегрируема по Риману на отрезке [a + , b] и существует предел

Тогда этот предел называется несобственным интегралом Римана от функции f на отрезке [a, b] и обозначается

b

f (x)dx.

a

273

В этом случае говорят, что несобственный интеграл Римана сходится. В случае отсутствия предела несобственный интеграл Римана расходится.

Пример 3. Пусть a = 0, b = 1 и f (x) 1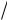x . Одной из первообразных функции f является F(x) 2x . Вычислим

Таким образом, несобственный интеграл Римана

1 1 dx

0 x

сходится и равен 2.

274

Рис. 3. Иллюстрация к Примеру 3

Соединим определения 5 и 6 для рассмотрения несобственного интеграла от функции, неограниченной в окрестности внутренней точки отрезка [a, b].

Определение 7. Пусть при фиксированных a, b и c (a, b) и любых достаточно малых 1 > 0 и 2 > 0 функция f интегрируема по Риману на отрезках [a, c 1] и [c + 2, b] и существует предел

Тогда этот предел называется несобственным интегралом Римана от функции f на отрезке [a, b] и обозначается

b

f (x)dx .

a

В этом случае говорят, что несобственный интеграл Римана сходится. В случае отсутствия предела несобственный интеграл Римана расходится.

275

Рис. 4. Иллюстрация к Определению 7

Однако может случиться, что двойной предел определения 7 не существует, но дело изменится, если положить 1 = 2 = . Как и в случае нефинитных функций, дадим такому пределу название главного значения несобственного интеграла.

Определение 8. Пусть несобственный интеграл Римана

b

f (x)dx

a

расходится, но существует предел

Тогда этот предел называется главным значением несобственного интеграла Римана от функции f на отрезке [a, b] и обозначается

276

v.p.b f (x)dx или p.v.b f (x)dx.

В этом случае говорят, что несобственный интеграл Римана сходится в смысле главного значения.

Исследование всех несобственных интегралов определений 1-8 проводится похожими методами. В дальнейшем мы остановимся на несобственном интеграле определения 1, имея в виду, что все сказанное относится и к остальным типам несобственных интегралов.

3. Линейные операции над несобственными интегралами Римана

Определение 1 cходимости несобственного интеграла Римана

f (x)dx

a

равносильно существованию предела limb F(b) интеграла с переменным верхним пределом интегрирования

F(b) b f (t)dt.

a

Поскольку интеграл Римана и операция предельного перехода в теории функций инвариантны относительно линейных операций над функциями, то та же инвариантность проявляется в теории несобственных интегралов Римана. Выразим эту мысль в следующей теореме.

Теорема 1 Пусть несобственные интегралы Римана

f (x)dx и g(x)dx

aa

сходятся и . Тогда несобственные интегралы Римана

f (x)dx и ( f g )(x)dx

aa

сходятся и справедливы формулы

277

f (x)dx f (x)dx,

aa

( f g)(x)dx f (x)dx g(x)dx.

a a a

Доказательство. Утверждения теоремы 1 о сходимости несобственных интегралов Римана и формулы для интегралов следуют из преобразований

которые заканчивают доказательство теоремы 1.

278

Лекция 28.

1. Критерий Коши сходимости несобственных интегралов Римана 2. Критерий сходимости несобственных интегралов Римана от неотрицательных функций 3. Абсолютная сходимость несобственного интеграла Римана

4. Признак мажорации сходимости несобственных интегралов Римана

5. Признак сравнения сходимости несобственных интегралов Римана

1. Критерий Коши сходимости несобственных интегралов Римана

Определение сходимости несобственного интеграла Римана

f (x)dx

a

равносильно существованию предела limb F(b) интеграла с переменным верхним пределом интегрирования

В лекции 12 был доказан критерий Коши существования предела функции в конечной точке x0. Поскольку понятие предела

функции было перенесено на случай x0 = , то равным образом можно переформулировать критерий Коши существования предела limb F(b) в виде

> 0 b > a b , b b > b и b > b F(b ) F(b ) < .

Не ограничивая общности, будем считать, что b > b . Пользуясь аддитивностью интеграла Римана, преобразуем разность F

(b ) F(b )

279

и переформулируем критерий Коши существования предела limb F(b) как критерий Коши сходимости несобственных интегралов Римана.

Теорема 1 Пусть при фиксированном a и любом b > a функция f интегрируема по Риману на отрезке [a, b]. Несобственный интеграл Римана

Разумеется, теорема 1 не требует нового доказательства

2. Критерий сходимости несобственных интегралов Римана от неотрицательных функций

Рассмотрим несобственный интеграл Римана от неотрицательной функции f 0. По-прежнему пусть функция F задается формулой (1). Воспользовавшись равенством (2) для a < b < b , получим неравенство

F(b")-F(b')= b '' f (x)dx 0,

b'

которое означает, что функция F не убывает на [a, ). Таким образом, условие f 0 влечет монотонность функции F. В лекции 12 было доказано, что всякая монотонная ограниченная функция имеет односторонние пределы в точке x0. С другой стороны, неограниченная функция не может иметь предела в точке. Те же утверждения переносятся на случай бесконечно

удаленной точки x0 = . Таким образом, мы пришли к формулировке следующей теоремы, которая является критерием сходимости несобственных интегралов Римана от неотрицательных функций.

Теорема 2 Пусть при фиксированном a и любом b > a неотрицательная функция f 0 интегрируема по Риману на отрезке [a, b]. Несобственный интеграл Римана

f (x)dx

a

280