Mat_Analiz_Prokhorov

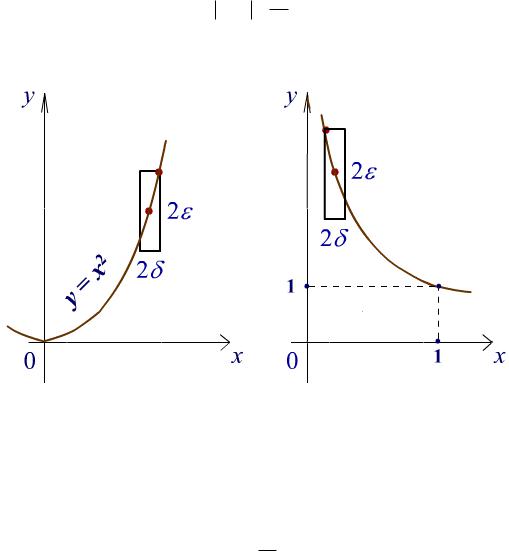
x x' 2 ,

что не может выполняться для достаточно больших x и x . Полученное противоречие показывает, что функция f не является равномерно непрерывной на , хотя, конечно, непрерывна в каждой точке.

Рис. 1. Иллюстрация различия понятий непрерывности и равномерной непрерывности на примере функции y = x2 Пример 2. Пусть f(x) = 1/x, X = (0, 1). Предположим, что f равномерно непрерывна на X. Тогда

Положим, например, в последнем неравенстве x x = /2 и получим xx'> 2 ,

131

что не может выполняться для x, x , достаточно близких к 0. Полученное противоречие показывает, что функция f не является равномерно непрерывной на (0, 1), хотя, конечно, непрерывна в каждой точке.

2. Теорема Кантора

Противоречие примера 1 возникло при неограниченно больших x, x , а в примере 2 противоречие возникло при бесконечно малых

x, x . Подобный выбор точек невозможен в случае, когда X является отрезком. Покажем, что непрерывность функции на отрезке равносильна ее равномерной непрерывности. Следующая теорема принадлежит Кантору.

Теорема 1. Если функция f непрерывна на отрезке [a, b], то f равномерно непрерывна на [a, b].

Доказательство. Проведем доказательство от противного. Предположим, что функция f непрерывна на отрезке [a, b], но не является равномерно непрерывной. Запишем отрицание условия равномерной непрерывности

> 0 > 0 x, x [a, b] x x < и f(x) f(x ) .

Используем возможность произвольного выбора . Положим = 1, тогда

x1,x 1 [a, b] x1 x 1 < 1 и f(x1) f(x 1) . Выберем = 1/2, тогда

Продолжим процесс неограниченно. В итоге получим две последовательности x1, x2, ..., xn, ... иx 1,x 2, ...,x n, ..., удовлетворяющие перечисленным условиям. По теореме Больцано-Вейерштрасса первая из этих двух ограниченных последовательностей содержит сходящуюся подпоследовательность xn1, xn2, ..., xnk, ... . Обозначим

limk xnk x0.

132

Поскольку для всех k 1 справедливы неравенства a xnk b,

то те же неравенства справедливы и для x0, то есть x0 [a, b].

Из равенстваx nk = xnk +(x nk xnk), где первое слагаемое сходится к x0, а второе - к 0, следует, что подпоследовательностьx n1,x n2, ..., xnk ,... второй из полученных последовательностей также сходится к x0.

Образуем последовательность xn1,x n1, xn2,x n2, ..., xnk,x nk, ...,

которая, очевидно, сходится к x0. Напомним, что функция f, непрерывная на отрезке [a, b], непрерывна и в точке x0 [a, b]. Следовательно, по определению Гейне последовательность

f(xn1),f(x n1), f(xn2),f(x n2), ..., f(xnk),f(x nk), ...

сходится к f(x0). По критерию Коши эта последовательность фундаментальна, что противоречит неравенству

f(xnk) f(x nk) ,

справедливому для всех k 1. Противоречие устанавливает ложность сделанного предположения и заканчивает доказательство теоремы 1.

3. Первая теорема Вейерштрасса

Кроме равномерной непрерывности, свойство непрерывности на отрезке гарантирует и другие любопытные глобальные свойства функции. Так, в отличие от примеров 1 и 2, такие функции обязаны быть ограниченными, что будет доказано в следующей теореме, известной под названием первой теоремы Вейерштрасса.

Теорема 2. Если функция f непрерывна на отрезке [a, b], то она ограничена на этом отрезке.

Доказательство. Пусть функция f непрерывна на отрезке [a, b]. Покажем, что она ограничена, то есть

M x [a, b] f(x) M.

133

Проведем доказательство от противного. Предположим, что функция f не ограничена. Запишем отрицание условия ограниченности

M x [a, b] f(x) > M.

Используем возможность произвольного выбора M. Положим M = 1, тогдаx1 [a, b] f(x1) > 1.

Выберем M = 2, тогдаx2 [a, b] f(x2) > 2.

И так далее. На n-м шаге выберем M = n, тогдаxn [a, b] f(xn) > n.

Продолжим процесс неограниченно. В итоге получим последовательность x1, x2, ..., xn, ..., удовлетворяющую перечисленным условиям. По теореме Больцано-Вейерштрасса эта ограниченная последовательность содержит сходящуюся подпоследовательность xn1, xn2, ..., xnk, ... . Обозначим

limk xnk x0.

Поскольку для всех k 1 справедливы неравенства a xnk b,

то те же неравенства справедливы и для x0, то есть x0 [a, b].

Напомним, что функция f, непрерывная на отрезке [a, b], непрерывна и в точке x0 [a, b]. Следовательно, по определению Гейне последовательность

f(xn1), f(xn2), ..., f(xnk), ...

сходится к f(x0) и поэтому ограничена, что противоречит неравенствуf(xnk) > nk,

134

справедливому для всех k 1. Противоречие устанавливает ложность сделанного предположения и заканчивает доказательство теоремы 2.

4. Вторая теорема Вейерштрасса

Еще одно свойство непрерывных на отрезке функций выражено в следующей теореме, которую назовем второй теоремой Вейерштрасса.

Теорема 3. Если функция f непрерывна на отрезке [a, b], то она достигает на этом отрезке своего максимума и минимума.

Доказательство. Обозначим через Y образ отрезка [a, b] при отображении f. По первой теореме Вейерштрасса функция f ограничена, поэтому множество Y ограничено. Пусть

Смысл утверждения теоремы 3 состоит в том, что Y и Y. Оба утверждения доказываются симметрично, поэтому проведем подробное доказательство лишь для .

По свойству верхней грани множества существует последовательность y1, y2, ..., yn, ... точек из множества Y, сходящаяся к .

Каждому yn Y соответствует точка xn [a, b] такая, что yn = f(xn). Как и прежде, ограниченная последовательность x1, x2, ..., xn, ...

содержит сходящуюся подпоследовательность xn1, xn2, ..., xnk,... . Обозначим

limk xnk x0.

Поскольку для всех k 1 справедливы неравенства a xnk b,

то те же неравенства справедливы и для x0, то есть x0 [a, b].

Напомним, что функция f, непрерывная на отрезке [a, b], непрерывна и в точке x0 [a, b]. Следовательно, по определению Гейне последовательность

f(xn1), f(xn2), ..., f(xnk), ...

135

сходится к f(x0). Однако она является подпоследовательностью yn1, yn2, ..., ynk, ... последовательности y1, y2, ..., yn, ..., сходящейся к . Поскольку подпоследовательность сходящейся последовательности сходится к тому же пределу, то

= f(x0).

Мы доказали, что является образом точки x0 [a, b] при отображении f и поэтому Y, что завершает доказательство теоремы 3.

5. Лемма о вложенных отрезках

Мы намереваемся вывести еще одно принципиальное свойство непрерывных на отрезке функций, но прежде подготовим для него вывод о том, что последовательность вложенных отрезков, длины которых стремятся к 0, имеет единственную точку, общую для всех отрезков. Этот факт относится к теории действительных чисел, где играет заметную роль в сравнении различных моделей.

Сформулируем результат в том виде, в котором станем использовать в последующих теоремах.

Лемма. Пусть дана последовательность вложенных отрезков

[a1, b1] [a2, b2] ... [an, bn] ...

такая, что

lim(bn an ) 0.

n

Тогда существует точка c такая, что c = limn an = limn bn.

Рис. 2. Иллюстрация к лемме о вложенных отрезках

Доказательство. Последовательность a1, a2, ..., an, ... левых крайних точек системы вложенных отрезков не убывает, в то время как последовательность b1, b2, ..., bn, ... их правых крайних точек не возрастает. Причем первая последовательность ограничена

136

сверху, поскольку an b1 для всех n 1, а вторая последовательность ограничена снизу, поскольку bn a1 для всех n 1. Следовательно, обе последовательности сходятся. Обозначим

c2 c1 = (c2 bn) + (bn an) + (an c1)

все три слагаемых в правой части являются бесконечно малыми при n . Поэтому, переходя в этом равенстве к пределу при n , получаем равенство

c1 = c2,

доказывающее теорему 4. Очевидно, что для любого n 1

an supn 1 an = c1 = c2 = infn 1 bn bn,

поэтому точка c = c1 = c2 принадлежит всем отрезкам [an, bn], n 1.

137

Лекция 14

1. Теорема Коши о промежуточном значении

2. Непрерывность обратной функции

3. Дифференцируемые функции и производная

4. Непрерывность дифференцируемой функции

1. Теорема Коши о промежуточном значении

Геометрически совершенно ясно, что если функция f непрерывна на отрезке [a, b], в одной концевой точке принимает отрицательное значение, а в другой концевой точке - положительное значение, то график функции пересечет ось OX в некоторой

точке x0 [a, b].

Рис. 1. Непрерывная функция, принимающая в концевых точках значения разного знака

138

Как ни удивительно, доказательство этого факта требует значительных аналитических усилий. Следующая теорема принадлежит Коши.

Теорема 1. Если функция f непрерывна на отрезке [a, b], то она принимает на этом отрезке все промежуточные значения между минимальным и максимальным.

Доказательство. Прежде всего подтвердим, что согласно второй теореме Вейерштрасса непрерывная на отрезке [a, b] функция f достигает своего минимума и максимума. Таким образом, существуют точки a1 [a, b] и b1 [a, b] такие, что

Предположим, например, что a1 < b1, в противном случае проведем симметричные рассуждения.

Выберем произвольно число , промежуточное между m и M, m < < M. Требуется доказать, что найдется точка c [a1, b1], для которой f(c) = . Образуем функцию

Функция g непрерывна на [a, b], g(a1) = m < 0, g(b1) = M > 0. Ясно, что равенство f(c) = равносильно g(c) = 0. Разделим отрезок [a1,b1] пополам точкой (a1 + b1)/2. Если

g( a1 2 b1 ) 0,

то искомая точка c = (a1 + b1)/2 найдена. В противном случае из двух половин [a1, (a1 + b1)/2] и [(a1 + b1)/2, b1] отрезка [a1, b1] выберем ту, на концах которой функция g принимает значения разных знаков. Обозначим выбранную половину через [a2, b2].

139

Рис. 2. Иллюстрация к доказательству теоремы Коши о промежуточном значении Снова разделим отрезок [a2, b2] пополам точкой (a2 + b2)/2. Если

g( a2 b2 ) 0, 2

то искомая точка c = (a2 + b2)/2 найдена. В противном случае из двух половин [a2, (a2+b2)/2] и [(a2 + b2)/2, b2] отрезка [a2, b2] выберем ту, на концах которой функция g принимает значения разных знаков. Обозначим выбранную половину через [a3, b3].

И так далее. На n-м шаге разделим отрезок [an, bn] пополам точкой (an + bn)/2. Если

g( an bn ) 0, 2

то искомая точка c = (an + bn)/2 найдена. В противном случае из двух половин [an, (an + bn)/2] и [(an + bn)/2, bn] отрезка [an, bn] выберем ту, на концах которой функция g принимает значения разных знаков. Обозначим выбранную половину через [an+1, bn+1].

Продолжим процесс неограниченно. В итоге получим последовательность вложенных отрезков [a1, b1] [a2, b2] ... [an, bn] ...,

140