Mat_Analiz_Prokhorov

Следующим действием вновь добавляем положительные члены ряда. Существует минимальное натуральное число n3, для которого

Снова добавляем отрицательные члены ряда. Существует минимальное натуральное число n4, для которого

И так далее. На произвольном нечетном m-м шаге, существует минимальное натуральное число nm, для которого

На следующим за ним шаге существует минимальное натуральное число nm+1, для которого

Процесс продолжим неограниченно.

101

Алгоритм действия составлен так, что каждое неотрицательное слагаемое исходного ряда в некоторый момент будет учтено в

возникает новый ряд, отличающийся от первоначального перестановкой своих членов. На m-м и (m+1)-м шагах справедливы неравенства

По критерию Коши последовательность частных сумм нового ряда расходится, что доказывает второе утверждение теоремы 3. Теорема 3 доказана.

4. Произведение числовых рядов

Мы многократно упоминали ряды е(an + bn), воспринимая их как сумму рядов еan и еbn, и естественно принимали, что частные суммы первого ряда получены сложением частных сумм двух других рядов.

Можно пойти сходным путем в попытке умножения рядов. Именно, если An и Bn - частные суммы рядов еan и еbn, n 1, то

частные суммы Cn ряда-произведения

е cn = е an е bn

должны равняться произведению

102

Есть и другие возможности определения произведения двух рядов. Мы не станем сравнивать различные возможности и доказывать какие-либо теоремы о сходимости (абсолютной или условной) ряда-произведения при условии сходимости рядовсомножителей, ограничившись следующим типичным определением.

Определение 1. Числовой ряд еcn называется произведением числовых рядов еan и еbn, если

5. Понятие о бесконечном произведении

По аналогии с числовым рядом логично определить бесконечное произведение.

Определение 2. Пусть дана последовательность положительных чисел a1, a2, ..., an, ... . Числа

n

P1 a1, P2 a1a2, , Pn a1a2 an Х ak,

k 1

называются частными произведениями. Последовательность P1, P2, ..., Pn, ... называется бесконечным произведением и обозначается an. Если последовательность частных произведений P1, P2, ..., Pn, ... сходится и

lim Pn P > 0,

n

то бесконечное произведение an называется сходящимся, а предел P называется значением бесконечного произведения и обозначается

Хan .

n 1

В противном случае бесконечное произведение называется расходящимся.

103

Мы не станем доказывать специальных теорем о бесконечном произведении, а заметим, что его исследование сводится к исследованию числового ряда еlogan с членами logan и частными суммами

104

Лекция 11

1. Предел и непрерывность функции в точке

2. Эквивалентность определений Коши и Гейне

3. Арифметические действия над непрерывными функциями

4. Непрерывность сложной функции

5. Сохранение знака функции в окрестности точки непрерывности

1. Предел и непрерывность функции в точке

Приступим к изучению поведения функций. Будем обозначать через y = f(x) отображение f: X Y множества X во множество Y. Наиболее интересны случаи, когда множество X являет собой отрезок или интервал числовой оси, включая интервалы с бесконечно удаленными крайними точками.

Одно из основных понятий математического анализа - непрерывность функции в точке, означающее близость значений функции f( x) при близких значениях аргумента x. Начнем с определения чуть более обшего понятия - предела функции в точке, выражающего условие приближения значений f(x) к предельному числу при приближении x к точке x0. Известны два заметно различных подхода к введению понятий предела и непрерывности. Первое из них, высказанное на строгом логическом языке, принадлежит Коши.

Определение 1. Число l называется пределом функции f в точке x0 на множестве X, если

> 0 > 0 x X, x x0, x x0 < f(x) l < ,

и обозначается

105

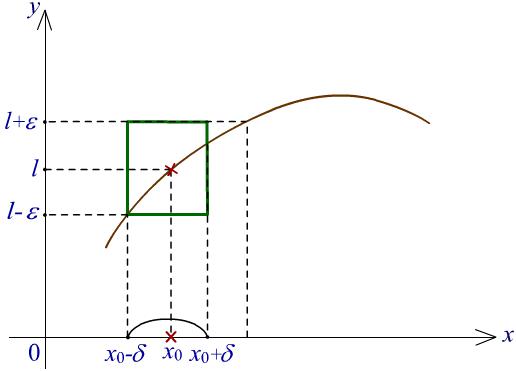
Рис. 1. Иллюстрация к определению предела функции.

Другой подход связан с использованием языка последовательностей и применением накопленных знаний о сходящихся последовательностях. Следующее определение называют именем Гейне.

Определение 2. Число l называется пределом функции f в точке x0 на множестве X, если для любой последовательности x1, x2, ..., xn, ... такой, что xn X, xn x0, n 1, и

lim xn x0 ,

n

выполняется условие

106

lim f xn l.

n

Коль скоро появилось два определения одного и того же понятия, мы должны на этом этапе различать предел в смысле Коши и в смысле Гейне.

Обратим внимание, что в определениях предела функции точка x0 исключается из рассмотрения независимо от того, принадлежит она множеству X или нет. Если все же, во-первых, принять, что x0 X и, во-вторых, f(x0) = l, то в обоих предыдущих определениях

можно снять запрет x x0 или xn x0 и не проверять, что произойдет в таком случае, потому что неравенство в определении Коши тривиально выполняется при x = x0 и требование в определении Гейне нисколько не пострадает, если некоторые из xn окажутся равными x0. Таким образом, естественно приходим к понятию непрерывности функции в точке в смысле Коши и в смысле Гейне.

Определение 3. Пусть x0 X. Функция f называется непрерывной в точке x0 на множестве X, если

> 0 > 0 x X x x0 < f(x) f(x0) < .

В противном случае функция f называется разрывной в точке x0.

Определение 4. Пусть x0 X. Функция f называется непрерывной в точке x0 на множестве X, если для любой последовательности x1, x2, ..., xn, ... такой, что xn X, n 1, и

lim xn x0 ,

n

выполняется условие

lim f xn f x0 .

n

В противном случае функция f называется разрывной в точке x0.

107

Во всех четырех определениях будем опускать слова "на множестве X", если множество X содержит интервал (x0 , x0 + ) с некоторым > 0, за исключением, быть может, самой точки x0 в определениях 1 и 2.

Интервал (x0 , x0 + ) условимся называть -окрестностью точки x0.

Связь между понятиями предела и непрерывности выражается очевидным предложением: функция f непрерывна в точке x0 X,

если limx x0 f x f x0 .

2. Эквивалентность определений Коши и Гейне

Наличие двух смыслов в определениях предела и непрерывности принесло бы много путаницы, однако замечательно, что оба смысла идентичны и мы сможем выбирать любой из подходов в каждой конкретной задаче.

Теорема 1. Определения Коши и Гейне предела или непрерывности функции в точке x0 на множестве X эквивалентны.

Доказательство. Доказательство для предела и непрерывности функции выглядят весьма сходно, поэтому ограничимся, например, демонстрацией эквивалентности понятий непрерывности по Коши и по Гейне.

Начнем с доказательства того, что непрерывность в смысле Коши влечет непрерывность в смысле Гейне. Пусть для функции f выполнены условия определения 3

> 0 > 0 x X x x0 < f(x) f(x0) < .

Выберем произвольно последовательность точек x1, x2, ..., xn, ..., принадлежащих множеству X, такую, что limn xn = x0. По определению предела последовательности

n0 n > n0 xn x0 < .

Тогда по определению 3 выполняется неравенство

108

f(xn) f(x0) < .

Собирая вместе все условия, сформулируем заключение

> 0 n0 n > n0 f(xn) f(x0) < ,

которое означает, что выполняется определение Гейне, так как

lim f xn f x0 .

n

Обратно, покажем теперь, что непрерывность в смысле Гейне влечет непрерывность в смысле Коши. Пусть для функцииf выполнены условия определения 4. Проведем доказательство от противного. Предположим, что функция f не удовлетворяет условию определения 3. Нетрудно записать отрицание предиката. Для этого следует заменить кванторы на противоположные и написать отрицание имеющегося высказывания. Таким образом, отрицание требования в определении 3 представим в виде

И так далее. На n-м шаге если = 1/n, то

109

Продолжим процесс неограниченно. В итоге получим последовательность точек x1, x2, ..., xn, ..., принадлежащих X и удовлетворяющих перечисленным условиям. Так как xn x0 < 1/n, то limn xn = x0. И по определению 4 limn f(xn) = f(x0), что

противоречит неравенству f(xn) f(x0) . Возникшее противоречие доказывает ложность предположения. Следовательно, функция f непрерывна в точке x0 на множестве X в смысле Коши. Теорема 1 доказана.

3. Арифметические действия над непрерывными функциями

Покажем, что понятие непрерывности инвариантно относительно арифметических действий.

Теорема 2. Пусть функции f и g непрерывны в точке x0. Тогда функции f + g, f g, fg и f/g непрерывны в точке x0. В случае частного предполагаем дополнительно, что g(x) 0.

Доказательство. Воспользуемся определением непрерывности по Гейне и инвариантностью понятия предела последовательности относительно арифметических действий. Выберем произвольно последовательность точек x1, x2, ..., xn, ... из области определения функций f и g такую, что limn xn = x0. Тогда по определению Гейне

110