30

распространяющейся от нагрузки к генератору) волн, фазовом сдвиге и затухании в том или ином отрезке линии передачи или в элементах СВЧ тракта достаточно для решения задач такого класса. Во многих случаях падающая волна ассоциируется с прямой волной, а отраженная волна – с обратной. Соответствующую информацию можно получить на основе построения модели какого-либо типа линии передачи в виде эквивалентной длинной линии. Для такой линии вводят эквивалентные нормированные напряжения прямой и обратной волн согласно выражениям

Согласно выражениям (4.7) модули нормированных напряжений прямой и обратной волн являются, по сути, квадратными корнями соответствующих

мощностей и поэтому имеют размерность корень квадратный из Ватт ( Вт ). Фазы нормированных напряжений прямой ϕпр и обратной ϕобр волн считают

равными фазам поперечных компонент электрического поля для соответствующих волн в определённом сечении.

2.3. Коэффициент отражения

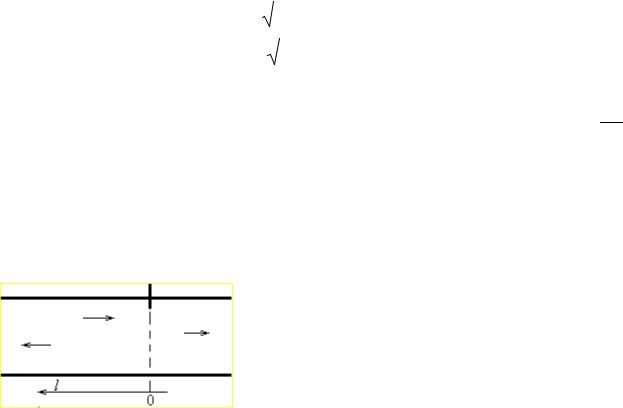
Рассмотрим линию передачи с неоднородностью, в которой распространяется падающая (прямая) волна (рис.2.2). В области неоднородности возникают токи, порождающие волны разных типов. Допустим, линия передачи работает в одноволновом (одномодовом) режиме. Тогда можно считать, что на достаточно большом расстоянии от неоднородности существуют только три волны: падающая

(прямая), отражённая (обратная) и прошедшая за неоднородность.

Если считать, что падающая волна распространяется в направлении положительных значений z, а расстояние l до неоднородности отсчитывать соответственно в отрицательном направлении значений z , причём начало координат l = 0 разместить в сечении, где расположена неоднородность, то для l > 0 полное нормированное напряжение в линии передачи в точке с координатой l будет равняться

и отражённой (обратной) волн в сечении, где расположена неоднородность, то есть для l = 0.

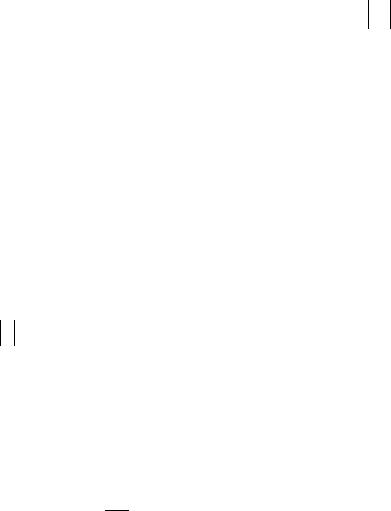
32

передачи конец вектора Γ(l) описывает спираль (рис.2.3). Вращение по часовой

стрелке соответствует перемещению к генератору, а против – к нагрузке. Поворот на 360° соответствует перемещению на расстояние ∆l :

откуда ∆l = Λ / 2 .

При движении в направлении к генератору Γ уменьшается, так как амплитуда uпр (l) увеличивается, а uобр (l) – уменьшается. Период изменения фазы

равен половине длины волны.

В линии передачи без потерь (α=0) вектор Γ(l) описывает окружность.

Для пассивной линии (которая не увеличивает энергию волны) все возможные значения Γ лежат внутри окружности единичного радиуса.

При одновременном существовании падающей и отражённой волн мощность, которая переносится в определённом сечении, определяется выражением (2.15), тогда с учётом введенных нормированных напряжений и коэффициента отражения можно записать

В выражении (2.23) присутствует коэффициент отражения по мощности ΓP = Γ2 . Активную мощность можно представить в несколько ином виде:

где символом * обозначены комплексно сопряженные величины.

Такое представление справедливо, поскольку выражение (Γ − Γ*) является мнимым. Всё это позволяет формально ввести полное нормированное

напряжение u ( Вт ) в виде суммы нормированных напряжений падающей и отражённой волн:

Тогда эквивалентный нормированный ток целесообразно выразить в виде

Нормированный ток падающей волны совпадает с нормированным напряжением, а нормированный ток отраженной волны совпадает по модулю с нормированным напряжением отраженной волны, но имеет противоположный знак.

Согласно выражению (2.25) нормированное напряжение в линии передачи пропорционально напряженности полного поперечного электрического поля

33

в линии в случае суперпозиции падающей и отражённой волн. Как было указано, коэффициент отражения по нормированному напряжению Γ совпадает с коэффициентом отражения по электрическому полю ΓE . Коэффициент отраже-

ния по магнитному полю ΓH имеет противоположный знак по сравнению с коэффициентом отражения по электрическому полю ΓE . Если бы такое соотношение не выполнялось, то, исходя из совпадения знаков векторов Пойнтинга, которое имеет место быть при совпадении знаков ΓE и ΓH , направления рас-

пространения для падающей и отражённой волн совпадали бы вместо того, чтобы быть противоположными. Точно так же в длинной линии коэффициенты отражения по току и напряжению имеют противоположные знаки. Таким образом, полный нормированный ток (2.26) может быть представлен в виде

i = uпад (1+ ΓH ) . Он пропорционален полному магнитному полю. Данное обстоятельство и позволяет рассматривать эту величину как ток.

2.4. Нормированные сопротивление и проводимость

Отношение полного нормированного напряжения u в эквивалентной

длинной линии к полному нормированному току i определяет полное нормиро-

ванное (безразмерное) сопротивление:

Обратная величина определяет полную нормированную (безразмерную)

проводимость:

С помощью нормированных сопротивления и проводимости мощность, распространяющаяся по линии передачи, может быть представлена еще с помощью формул, характерных для теории низкочастотных электрических цепей:

Из формулы (2.27) следует, что при условии Γ = 0, то есть для случая, когда отраженной волны не существует, и в линии устанавливается режим чисто бегущей волны (англ. – travelling wave), отношение нормированных напряжения и тока равно единице. Это означает, что в эквивалентной длинной линии принято единичное безразмерное волновое сопротивление.

В общем случае в линии передачи СВЧ невозможно определить точки, между которыми существует напряжение, или выделить проводники, вдоль которых течет ток, поэтому понятия нормированных напряжения и тока имеют целиком условный характер. Но для линий передачи, в которых распространяется ТЕМ-волна, можно получить связь между нормированными напряжением,

34

током, сопротивлением и действительно существующими напряжением, током

иволновым сопротивлением.

Спомощью описанных ненормированных величин процессы в длинной линии с ТЕМ-волной могут быть описаны известными соотношениями для

Необходимо отметить, что в приведенных формулах коэффициент отра-

жения Γ имеет такой же вид, как в соотношениях (2.25), (2.26).

Сопоставляя формулы (2.30), (2.31) с формулой (2.23), получим соотношения для нормированных напряжения и тока в линии передачи с ТЕМ-волной:

где zн і Zн – соответственно нормированное и ненормированное сопротивления

нагрузки.

Последнее выражение позволяет установить связь коэффициента отражения нагрузки с сопротивлением нагрузки:

Из этого выражения следует, что в случае совпадения сопротивления нагрузки и волнового сопротивления линии коэффициент отражения равен нулю. Такой вывод справедлив для линий с ТЕМ-волной. Что касается полых волноводов, то