25

2.Теория длинных линий

2.1.Основы теории длинных линий

Полный анализ любых электромагнитных систем сводится к расчёту векторов электромагнитного поля, например E и H , в каждой точке пространства в каждый момент времени. Однако довести до конца решение системы уравнений Максвелла удаётся лишь для систем с достаточно простой геометрической конфигурацией.

В ряде случаев все необходимые для практики сведения о свойствах электромагнитных систем и устройств заключаются в оценках уровня мощности, которая передаётся между отдельными точками системы. Такую информацию можно получить, не используя методы электродинамики.

Если в составе системы можно выделить такие области пространства, в которых сконцентрирован преимущественно один из видов энергии, то в случае приближенного рассмотрения выделяют класс квазистационарных электрических цепей. Например, конденсатор концентрирует энергию электрического поля, а катушка индуктивности – магнитного, в резисторе осуществляется процесс преобразования электромагнитной энергии в тепловую, в источниках (генераторах) энергия неэлектромагнитного происхождения трансформируется в энергию электромагнитного поля.

Электромагнитные системы, для которых невозможно применить условия квазистационарности, называют волновыми или системами с распределёнными параметрами (англ. – distributed parameter).

Исторически первым объектом изучения стала линия передачи, образованная двумя параллельными проводниками, при условии, что длина линии либо больше, либо сопоставима с длиной волны. Такие линии передачи назвали

длинными (англ. – long line).

Отрезок линии передачи будем рассматривать как квазистационарный четырёхполюсник. Его внутреннюю структуру выбираем такой, чтобы можно было учитывать:

−накопление энергии электрического и магнитного полей;

−преобразование части энергии в тепло, вызванное сопротивлением проводников и проводимостью изоляции.

Вслучае такого подхода количественными характеристиками линии передачи явля-

ются: погонная индуктивность L1 (Гн/м), по-

26

ной линии передачи, используя комплексные амплитуды напряжения U (z) и тока I(z) от продольной координаты. Будем считать, что зависимость от времени имеет вид exp( jωt). Представим линию как последовательное соединение отрезков длиной ∆ z каждый, при условии ∆ z → 0 такие четырёхполюсники могут быть описаны методами теории электрических цепей. Исходя из данных

Разностные уравнения (2.1) и (2.2) преобразуем в следующую систему уравнений:

Осуществим теперь операцию предельного перехода ∆ z → 0 , в результа-

те чего уравнения (2.3) преобразуются в систему двух обычных дифференциальных уравнений с постоянными коэффициентами:

Эта система дифференциальных уравнений получила название телеграф-

ных уравнений.

Из (2.4) можно легко получить уравнение Гельмгольца относительно U

или I , если обе части одного из уравнений продифференцировать по z, а потом второе уравнение подставить в полученное выражение. Тогда имеем

Общее решение этого уравнение имеет вид

27

где U +,U − – комплексные амплитуды прямой (англ. – direct) и обратной (англ.

– return) волн, которые распространяются в направлении увеличения и уменьшения координаты z , соответственно; γ– постоянная распространения, которая

равняется γ = Z1Y1 .

Каждое из слагаемых описывает чисто бегущую волну. В определенных ситуациях с прямой волной ассоциируется падающая (англ. – incident) волна (волна, которая распространяется от генератора), а с обратной – отраженная (англ. – reflected) волна, обусловленная отражением от нагрузки (англ. – load).

Из первого уравнения в системе (2.4) и явного вида выражения для напряжения (2.6) следует выражение для тока:

Согласно выражению (2.7) ток для обратной волны в отличие от тока прямой волны имеет знак минус. Таким образом, ток в обратной волне направлен в противоположном направлении, при этом считается, что напряжения для прямой и обратной волн направлены одинаково.

Величину W = UI ++ = Zγ1 (Ом), которая определяется отношением ком-

плексных амплитуд напряжения и тока в бегущей волне, называют волновым сопротивлением линии передачи. Для обратной волны выражение, которое

описывает волновое сопротивление, должно иметь вид W = −UI −− . Необходи-

мость знака «минус» обусловлена тем, что токи прямой и обратной волн направлены в противоположные стороны. Тогда уравнение (2.7) приобретает вид

В линии передачи распространяется затухающая волна, скорость изменения амплитуды которой определяется действительной, а фазы – мнимою частью постоянной распространения.

Переходя от комплексной амплитуды к мгновенному значению напряжения, для прямой и обратной волн имеем

Здесь ωt −βz и ωt +βz – полные фазы для прямой и обратной волн, соответственно. Условие ωt −βz = const определяет положение фазового фронта для

28

прямой волны. Фазовая скорость, характеризующая скорость распространения фазового фронта, равна:

Соответственно для обратной волны vф = −ωβ, то есть фазовые скорости

прямой и обратной волн одинаковы по модулю, но направлены в противоположные стороны.

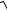
В случае отсутствия потерь α = 0 , β = ωL1C1 , vф =1L1C1 (vф – не зависит от частоты), W = L1C1 .

2.2. Нормированные значения напряжения

Полученные выражения для волн напряжения и тока позволяют определить потоки мощности, которые переносят бегущие волны. Зафиксируем некоторую точку в регулярной линии передачи z = z0 , будем считать, что комплекс-

ные амплитуды напряжения и тока для бегущей волны известны и равны соответственно U (z0 ) и I(z0 ). Это позволяет определить полную среднюю мощность S согласно выражению

Ясно, что в в ыражении (4.1) использованы амплитудные значения напряжения и тока. Если перейти к комплексным действующим (англ. – effective)

В общем случае полная мощность S = P + jQ является комплексной ве-

личиной. Её действительную часть P называют активной мощностью, а мнимую часть Q – реактивной мощностью гармонического электромагнитного

процесса.

Пусть вдоль линии распространяется прямая волна в сторону возрастания координаты z . При этом

Uпр (z) = Iпр (z)W ,

таким образом,

29

(в правой части находится квадрат модуля комплексной амплитуды тока). Если рассматривать обратную волну, для которой

Uобр(z) = −Iобр(z)W ,

то

Для пассивных элементов, то есть для линий передачи, всегда выполняется Re(W ) > 0 , поэтому активная мощность, соответствующая прямой волне,

всегда положительна, а активная мощность обратной волны отрицательна. Разница в знаках мощности связана с противоположностью направлений токов прямой и обратной волн. Таким образом, в регулярной линии передачи направления потоков энергии и фазовые скорости совпадают.

Для мощности, которая переносится в линии, имеем следующее выраже-

ние:

Для трактов, в которых можно пренебречь потерями, в выражениях (2.13)

– (2.16) вместо Re(W ) можно просто использовать W , поскольку для данного

случая волновое сопротивление – величина действительная.

В волноводных трактах СВЧ невозможно ввести традиционные напряжение и ток, такие величины имеют физический смысл только в линиях передачи, в которых распространяются ТEM-волны. Во многих задачах проектирования СВЧ схем информация о структуре поля не является необходимой. Данных об уровне передаваемой мощности или соотношении между мощностями падающей (т.е. распространяющейся от генератора к нагрузке) и отражённой (т.е.