
- •Введение
- •Список сокращений
- •1. Линии передачи СВЧ
- •1.1. Основные положения
- •1.2. Коаксиальная линия передачи.
- •1.3. Двухпроводная линия передачи
- •1.4. «Витая пара»
- •1.5. Прямоугольный волновод
- •1.6. Круглый волновод
- •1.7. Планарные линии передачи
- •2. Теория длинных линий
- •2.1. Основы теории длинных линий
- •2.2. Нормированные значения напряжения
- •2.3. Коэффициент отражения
- •2.4. Нормированные сопротивление и проводимость
- •2.5. Интерференция падающей и отраженной волн в нагруженной линии
- •2.6. Входное сопротивление линии передачи с нагрузкой
- •2.7. Основные режимы работы линии передачи
- •2.8. Круговая диаграмма сопротивлений
- •2.9. Полуволновые и четвертьволновые трансформаторы
- •3. Согласование линий передачи
- •3.1. Общие положения теории согласования линий передачи с нагрузкой
- •3.2. Согласование с помощью четвертьволнового трансформатора
- •3.3. Согласование с помощью сосредоточенной реактивности
- •3.5. Согласование с помощью параллельного реактивного шлейфа.
- •3.6. Трансформаторы с тремя реактивными элементами.
- •4. Матричные методы описания устройств СВЧ
- •4.1. Матрицы рассеяния многополюсников
- •4.2. Волновые матрицы передачи многополюсников
- •5. Двухполюсники
- •5.1. Согласованные нагрузки
- •5.2. Реактивные нагрузки
- •5.3. Преобразователи СВЧ мощности
- •6. Четырехполюсники
- •6.1. Разъемы и соединения
- •6.2. Переходы между линиями разных типов
- •6.3. Нерегулярности в волноводе
- •6.4. Изгибы и скрутки волноводов
- •6.5. Аттенюаторы
- •6.6. Фазовращатели
- •6.7. Согласующие трансформаторы
- •7. Резонаторы и фильтры СВЧ
- •7.1. Объемные резонаторы
- •7.2. Основные типы резонаторов
- •7.3. Открытые резонаторы
- •7.4. Диэлектрические резонаторы
- •7.5. Резонатор, включенный на проход
- •7.6. Частотные фильтры
- •8. Шестиполюсники
- •8.1. Y-тройники
- •8.3. Шестиполюсные делители мощности
- •9. Восьмиполюсники и двенадцатиполюсники
- •9.1. Направленные ответвители
- •9.2. Мостовые устройства
- •9.3. Крестообразные соединения
- •9.4. Резонатор бегущей волны
- •9.5. Двенадцатиполюсники
- •10. Ферритовые устройства СВЧ
- •10.1. Основные свойства ферритов на СВЧ
- •10.2. Ферритовые устройства на эффекте Фарадея
- •10.3. Вентили с поперечно подмагниченным ферритом
- •10.4. Фазовые циркуляторы
- •11. Физические основы работы полупроводниковых приборов СВЧ диапазона
- •11.1. Энергетические зоны полупроводников
- •11.2. Процессы переноса заряда в полупроводниках
- •11.3 Полупроводники в сильных электрических полях
- •11.4. Контактные явления
- •12.1. Полупроводниковые аналоги вакуумных приборов СВЧ
- •12.2 Динамическая отрицательная проводимость
- •12.3. Лавинное умножение носителей заряда
- •12.4 Основные режимы работы ЛПД
- •12.5. Технический уровень промышленно выпускаемых ЛПД
- •13. Полупроводниковые приборы с объемной неустойчивостью (диоды Ганна)
- •13.1. Механизм междолинного перехода
- •13.2 Эффект Ганна и критерий Кремера
- •13.3 Динамика ганновских доменов
- •13.4. Классификация режимов работы генераторов Ганна
- •13.5. Предельные параметры генераторов Ганна
- •13.6. Способы повышения эффективности и верхнего частотного предела генераторов Ганна
- •14.1. Основы полупроводниковой технологии
- •14.2. Конструкции диодных СВЧ генераторов
- •14.3. Способы перестройки частоты
- •15. Повышение мощности полупроводниковых генераторов и освоение миллиметрового диапазона волн
- •15.1. Основные принципы построения СВЧ-сумматоров
- •15.2. Конструкции сумматоров мощности
- •15.3. Освоение миллиметрового и субмиллиметрового диапазонов
- •16. Усилители СВЧ
- •16.1. Основные параметры усилителей
- •16.2. Классификация усилителей СВЧ
- •16.3. Однокаскадный транзисторный усилитель
- •16.4. Принцип действия балансного усилителя
- •17. Преобразователи частоты
- •17.1. Смесители
- •17.2. Преобразование частот в смесителе
- •17.3. Основные параметры смесителей
- •17.4. Небалансные смесители
- •17.5. Балансные смесители
- •17.6. Двойные балансные смесители
- •17.7. Кольцевые балансные смесители
- •17.8. Транзисторные смесители
- •Тесты для самопроверки
- •Ответы на тесты
- •Библиографические ссылки
- •Список рекомендованной литературы
- •Предметный указатель
171
10.Ферритовые устройства СВЧ
10.1.Основные свойства ферритов на СВЧ
Феррит (англ. – ferrite) – магнитодиэлектрический материал с кристаллической структурой, которому присущи гиромагнитные свойства. Относительная диэлектрическая проницаемость ферритов ε находится в пределах 8 – 16, тан-
генс угла электрических потерь tg δ =10−3 −10−2 , магнитная проницаемость при
отсутствии подмагничивания близка к единице. При отсутствии внешнего магнитного поля ферриты на всех частотах являются изотропными м атериалами с взаимными свойствами.
Различают три разновидности кристаллической структуры ферритов: шпинели, граната и гексагональная. Ферриты могут быть поликристаллическими и монокристаллическими. Производство поликристаллических ферритов осуществляется за технологией характерной для керамики – из смеси окислов с пластификатором формируют полуфабрикаты, которые потом спекают при температуре 1000 – 1400°С.
Рассмотрим основные явления в подмагниченных ферритах, на которых основывается работа устройств СВЧ.
ЕВ  ЕВ
ЕВ
|
В |
|
В |
|
ЕА |
L |
|
ЕА |
|
А |
Н0 |
А |
Н0 |
|
a |
б |
|||
|
|
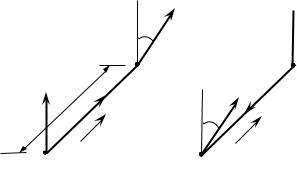
Рис.10.1. Распространение волн в гиротропной среде:
а– по направлению поля подмагничивания,
б– в противоположном направлении
Эффект Фарадея состоит в повороте плоскости поляризации электромагнитной волны при ее распространении вдоль поля подмагничивания H0 . При распространении электромагнитной волны в гиротропной среде из точки А в точку В (рис.10.1,а) по направлению вектора H0 электрический вектор E поворачивается по часовой стрелке на угол ∆ . При обратном распространении
(рис.10.1,б) вектор E поворачивается протии часовой стрелки на тот же угол по ходу волны.
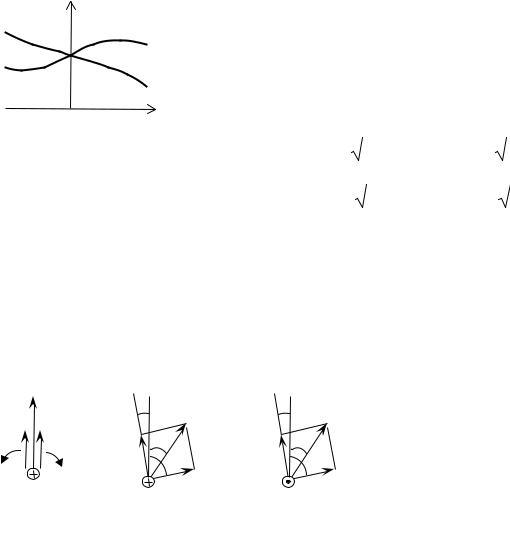
Эффект Фарадея в гиротропных средах объясняется тем, что эффективные магнитные проницаемости для волн круговой поляризации имеют разные значения с правой (µ+ ) и левой поляризации (µ− ). Характер зависимостей µ+ и
µ− для слабого магнитного поля H0 приведен на рис.10.2.
|
|
172 |
|
µ |
|
Линейную поляризацию можно представить |
|
µ− |
|
как суперпозицию двух полей круговой поляриза- |
|
|
ции E + и E − |
(рис.10.3,а), тогда для их фазовых |
|
µ |
+ |
скоростей (v+ , |
v− ) и соответствующих длин волн |
|
ф |
ф |
|
этих полей ( Λ+ , Λ− ) можно записать следующие
|
0 |
|
H0 |
|
выражения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
v+ = с/ |
|
|
|
; |
v− = с/ |
|
|
|
|
; |
(10.1) |
|||||||||||||
Рис.10.2. Эффективные |
|
|
|
|
εµ |
+ |
|
εµ |
− |
|||||||||||||||||||||
магнитные проницаемости |
|
|
|
Ф |
|
|
|
|
|
|
Ф |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
феррита для слабого |
|
|
|
|
Λ+ = λ/ |
|
|
; |
Λ− = λ/ |
|
|
|
. |
(10.2) |
||||||||||||||||
|
|
|
εµ+ |
|
εµ− |
|||||||||||||||||||||||||
|
магнитного поля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
Векторы E + |
и E − |
в точке B (рис.10.3,б) бу- |
|||||||||||||||||||
дут отставать по фазе от соответствующих векторов в точке A за счет разности |
||||||||||||||||||||||||||||||
хода на углы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
ϕ+ = 2πL / Λ+ ; |
|
ϕ− = 2πL / Λ− . |
|
|
|
|
|
|
|
(10.3) |
||||||||||||
Поскольку при прямом распространении ( H0 |
> 0 ) |
µ+ < µ− |
(рис.10.2), вектор |
|||||||||||||||||||||||||||
|
Е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E + |
в |
точке |
B |
отстает |
на |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
меньший угол, |
чем E − . А р е- |
||||||||||||||
|
|
ϕ+ |
|
|
|
ЕB |
ϕ− |
ЕА |
|
|||||||||||||||||||||
Е– |
Е+ |
Е+ |
|
|
|
|
|
Е– |
|
|
|
зультирующий вектор EB |
по- |
|||||||||||||||||
|
|
|
− |
|
|
|
|
ворачивается |
|
|
|
на |
угол |
|||||||||||||||||
|
|
|
|
|
ϕ |
|
|
|
ϕ+ |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
Е– |
|
|
|
|
Е+ |
|
∆ = 0,5(ϕ− − ϕ+ ). |
|
|
|
|
|
||||||||||||
|
А |
|
|
|
B |
|
|
|
А |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При |
обратном |
распро- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
a |
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
странении |
( H0 < 0 ) |
µ+ > µ− |
||||||||||||||
Рис.10.3. Направления |
векторов электрического |
|
|
(рис.10.2) вектор E + |
в точке A |
|||||||||||||||||||||||||
|
поля: а – в начальной точке А, б – в конечной |
|
(рис.10.3,в) |
отстает |
на боль- |
|||||||||||||||||||||||||
|
|
точке В, в – в конечной точке А |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
ший угол, |
чем |
|
|
E − . Результи- |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
рующий вектор EA поворачивается на угол ∆ = 0,5(ϕ+ − ϕ− ). |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
При |
слабых |
полях |
угол |
поворота |
∆ пропорционален |
напряженности |
|||||||||||||||||||||||
подмагничивания |
H0 и расстоянию между точками L . |
При увеличении |
H0 |
|||||||||||||||||||||||||||
наступает насыщение. Эффект Фарадея является невзаимным, то есть угол поворота плоскости поляризации не зависит от направления распространения волны и именно этим объясняется невзаимность эффекта Фарадея. Происхождение термина «гиротропия» связано именно с этим эффектом.
В ферритах в относительно сильном продольном или поперечном магнитном поле наблюдается явление ферромагнитного резонанса. При продольном подмагничивании резонанс имеет место тогда, когда частота волны круговой поляризации правого вращения приближается к частоте прецессии электронов
fII = f0 2,84H0 , |
(10.4) |
|
173 |
|
|
|
где |
f – частота в мегагерцах, а H0 в эрстедах. |
|
||
|
Поперечное подмагничивание дает несколько большую резонансную ча- |
|||
стоту |
|
|||
|
f f0 |
|
, |
|
|
1+ M0 / H0 |
(10.5) |
||
где M 0 – намагниченность феррита. |
|
|||
|
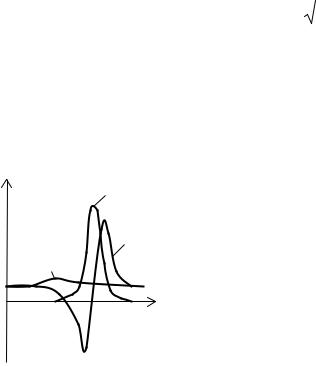
На рис.10.4 показан характер зависимостей магнитных проницаемостей |
|||
феррита для правополяризованной волны µ+ = µ′+ + jµ′+′ |
и левополяризованной |
|||
µ− |
от величины H0 . Из графиков видно, что магнитная проницаемость для |
|||
правополяризованной волны имеет резонансный характер, и мнимая составляющая магнитной проницаемости µ′+′, учитывающая
µ+ , µ− |
µ′+′ |
потери в феррите, максимальна при резонансе. Ре- |
||
|
µ′+ |
зонансный характер магнитной проницаемости µ+ |
||
µ− |
обусловлен тем, что частота и направление воз- |
|||
|
буждающего поля совпадает с частотой и направ- |
|||
0 |
|
лением прецессии электронов. Для левополяризо- |
||
H0 |
ванной волны направление вращения поля и пре- |
|||
|
цессии электронов противоположны, резонанс не- |
|||
|
|
|||
|
|
возможен, и магнитная проницаемость µ− изменя- |
||
Рис.10.4. Компоненты |
ется плавно. |
|
|
|
магнитных проницаемо- |
Частоту резонанса f0 |
путем |
изменения |
|
стей феррита в сильном |
напряженности поля подмагничивания H0 можно |
|||
магнитном поле |
||||
|
|
подобрать равной рабочей |
частоте |
колебаний. |
Правополяризованные волны при распространении в направлении H0 испытывают затухание, а волны, распространяющиеся против вектора H0 , практически
не испытывают затухания.
В тонких ферритовых пластинах в прямоугольном волноводе с волной типа Н10 при поперечном подмагничивании наблюдается невзаимный фазовый сдвиг. Ферритовая пластина располагается между срединой волновода и одной из узких стенок, пластина подмагничивается слабым полем H0 перпендику-
лярно. При этом структура поля волны Н10 почти не нарушается.
Невзаимный фазовый сдвиг обусловлен следующим. Компоненты магнитного поля основной волны в прямоугольном волноводе Н10 определяются следующим образом:
H x = ±A± πsin πx exp[j(ωt βz + ϕ± )]; |
|
|
(10.6) |
||||||
|
a |
|
a |
|
|
|
|
|
|
H z = − jA |
± |
π 2 |
1 |
cos |
πx |
exp[j(ωt βz + ϕ |
± |
)], |
(10.7) |
|
|
γ |
a |
|
|||||
|
a |
|
|
|
|
|
|||
174
где A – амплитуда волны; β – постоянная распространения; ϕ – начальная фа-
за; верхний и нижний индексы относятся соответственно к волнам, которые распространяются в направлении увеличения и уменьшения координаты z .
Если амплитуду составляющей H Z принять равной единице, тогда
H x = ± j |
2a |
sin |
πx exp[j(ωt βz + ϕ± )]; |
(10.8) |
|
||||
|
Λ |
a |
|
|
H z = cos |
πx exp[j(ωt βz + ϕ± )], |
(10.9) |
||
|
a |
|
|
|
где Λ – длина волны в волноводе.
|
|
|
Н0 |
y |
Распространение |
|
Наличие |
множителя |
± j |
в |
|||||
|
|
|
уравнении |
(10.8) указывает |
на |
то, |
|||||||||
|
|
|
|
|
волны |
что компоненты поля H z |
и |
H x |
|||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
z |
сдвинуты |
по |
фазе |
относительно |
||||||
|
|
|
|
|
друг друга соответственно на ±90°. |
||||||||||
|
|
|
|
|
|
||||||||||
b |
|
|
|
|
Таким образом, существуют две |
||||||||||
|
|
|
|
симметричные |
плоскости x1 |
и |
x2 |
||||||||
x |
x2 |
a |
x1 |
|
0 |
(рис.10.5), |
в |
которых |
амплитуды |
||||||
|
|
|
|
|
компонент одинаковы |
|
H z = H x |
и |
|||||||
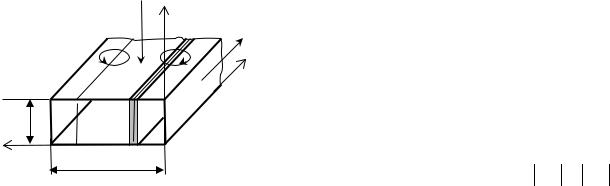
Рис.10.5. Положения плоскостей круго- |
|
||||||||||||||
поле |
H имеет круговую поляриза- |
||||||||||||||
|
вой поляризации в прямоугольном |
||||||||||||||
|
цию. |
Положения этих |
плоскостей |
||||||||||||
|
|
|
волноводе |
||||||||||||
амплитуды компонент (10.8) и (10.9): |
можно |
определить, |
|
приравнивая |
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||
2a |
sin |
πx |
= cos |
πx |
(10.10) |
|
a |
a |
|||
Λ |
|
|
|||
и находя корни этого уравнения
x |
= a arctg |
Λ |
; |
x |
|
= a − x . |
(10.11) |
2a |
|
||||||
1 |
π |
|
|
2 |
1 |
|
В плоскостях x1 и x2 каждому направлению распространения волны со-
ответствует определенное направление круговой поляризации. При таком размещении ферритовой пластины и таком направлении распространения волны, как это указано на рис.10.5, в феррите будет правополяризованное поле и фазовая скорость будет определяться µ+ . Для волны, которая будет распространять-
ся в обратном направлении, поле в феррите будет левополяризованным и фазовая скорость будет определяться µ− . Поскольку µ+ и µ− имеют разные значе-
ния, то и фазовый сдвиг на единицу длины ферритовой пластины при прямом и обратном направлениях распространения волны будет разным, то есть невзаимным.
Ферритовые пластины ограниченной длины характеризуются дифференциальным (разностным) фазовым сдвигом ∆ϕ. С увеличением толщины пла-
