
- •Введение
- •Список сокращений
- •1. Линии передачи СВЧ
- •1.1. Основные положения
- •1.2. Коаксиальная линия передачи.
- •1.3. Двухпроводная линия передачи
- •1.4. «Витая пара»
- •1.5. Прямоугольный волновод
- •1.6. Круглый волновод
- •1.7. Планарные линии передачи
- •2. Теория длинных линий
- •2.1. Основы теории длинных линий
- •2.2. Нормированные значения напряжения
- •2.3. Коэффициент отражения
- •2.4. Нормированные сопротивление и проводимость
- •2.5. Интерференция падающей и отраженной волн в нагруженной линии
- •2.6. Входное сопротивление линии передачи с нагрузкой
- •2.7. Основные режимы работы линии передачи
- •2.8. Круговая диаграмма сопротивлений
- •2.9. Полуволновые и четвертьволновые трансформаторы
- •3. Согласование линий передачи
- •3.1. Общие положения теории согласования линий передачи с нагрузкой
- •3.2. Согласование с помощью четвертьволнового трансформатора
- •3.3. Согласование с помощью сосредоточенной реактивности
- •3.5. Согласование с помощью параллельного реактивного шлейфа.
- •3.6. Трансформаторы с тремя реактивными элементами.
- •4. Матричные методы описания устройств СВЧ
- •4.1. Матрицы рассеяния многополюсников
- •4.2. Волновые матрицы передачи многополюсников
- •5. Двухполюсники
- •5.1. Согласованные нагрузки
- •5.2. Реактивные нагрузки
- •5.3. Преобразователи СВЧ мощности
- •6. Четырехполюсники
- •6.1. Разъемы и соединения
- •6.2. Переходы между линиями разных типов
- •6.3. Нерегулярности в волноводе
- •6.4. Изгибы и скрутки волноводов
- •6.5. Аттенюаторы
- •6.6. Фазовращатели
- •6.7. Согласующие трансформаторы
- •7. Резонаторы и фильтры СВЧ
- •7.1. Объемные резонаторы
- •7.2. Основные типы резонаторов
- •7.3. Открытые резонаторы
- •7.4. Диэлектрические резонаторы
- •7.5. Резонатор, включенный на проход
- •7.6. Частотные фильтры
- •8. Шестиполюсники
- •8.1. Y-тройники
- •8.3. Шестиполюсные делители мощности
- •9. Восьмиполюсники и двенадцатиполюсники
- •9.1. Направленные ответвители
- •9.2. Мостовые устройства
- •9.3. Крестообразные соединения
- •9.4. Резонатор бегущей волны
- •9.5. Двенадцатиполюсники
- •10. Ферритовые устройства СВЧ
- •10.1. Основные свойства ферритов на СВЧ
- •10.2. Ферритовые устройства на эффекте Фарадея
- •10.3. Вентили с поперечно подмагниченным ферритом
- •10.4. Фазовые циркуляторы
- •11. Физические основы работы полупроводниковых приборов СВЧ диапазона
- •11.1. Энергетические зоны полупроводников
- •11.2. Процессы переноса заряда в полупроводниках
- •11.3 Полупроводники в сильных электрических полях
- •11.4. Контактные явления
- •12.1. Полупроводниковые аналоги вакуумных приборов СВЧ
- •12.2 Динамическая отрицательная проводимость
- •12.3. Лавинное умножение носителей заряда
- •12.4 Основные режимы работы ЛПД
- •12.5. Технический уровень промышленно выпускаемых ЛПД
- •13. Полупроводниковые приборы с объемной неустойчивостью (диоды Ганна)
- •13.1. Механизм междолинного перехода
- •13.2 Эффект Ганна и критерий Кремера
- •13.3 Динамика ганновских доменов
- •13.4. Классификация режимов работы генераторов Ганна
- •13.5. Предельные параметры генераторов Ганна
- •13.6. Способы повышения эффективности и верхнего частотного предела генераторов Ганна
- •14.1. Основы полупроводниковой технологии
- •14.2. Конструкции диодных СВЧ генераторов
- •14.3. Способы перестройки частоты
- •15. Повышение мощности полупроводниковых генераторов и освоение миллиметрового диапазона волн
- •15.1. Основные принципы построения СВЧ-сумматоров
- •15.2. Конструкции сумматоров мощности
- •15.3. Освоение миллиметрового и субмиллиметрового диапазонов
- •16. Усилители СВЧ
- •16.1. Основные параметры усилителей
- •16.2. Классификация усилителей СВЧ
- •16.3. Однокаскадный транзисторный усилитель
- •16.4. Принцип действия балансного усилителя
- •17. Преобразователи частоты
- •17.1. Смесители
- •17.2. Преобразование частот в смесителе
- •17.3. Основные параметры смесителей
- •17.4. Небалансные смесители
- •17.5. Балансные смесители
- •17.6. Двойные балансные смесители
- •17.7. Кольцевые балансные смесители
- •17.8. Транзисторные смесители
- •Тесты для самопроверки
- •Ответы на тесты
- •Библиографические ссылки
- •Список рекомендованной литературы
- •Предметный указатель
119
7.Резонаторы и фильтры СВЧ
7.1.Объемные резонаторы
Внизкочастотной радиотехнике одними из самых важных элементов являются колебательные (резонансные) контуры с сосредоточенными параметрами. Они состоят из конденсаторов и катушек индуктивности. Геометрические размеры этих элементов и соединительных проводников значительно меньше, чем длина волны колебаний. Потому такие контуры практически не излучают электромагнитную энергию. Добротность их обусловлена только тепловыми потерями в катушках и соединительных проводниках и потерями в диэлектрике конденсатора. С увеличением частоты геометрические размеры элементов контуров становятся соизмеримыми с длиной волны, что приводит к увеличению излучения. В СВЧ диапазоне вместо колебательных контуров применяются объемные резонаторы.
Объемным резонатором (англ. – cavity resonator) называют ограничен-
ный отражающими поверхностями объем, который имеет связь с внешним электромагнитным полем, обладает способностью накапливать электромагнитную энергию и характеризуется набором дискретных собственных частот. В общем случае резонатор можно образовать совокупностью металлических или диэлектрических тел, в средине или вблизи которых будет концентрироваться переменное электромагнитное поле. Свойства объемных резонаторов схожи со свойствами колебательных контуров. Благодаря высокой добротности в сантиметровом диапазоне (~103–104) объемные резонаторы применяются как вторичные эталоны частоты. Они являются основными элементами микроволновых генераторов, на их основе строят замедляющие системы и фильтры. При внесении в резонатор диэлектрического или магнитного образца изменяется его резонансная частота и добротность, на этом эффекте основывается определение диэлектрических и магнитных параметров материалов.
В теории объемных резонаторов различают режимы собственных (свободных) и вынужденных колебаний. Собственные колебания (англ. – natural oscillation, eigenmode) – это возможные поля в объемном резонаторе при отсутствии источников. Спектр собственных колебаний резонатора представляет собой бесконечное множество различных типов колебаний (типов полей), для каждого из них характерным является свое распределение электромагнитного поля и определенная собственная длина волны и собственная частота (англ. – natural frequency, eigenfrequency). В резонаторе без потерь (стенки идеально проводящие, отверстий в оболочке нет, внутренний объем заполнен идеальным диэлектриком) собственные колебания были бы незатухающими. В реальном объемном резонаторе всегда есть потери энергии, которые приводят к затухающим колебаниям.
Незатухающие колебания в реальном резонаторе могут существовать только в режиме вынужденных колебаний (англ. – forced oscillation), при кот о- ром в резонатор через элемент связи вводится энергия стороннего источника

120
(генератора). Для возбуждения резонатора необходимо, чтобы частота колебаний генератора была равна одной из резонансных частот (англ. – resonant frequency) объемного резонатора. В этом случае в резонаторе возникает резонанс и амплитуда поля вынужденных колебаний достигает наибольшего значения. В объемном резонаторе с малыми потерями (с большой добротностью) резонансные частоты приближенно равны собственным частотам этого резонатора без потерь. Объемный резонатор является многорезонансной системой в отличие от колебательного контура с сосредоточенными элементами, который резонирует только на одной частоте.
Простейшим объемным резонатором является отрезок регулярной линии передачи l , ограниченный с обоих боков отражающими стенками. Допустим, что в волноводе на частоте ω возбуждена волна определенного типа. Длину волны в волноводе определим выражением
Λ = |
|
λ |
|
= |
2π |
, |
(7.1) |
|
|
|
|
β |
|||||
1−(λ / λкр )2 |
||||||||
|
|
|
|
|
||||
где λ = λ0 

 εrμr – длина волны в среде; λ0 – длина волны в вакууме; εr , μr − относительные диэлектрическая и магнитная проницаемости среды; λкр – критическая длина волны; β– фазовая постоянная.
εrμr – длина волны в среде; λ0 – длина волны в вакууме; εr , μr − относительные диэлектрическая и магнитная проницаемости среды; λкр – критическая длина волны; β– фазовая постоянная.
Когда волна доходит до конца указанного отрезка, она отражается от стенки и распространяется в обратном направлении и, отразившись от другой стенки, интерферирует с первичной волной. Этот процесс повторяется многократно, результирующее поле образует стоячую волну. Если в результате интерференции амплитуда первичной волны увеличивается, то в отрезке волновода происходит накопление энергии, то есть наблюдается резонанс. Условием резонанса является синфазность первичной и двукратно отраженной волн. Последняя на своем пути получает фазовый сдвиг
φ = βl + φ1 +βl + φ2 , |
(7.2) |
где φ1, 2 – сдвиги фаз в результате отражения от стенок, которые зависят от типа
поляризации и равны 0 или π .
Таким образом, условие резонанса имеет вид
φ = 2βl + φ1 + φ2 = 2πs, |
s =1,2,.... |
(7.3) |
Взяв к сведению возможные значения φ1 |
и φ2 , преобразуем (7.3) к виду |
|
Λ = 2l / p , |
|
(7.4) |
где p = s − δ; δ = 0 или 1 в зависимости от типа поляризации волны. То есть индекс p принимает целое положительное значение, начиная с 0 или 1.
121
Таким образом, в случае резонанса на отрезке волновода l укладывается целое число p длин полуволн Λ 2, то есть l = p Λ
2, то есть l = p Λ 2. При этом значению p = 0
2. При этом значению p = 0
соответствует бесконечно большая длина волны в волноводе.
Объемные резонаторы рассмотренного типа могут быть реализованы на основе прямоугольных, круглых волноводов, коаксиальных и других линий передачи. Такие резонаторы еще называют закрытыми или полыми.
Если свернуть отрезок линии передачи в кольцо, получим так называе-
мый кольцевой резонатор, или резонатор бегущей волны (РБВ). Условием ре-
зонанса в таком резонаторе будет равенство фаз первичной волны и волны, которая обошла резонатор по периметру кольца. То есть, периметр кольца должен быть равен целому числу длин волн l = pΛ , p =1,2,.... В данном случае в резо-
наторе устанавливается режим бегущей волны.
Для описания свойств резонатора с потерями вводят понятие комплексной собственной частоты ω0 = ω′+ jω′′ (аналогичным образом можно ввести ком-
плексную резонансную частоту). Мнимая часть описывает затухание колебаний в резонаторе. Обычно ω′′ << ω′ и ω0 ≈ ω′.
Одним из основных параметров объемного резонатора является его добротность. Добротностью (англ. – quality, Q-factor) объемного резонатора на данном типе колебаний называют отношение действительной части собственной частоты к удвоенному значению мнимой:
Q = |
ω′ |
. |
(7.5) |
′′ |
|||
|
2ω |
|
|
Величину обратную добротности, которая определяет относительное уменьшение амплитуды колебаний за каждый последующий период, называют декре-
ментом затухания (англ. – decrement):
d = |
1 |
= |
2ω′′ |
. |
(7.6) |
Q |
′ |
||||
|
|
ω |
|
||
В случае малых потерь добротность резонатора можно определить по формуле (энергетическое определение добротности)
Q = 2πWз |
= ω |
Wз , |
(7.7) |
W |
0 |
P |
|
п |
|
п |
|
где Wз – запасенная при резонансе электромагнитная энергия; Wп – энергия полных потерь за период; Pп – средняя за период мощность полных потерь; ω0 – резонансная частота.
Добротность, которая зависит от мощности полных потерь, часто называют нагруженной (англ. – loaded) добротностью резонатора. Мощность полных потерь имеет вид
Pп = P0 + Pвн , |
(7.8) |

|
|
|
|
|
|
|
122 |
|
|
|
|
|
|
|
|
||
где P0 – |
мощность собственных потерь (непосредственно в резонаторе); |
Pвн – |
|||||||||||||||
мощность внешних потерь, которая определяется выходом энергии из резона- |
|||||||||||||||||
тора через элементы связи во внешнюю цепь. |
|
|
|
|
|
|
|||||||||||
|
Из (7.7) и (7.8) следует, что |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
1 = |
1 |
+ |
1 , |
|
|
|
|
|
(7.9) |
||
|
|
|
|
|
|
Q |
Q |
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
|
н |
|
0 |
|
|
вн |
|
|
|
|
|
|
причем Q0 называют собственной (англ. – unloaded, internal) добротностью ре- |
|||||||||||||||||
зонатора; |
Qвн |
– внешней (англ. – external) добротностью, обусловленной поте- |
|||||||||||||||
рями на элементах связи. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Собственную добротность можно определить следующим образом: |
|
|||||||||||||||
|
|
|
|
|
|
1 = |
1 |
|
+ |
1 , |
|
|
|
|
|
(7.10) |
|
|
|
|
|
|
|
Q |
Q |
|
|
|
Q |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
м |
|
|
д |
|
|
|
|
|
|
|
где Qм – добротность, обусловленная потерями в проводниках стенок резона- |
|||||||||||||||||
тора; Qд – добротность, обусловленная потерями в диэлектрике. |
|
||||||||||||||||
|
Коэффициент полезного действия (англ. – efficiency) резонатора равен |
||||||||||||||||
отношению мощности, которая излучается в нагрузку, к суммарной мощности |
|||||||||||||||||
потерь в резонаторе: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
η = |
Pвн |
|
= |
|
1 |
|
= |
1 |
|
. |
(7.11) |
|
|
|
|
|
|
|
P + P |
|
|
1+ P P |
|
1+Q Q |
|
|
||||
|
|
|
|
|
|
вн |
0 |
|
|
|
0 |
вн |
|
вн |
0 |
|
|
|
Величину κ = Pвн / Р0 = Q0 / Qвн называют коэффициентом связи (англ. – |
||||||||||||||||
coupling coefficient) резонатора. При κ =1 излучаемая в нагрузку мощность рав- |
|||||||||||||||||
на мощности, которая рассеивается в резонаторе. Такой режим называют кри- |
|||||||||||||||||
тическим (англ. – critically coupled). При этом нагруженная добротность в два |
|||||||||||||||||
раза меньше собственной добротности, |
то есть |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
Q = Q0 . |
|
|
|
|
|
(7.12) |
||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
При условии |
κ >1 |
излучаемая в нагрузку мощность превышает мощ- |
||||||||||||||
ность, которая рассеивается в резонаторе. Такой режим называют режимом пе- |
|||||||||||||||||
ресвязи (англ. – overcoupled). И, наконец, при слабой связи ( κ <1) потери мощ- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
ности в нагрузке меньше потерь мощ- |
||||||||
|
|
|
|
|
|
|
|
|
ности |
в |
резонаторе, |
возникает так |
|||||
R0 |
C0 |
L0 |
C0 |
R |
C |
L |
|
|
называемый режим недосвязи (англ. – |
||||||||
1 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
undercoupled). Нагруженная доброт- |
||||||||
|
а |
|
|
б |
|
|
|
|
ность при этом близка к собственной |
||||||||
|
|
|
|
|
|
|
добротности резонатора. |
|
|||||||||
Рис.7.1. Эквивалентная схема резонатора: |
|
|
|||||||||||||||
|
|
|
Резонаторы СВЧ имеют беско- |
||||||||||||||
|
|
а – общая схема; |
|
|
|
|
|
||||||||||
|
|
|
|
|
нечное |
количество |
собственных ча- |
||||||||||
|
б – схема нагруженного резонатора |
|
|
||||||||||||||
|
|
|
стот, однако вблизи определенной ре- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
123
зонансной частоты резонатор можно представить эквивалентной схемой в виде
параллельного или последовательного колебательного контура. При этом счи-
тают, что взаимодействие между соседними типами колебаний отсутствует. Выбор параллельной или последовательной схемы зависит от выбора плоскости отсчета фаз (эквивалентного представления параметров резонатора). Если в режиме расстройки (ω ≠ ω0 ) входное сопротивление Zвх → 0 в этой плоскости,
то следует пользоваться параллельной схемой, если Zвх → ∞ – последователь-
ной. На практике отдают предпочтение параллельному контуру (рис.7.1,а). Для выполнения эквивалентности необходимо, чтобы колебательные системы имели одинаковую резонансную частоту и одинаковую добротность, то есть
Q = |
C0 |
|
R = C R ω |
; |
L C ω2 |
=1. |
(7.13) |
|||||
|
||||||||||||
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
|
|
||
|
L0 |
|
|
|
|
|
|
|
|
|
||
С помощью этих двух уравнений, если известны параметры резонатора Q0 и ω0 , можно определить элементы эквивалентного контура R0 ,C0 , L0 с точ-
ностью до произвольной постоянной.
Теперь учтем внешние потери. Для этого допустим, что резонатор связан с линией передачи, которая согласована с нагрузкой. Заменим линию ее эквивалентом в виде единичного нормированного сопротивления. Тогда получим эквивалентную цепь (рис.7.1,б), элементы которой нормированы к волновому сопротивлению линии передачи. При этом выражения для добротности прини-
мают вид |
|
|
|
|
|
|
|
|
|
|
Q = CRω ; Q = C |
R |
|
ω |
; Q |
= Cω |
; LCω2 |
=1. |
(7.14) |
||
R +1 |
||||||||||
0 |
0 |
0 |
вн |
0 |
0 |
|
|
|||
Тогда коэффициент связи равен |
|
|
|
|
|
|
|
|
||
|
κ = Q0 / Qвн = R . |
|
|
|
(7.15) |
|||||
Таким образом, уравнения (7.14)–(7.15) определяют элементы эквива-
|
|
|
|
|
|
|
|
|
|
Γн |
|
|
|
|
|
arg(Γн ) |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
π
–π
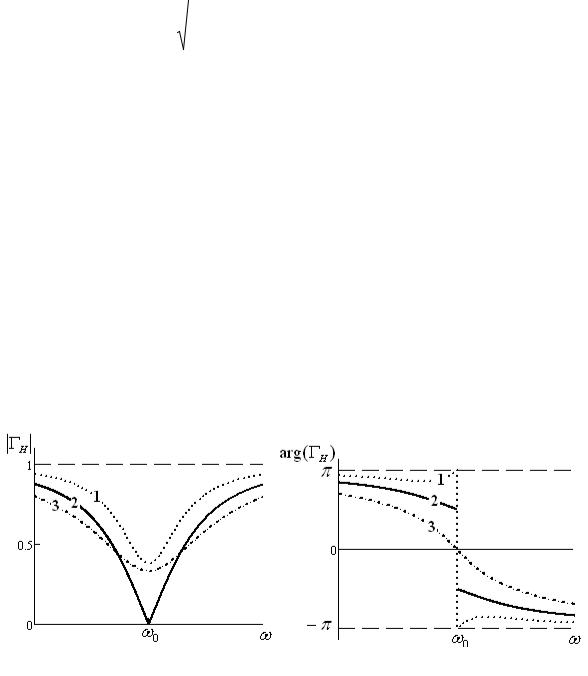
а |
б |
Рис.7.2. Частотные зависимости модуля (а) и фазы (б) коэффициента отражения
