116. Енергетичні зони в кристалах

Використовуючи рівняння Шредінгера – основне рівняння в нерелятивістській квантовій механіці, у принципі, можна розглянути задачу про кристал, наприклад, знайти можливі значення енергії, а також відповідні енергетичні стани електронів та ядер. Але як у класичній, так і у квантовій механіці відсутні методи точного розв'язання динамічної задачі для системи багатьох частинок. Тому цю задачу розв'язують наближено, зведенням задачі багатьох частинок до одноелекронної задачі – задачі про один електрон, що рухається в заданому зовнішньому полі. Цей шлях приводить до зонної теорії твердого тіла. В основі зонної теорії лежить адіабатичне наближення. Квантово-механічна система поділяється на важкі і легкі частинки - ядра і електрони. Оскільки маси і швидкості цих частинок значно відрізняються, можна вважати, що рух електронів відбувається в полі нерухомих ядер, а ядра, що повільно рухаються, знаходяться в усередненому полі всіх електронів. Вважаючи, що ядра у вузлах кристалічної ґратки нерухомі, рух електрона розглядається в постійному періодичному полі ядер. Далі використовується наближення самоузгодженого поля. Взаємодія даного електрона з усіма іншими електронами замінюється дією на нього стаціонарного електричного поля, що має періодичність кристалічної ґратки. Це поле створюється усередненим в просторі зарядом усіх інших електронів і ядер. Таким чином, багатоелектронна задача зводиться до задачі про рух одного електрона в зовнішньому періодичному полі - усередненому і узгодженому полі всіх ядер і електронів. Рівняння Шредінгера в цьому випадку набирає вигляду:

h ²/2m• + U( r )= E

д е U( r ) - потенціальна енергія одного електрона не лише в періодичному полі ядер ґратки, але і в усередненому періодичному полі всіх інших електронів.

І снують два наближені методи розв'язання цього рівняння. В першому з них передбачається, що енергія U( r ) мала, порівняно з повною енергією електронів Е. Це означає, що повна енергія електрона або, точніше, його кінетична енергія значно більша за його потенціальну енергію. Іншими словами, електрон є майже вільний, силове поле ґратки чинить на нього лише незначну збурюючу дію (метод слабкого зв'язку). В результаті розв'язування рівняння Шредінгера виявляється, що спектр можливих значень енергій валентних електронів розпадається на ряд дозволених і заборонених зон, які чергуються. В межах дозволених зон енергія змінюється квазі неперервно. Значення енергії, що належать забороненим зонам, не можуть реалізуватися .

У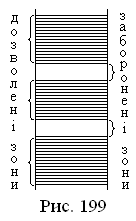 другому наближенні навпаки, вважається, що електрон сильнозв'язаний зі своїм атомом (ядром) і не може вільно переміщатися по ґратці (метод сильного зв'язку). Якісно задача розв'язується так. Із окремих атомів будується кристалічна гратка і з'ясовується, як впливають сусідні атоми кристала на поведінку електрона в окремому атомі, тобто досліджується вплив поля сусідніх атомів на енергетичні рівні.

В ідмінність між кристалом й атомом полягає в цьому випадку в такому: в той час як в ізольованому атомі даний енергетичний рівень Е_a(n,l) є єдиним, в кристалі, що складається з N атомів, він повторюється N разів. Кожний рівень ізольованого атома в кристалі N-кратно вироджений. У міру зближення ізольованих атомів і утворення з них ґратки кожний атом потрапляє у поле своїх сусідів, яке зростає. Така взаємодія приводить до зняття виродження. Тому кожний енергетичний рівень, не вироджений в ізольованому атомі, розщеплюється на N близько розміщених один від одного підрівнів, що утворюють енергетичну зону. На кожному підрівні згідно з принципом Паулі може знаходитись не більше двох електронів з антипаралельними спінами.

Найбільший вплив поле ґратки чинить на зовнішні валентні електрони атомів. Тому стани цих електронів у кристалі відчувають найбільші зміни, а енергетичні зони, які утворені з енергетичних рівнів цих електронів, виявляються найбільш широкими.

Внутрішні ж електрони, які сильно зв'язані з ядром, відчувають лише незначні збурення від інших атомів, внаслідок чого їх енергетичні рівні в кристалі залишаються практично такими ж вузькими, як і в ізольованих атомах. На рис. наведена схематична картина утворення енергетичних з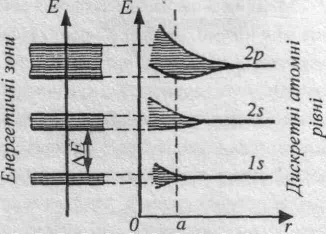 он в кристалі із дискретних атомних рівнів. Зони дозволених енергій розділені областями заборонених енергій - забороненими зонами E_з. Із збільшенням енергій електрона в атомі ширина дозволених зон збільшується, ширина

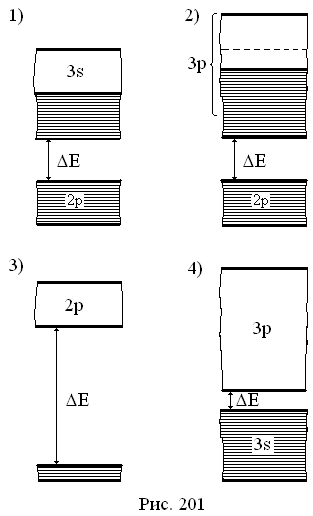заборонених - зменшується. Дозволені енергетичні зони в твердому тілі можуть бути різним чином заповнені електронами. У граничних випадках вони можуть бути цілком заповнені або цілком вільні. Електрони в твердих тілах можуть переходити з однієї дозволеної зони в іншу. Для переходу електрона з нижньої зони в сусідню верхню зону необхідно затратити енергію, що дорівнює ширині забороненої зони, яка розміщена між ними.

Д ля внутрішніх переходів електронів в межах зони необхідна досить мала енергія. Наприклад, для цього достатньо енергії 10^-4 – 10^-8eB, що отримує електрон в металі під дією електричного поля на довжині вільного пробігу при звичайних різницях потенціалів. Під дією спеціального збудження електронам може бути надана енергія, достатня як для внугрішньозонних, так і для міжзонних переходів.