57. Рівняння Максвелла для електромагнітного поля

Відкриття струму зміщення дало змогу Максвеллу створити єдину теорію електричних і магнітних явищ. Ця теорія пояснила всі відомі того часу експериментальні факти і передбачила ряд нових явищ, існування яких підтвердилось пізніше.

Рівняння Максвелла пов’язують змі­ни основних характеристик електромагніт­ного поля – векторів , , , в даному матеріальному середовищі з розподілом у ньому електричних зарядів і струмів.

Середовище в рівняннях Максвелла враховується феноменологічне, тобто без розкриття внутрішнього механізму взаємо­дії речовин з полем.

В основі теорії Максвелла лежать чотири рівняння.

1. Електричне поле може бути як потен­ціальним ( ) так і вихровим ( ). Тому напруженість сумарного поля .Оскільки циркуляція вектора по довіль­ному замкненому контуру дорівнює нулю, то циркуляція вектора сумарного поля

.

Це рівняння зв’язує значення із зміною вектора з часом і є виразом зако­ну електромагнітної індукції.

Перше рівняння Максвелла вказує на те, що джерелами електричного поля можуть бу­ти не тільки електричні заряди, але і змінні з часом магнітні поля.

2. Узагальнена теорема про циркуля­цію вектора :

.

Це рівняння показує, що магнітні поля можуть збуджуватись або рухомими заряда­ми, або змінними електричними полями.

3. Теорема Остроградського-Гаусса для потоку вектора електричного зміщення крізь довільну замкнену поверхню S , що охоплює сумарний заряд q:

.

Якщо заряд розподілений всереди­ні замкненої поверхні з об'ємною густи­ною , то

.

4. Теорема Остроградського-Ґаусса для магнітного потоку крізь довільну зам­кнену поверхню S:

.

Величини, що входять в рівняння Максвелла, не є незалежними і між ними є такий зв’язок:

, , .

Зазначимо, що до першого та четвер­того рівняння Максвелла входять лише основ­ні характеристики поля і , а в друге і третє – лише допоміжні величини і .

Рівняння Максвелла несиметричні відносно полів. Це зв’язано з тим, що в природі існують електричні заряди, а нема магнітних.

Для стаціонарних полів (Е=const і В=const) рівняння Максвелла мають та­кий вигляд:

, , , .

У даному випадку електричні і магніт­ні поля існують незалежно одне від одного.

58. Основні властивості електромагнітних хвиль

Згідно з теорією Максвелла змінне електричне і магнітне поле тісно взаємо­зв’язане, вони утворюють єдине електро­магнітне поле.

Джерелами електромагнітного поля служать різні змінні струми: змінний струм у провідниках, коливний рух іонів, електро­нів й інших заряджених частинок.

П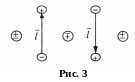 ростою системою, яка еквівалентна змінному струму, є електричний диполь з моментом, що гармонічно змінюється. В початковий момент заряди +q i -q такого диполя суміщені один з одним і тому p=0 (рис. 3). Через чверть періоду заряди роз­ходяться на максимальну відстань l, момент диполя максимальний і р=ql. Через півперіод заряди знову сходяться (р=0), а потім через розходяться в протилежні сторони на відстань l і р = -ql. Потім процес періодично повторюється.

Змінне електричне поле, яке виникає під час руху зарядів, породжує змінне магніт­не поле, а змінне магнітне поле створює змін­не електричне поле. Ці вторинні змінні поля мають вихровий характер. Отже, у просторі, який оточує заряди, виникає послідовність взаємних перетворень електричних і магніт­них полів, що поширюються від точки до точки. Цей процес буде періодичним у часі і просторі і, отже, є хвилею.

Електромагнітними хвилями назива­ються збурення електромагнітного поля, що поширюються у просторі.

З рівнянь Максвелла

,

можна отримати рівняння плоскої елек­тромагнітної хвилі.

Хвильове рівняння для Е_z має вигляд:

,

а для H_y:

.

Отже, змінне електромагнітне поле поширюється в просторі у вигляді електро­магнітної хвилі.

Фазова швидкість електромагнітних хвиль визначається виразом

,

де – електродинамічна стала.

Для вакууму і .

Оскільки , то швидкість по­ширення електромагнітних хвиль у речови­ні завжди менша, ніж у вакуумі.

Величина збігається зі швидкістю світла у вакуумі. Це привело Максвелла до думки про електромагнітну природу світла.

З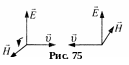 рівнянь Максвелла випливає висно­вок про те, що вектори і електро­магнітної хвилі завжди взаємно перпенди­кулярні. Крім того, вони лежать у площині, перпендикулярній до напрямку поширення хвилі, тобто до вектора швидкості хвилі. От­же, електромагнітні хвилі є поперечними.

Взаємна орієнтація трійки векторів , , задовольняє таке правило: з кінця вектора обертання від до по найкоротшому шляху виглядає таким, що відбувається проти руху стрілки годинника (рис. 4).

Розв’язками отриманих хвильових рівнянь є функції

, ,

де – циклічна частота хвилі, к – хвильове число, яке дорівнює , – початкові фази коливань в точках з координатою х=0.

Використовуючи хвильові рівняння для Е_z і Н_у і функції Е_z і H_y, можна показати, що

.

Отже, коливання електричного і маг­нітного векторів у електромагнітній хвилі відбувається з однаковою фазою – вони одночасно досягають максимальних значень і одночасно перетворюються в нуль, а амплітуди цих векторів зв’язані співвідношенням.

.

Р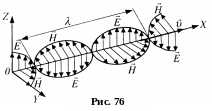 івняння плоскої електромагнітної хвилі у векторній формі має вигляд

, .

Косинусоїдальна електромагнітна хвиля називається монохроматичною хви­лею. В кожній точці електромагнітного поля ля монохроматичної хвилі проекції векторів та на осі координат інерціальної системи відліку здійснюють гармонічні коливання однакової частоти , яка називається частотою хвилі.

На рис. 5 наведені вектори і поля плоскої монохроматичної хвилі в один і той самий момент часу. У фіксованій точці простору вектори і змінюються з часом за гармонічним законом.

Довжина , період Т, частота і швидкість поширення електромагнітної хвилі зв’язані між собою співвідношеннями