8.4 Рівняння динаміки обертального руху

Знайдемо момент імпульсу твердого тіла відносно осі обертання Z. Спочатку для точки , масою :

; ;

, з врахуванням, що

Для всього тіла :

І

O

Використовуючи рівняння моментів

- так виглядає рівняння динаміки обертального

руху твердого тіла відносно не-

рухомої осі обертання.

Воно аналогічне рівнянню динаміки поступального руху :

;

У векторній формі рівняння динаміки обертального руху твердого тіла записується в такій формі :

;

8.5 Закон збереження момента імпульса

Якщо механічна система ізольована , то момент зовнішніх сил . Тоді із рівнянь моментів випливає :

Це і є рівняння , що виражає закон збереження момента імпульса .

Якщо момент зовнішніх сил відносно нерухомої осі обертання тіла тотожньо рівний нулю , то момент імпульса тіла відносно цієї осі не змінюється в процесі руху.

Звідси випливає закон збереження момента імпульса :

Момент імпульса замкнутої (ізольованої) системи матеріальних точок тіл залишається постійним.

Момент імпульса зберігається також і для незамкнутої системи , якщо сума моментів зовнішніх сил дорівнює нулю.

9. Пружні напруження. Закон Гука. Деформація стрижнів

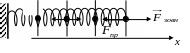
Всі реальні тіла під дією прикладених сил змінюють свою форму та об’єм, тобто деформуються. Для твердих тіл розрізняють два граничних випадки деформацій – пружні та пластичні. Пружною називають деформацію, яка зникає після припинення дії прикладених сил. Пластичними називають деформації, які повністю або частково зберігаються після припинення дії зовнішніх сил. Чи буде деформація пружною, чи пластичною – залежить не тільки від природи сили, але і від величини прикладених сил. Якщо сила не перевищує певної межі, яку називають межею пружності, то деформація буде пружною. Поділ тіл на пружні та пластичні – є умовним. Всі деформації реальних тіл являються пластичними.

При пружних деформаціях зовнішні прикладені сили врівноважуються результуючою внутрішньою пружною силою F_пр, які виникають у тілі в будь-якому перерізі. Внутрішні сили характеризуються механічною напругою:

(1)

, k –жорсткість (2)

Одним із найпростіших видів деформацій є деформація розтягу або стиску.

При цьому тіло зазнає зміни довжини. Якщо перед деформацією довжина стрижня , а після – , то називається абсолютною деформацією. Для розтягу , для стиску - .

Мірою деформації є відносна деформація, яка визначається :

.

Е

(3)

кспериментально встановлено, що для незначних пружних деформацій механічна напруга пропорційна абсолютній деформації :

,

де k – коефіцієнт пропорційності, який залежить як від матеріалу, так і від довжини стрижня. Якщо розрізати стрижень на дві рівні частини, то k збільшиться у два рази. Таким чином можна записати, що

(4)

,

де Е – величина, яка характеризує пружні властивості матеріалу стрижня і зветься модулем Юнга.

.

Тоді формула (3) з врахуванням формули (4) набуває вигляду :

(5)

,

Формула (5) виражає закон Гука :

відносне видовження стрижня прямо пропорційне механічній напрузі і обернено пропорційне модулю Юнга.

При деформації розтягу або стиску відбувається зміна поперечних розмірів тіл.

Відносний поперечний стиск (розтяг) :

розмірів тіла

, де - абсолютна зміна поперечних

деформації

- поперечний розмір тіла до

Відношення відносної поперечної деформації до відносної повздовжньої називають коефіцієнтом Пуассона :

, .

та завжди мають різні знаки (при розтягу додатнє, а - від’ємне).При деформації твердих тіл закон Гука виконується до певної межі:

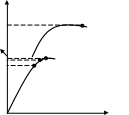
- межа пропорційності ;

- межа пружності ;

- межа текучості ;

. межа міцності.

Лекція №5