2.2.Пуассоновский импульсный процесс

Рассмотрим функцию (t) случайных величин_i,_i,вида

, (2.0)

сделав следующие предположения: 1)функцияF() затухает достаточно быстро, то естьF(||)0; 2)все_iи_iстатистически независимы между собой и их распределение не зависит от номера импульсаi,то есть 2n-мерная функция распределения системы распадается на сомножители

;

3)вероятность появления импульса в промежутке времени отtдоt+dtне за­ви­сит от времениtи числа предшествующих импульсов и пропорционально ин­тер­ва­луdt:

dP = dt,  = const. (2.0)

Естественно, что дифференциал – только линейная часть в вероятности Р,при достаточно больших интервалахdtлинейная зависимость (2.6)нарушается, так какdP1 всегда.

Найдем теперь вероятность P(n,t) появленияnимпульсов за промежуток времени от 0доt. Это событие (nимпульсов за интервал времениt)можно представить как сумму двух несовместимых событий: 1)за интервалt–dtпо­я­ви­лосьnимпульсов, а за интервалdt –ни одного; 2)за интервал t–dtпоявилосьn– 1 импульсов, а за интервалdt –один импульс. Для достаточно малого интервалаdtможно пренебречь вероятностью появления в нем двух и более импульсов. Тогда с учетом условия (2.6)можно записать:

P(n, t) = P(n, t – dt)(1 – dt) + P(n – 1, t – dt)dt.

Полагая P(n,t–dt) = P(n,t) – [P(n,t)/t]dt, получим, переходя к пределуdt0,

P(n, t)/t = [P(n – 1, t) – P(n, t)].

Введем производящую функцию и преобразуем уравне­ние, домножив его наsⁿи просуммировав поn,к виду

G(s, t)/t = (s – 1)G(s, t). Его решение

.

Поскольку, естественно, P(0, 0) = 1, P(n  1,0) = 0, тоG(s, 0) = 1. Поэтому

P(n,t) =e^–t (t)ⁿ/n!. (2.0)

Распределение (2.7)при <n> = tсовпадает с распределением Пуассона (1.7),то есть среднее число импульсов за интервал наблюденияtпро­пор­ци­о­нально длительности этого интервала. Естественно, распределение(2.7)не зависит от выбора начального момента, можно взять не 0, а произвольный моментt₁. Соответственно, вероятность того, что за интервал времениtне появилось ни одного импульса равнаP(0, t) = e^–t. Тогда вероятность того, что интервалмежду дву­мя соседними импульсами лежит междуtиt+dtесть произведение веро­ят­но­с­тей двух независимых событий –того, что за времяtимпульсов не было, и того, что за времяdtпоявился один импульс:

P{tt+dt} =(t)dt=e^–tdt, или (t) =e^–t. Тогда для среднего интервала между импульсами получаем:

.

Это соотношение позволяет определить каксреднюючастотупов­то­ре­ния импульсов.

Физически наблюдаемое условие (2.6)существования пуассоновского рас­пре­деления (2.7)эквивалентно предельному переходу в задаче Бернулли. Разобьем интервал наблюденияtнаNпромежутков=t/N. Тогда при большомNв силу условия (2.6)вероятность появления импульса на промежутке составляетp==t/N, то естьpN=const=t= <n>. Выберем теперь интервал наб­лю­де­ния Т, 0tT много большим как 1/, так и длительности одного им­пульса, то естьF(T) = 0. При этом импульсы, появившиеся за пределами интер­вала наблюдения, не вносят вклад в величину (t)и можно пренебречь краевыми эффектами –учетом или неучетом тех импульсов, которые срезаются концами интервала. Заметим, что момент появления импульса_iне обязательно соответствует началу импульса, он может соответствовать максимуму (для импульса F() = e^–||/)или другой определенной точке импульса.

Найдем распределение (x) случайной величины(t),то есть вероятность событияB,заключающегося в том, чтоx(t)x+dx:

P{B} =P{x(t)x+dx} =(x)dx.

Событие Вможет реализоваться в результате появления за интервал наблюденияTлюбого числа импульсов. Появление различного числа импульсов – события несовместимые, а какого-то числа–достоверное, то есть по формуле полной вероятности (1.4)получаем:

, (2.0)

где (x|n) –условное распределение вероятности величины(t)при условии того, что за время Tпоявилосьnимпульсов.

Следовательно, для моментов случайной величины (t)получаем:

, (2.0)

где m_k(|n)– условный момент случайной величины(t)при условии появления за интервалTровноnимпульсов. Но в соответствии с определением (2.5)слу­чай­ной величины(t)и в силу независимости случайных величин_iи_iполучаем:

Здесь – среднее значение_i, не зависящее от i.

Распределение _(t_i) момента появленияi-го импульса равномерное и нор­ми­ровано к 1на интервале от 0доТ, так как мы учитываем в условном распределении только импульсы, появившиеся на этом интервале, то есть

_(t_i) = 1/T. Тогда

. (2.0)

Здесь при переходе к бесконечным пределам мы учли, что F(||)0 достаточно быстро. С учетом соотношений (2.7)и (2.10)из уравнения (2.9)находим:

. (2.0)

Аналогично выводу соотношения (2.10)можно получить:

.

В силу взаимной независимости случайных величин _iи_iимеем:

То есть

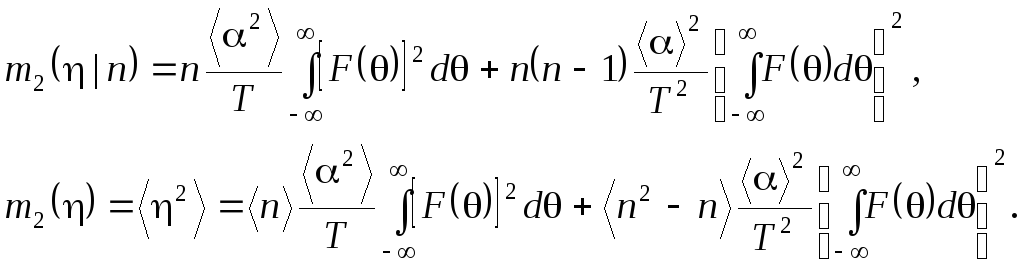
Учитывая, что для распределения Пуассона (2.7) <n²> = <n>²+ <n>, и соотношение (2.10),получим:

,

то есть

. (2.0)

В частном случае, если все импульсы одинаковы, то есть _i=a, то

–теоремаКемпбелла.

Рассмотрим теперь задачу о дробовом эффекте. Пусть электроны вы­ле­та­ют из нагретой нити-катода независимо друг от друга и летят на анод, веро­ят­ность вылета электрона за малый интервал времени dtсоставляетdP=dt, и пустьF() описывает импульс тока, связанный с пролетом одного электрона от катода к аноду. Тогда анодный ток –пуассоновский случайный импульсный процесс вида (2.5). ПоложимF(0) = 1,F(>) =F(< 0) = 0, где –время пролета электрона от катода до анода. Тогда a = e/, ,. Из теоремы Кемпбелла получаем:

.

Следует, однако, отметить, что любой измерительный прибор регистрирует не мгновенное значение тока i(t), а усредненную по некоторому интервалу времениT>>величину

.

Из-за независимого характера вылета электронов случайные величины i_kнезависимы, тогда

.

Найдем теперь характеристическую функцию пуассоновского случайного импульсного процесса вида (2.5 в новых лекциях 2.4).Поскольку в силу сделанных предположений все слагаемые в сумме (2.5)независимы, то условная характеристическая функция случайной величины(t) при условии, что за интервал наблюдения Tпоявилось nимпульсов, будет равна произведению характеристических функций слагаемых:

. (2.0)

Взяв преобразование Фурье от соотношения (2.8),получим связь между условными и безусловной характеристическими функциями случайной величины:

.

Подставляя в это соотношение выражение (2.13)для_(u|n) и формулу(2.7)дляP(n), получим:

или, переходя к бесконечным пределам по , для логарифма характеристической функции получим:

.

Таким образом, с учетом соотношения (1.22)для семиинвариантов характеристической функции получаем выражение

.

Найдем условия, при которых можно пренебречь третьим и старшими семи­ин­ва­ри­антами:

,

где  –длительность импульса. Таким образом, при выполнении условия

 >> 1, (2.0)

|₃| <<³, и всеми семиинвариантами старше второго можно пренебречь. При этом распределение вероятностей случайной величины(t) должно быть близко к нормальному вида (1.8),причем среднее значение и дисперсия определены соответственно соотношениями (2.11)и (2.12).

Заметим, что  –средняя частота следования импульсов, поэтому условие (2.14)означает, что импульсы должны густо перекрываться, то есть число толчков за время длительности одного импульса должно быть велико, и в силу центральной предельной теоремы распределение близко к нормальному.