6. Нелинейные преобразования случайных процессов

6.1.Нелинейное безинерциальное преобразование

Безинерциальнымназывается устройство, в котором связь между мгновенными значениями входного и выходного процессов является чисто алгебра­и­ческой:

(t) = f[(t)]. (6.0)

Многие реальные нелинейные устройства нельзя считать безинерциальными, од­нако их можно представить в виде двух последовательно соединенных частей: безинерциальногонелинейногоэлемента НЛ (6.1) и линейного инерциаль­ного элемента – фильтра Ф с амплитудно-частотной характеристикойk(), при­­чем обе части, линейную и нелинейную, можно о допустимой точностью считать развязанными, то есть их элементы можно рассматривать по отдельности.

В качестве примера рассмотрим умножение частоты (генерация гармоник). Предполагаем, что для генерации m-й гармоники используется нелиней­ностьn-й степени, то есть зависимость (6.1) имеет вид:

(t) = [(t)]ⁿ, (6.0)

а входной процесс представляет собой узкополосный случайный процесс

. (6.0)

Будем считать, что фильтр, настроенный на частоту m₀, имеет достаточно большую полосу пропускания,так что инерциальность фильтра никак не влияет на форму m-й гармоники, но при этом<<₀, то есть соседние гармоники через фильтр не проходят.

Подставляя соотношение (6.3)в формулу (6.2),получим:

. (6.0)

Из формулы (6.4)видно, что с помощью нелинейности четной степени(n = 2k)можно генерировать только четные гармоники, а при нелинейности нечетной степени (n = 2k + 1) –только нечетные,m-я гармоника на выходе фильтра описывается выражением . Средняя ин­тен­сивность этого процесса составляет

, (6.0)

где .

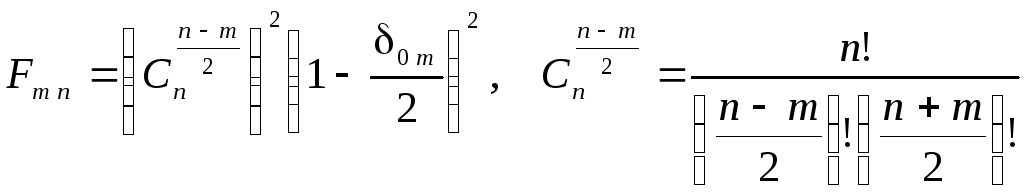Из формулы (6.5)видно, что от статистики входного процесса(6.3)форма спектра выходного процесса (6.4),то есть относительное распределение интенсивности процесса(t) по гармоникам, не зависит, она определяется факторомF_{m n}и уменьшается с ростомmпри заданной степени n. Величина же КПД генерации гармоники существенно зависит от статистики огибающей(t) входного процесса (6.3).Обозначая интенсивность входного колебания

²=²=²/2, найдем, что при гармоническом возбуждении ((t) =const,(t) =const)²ⁿ=²ⁿ2ⁿ, а при возбуждении стационарным гауссовым шумом с релеевским распределением амплитуды вида (5.18)с учетом формулы (5.19) ²ⁿ=n!²ⁿ2ⁿ. Таким образом, при одинаковых интенсивностях входных колебаний КПД генерации любой гармоники при гауссовом возбуждении вn! раз больше. Этот выигрыш связан с тем, что нелинейность "подчеркивает" выбросы случайного процесса.

6.2.Корреляционные функции на выходе умножителя частоты

Рассмотрим теперь спектральную плотность интенсивности G_m()m-й гармоники. В соответствии с формулами (6.5)и (4.5)получаем:

.

Предположим, что процесс (6.3) –узкополосный стационарный гауссов про­цесс с корреляционной функцией_=В() =²R(). Тогда корреляционная функция выходного процесса_=ⁿ_ⁿможет быть представлена в виде конечного ряда по степенямR():

(6.0)

Здесь ,

.

В соответствии с формулой (5.13)коэффициент корреляции для узкополосного случайного процесса (6.3)можно представить в виде, аналогичном (6.3):

R() = p()cos(₀) – q()sin(₀) = Q()exp(i₀) + Q^*()exp(–i₀). (6.0)

Тогда можно, воспользовавшись формулой (6.4),а для четногоsс учетом формулы (6.7),получить:

.

Подставляя это выражение в формулу (6.6),получим:

.

Изменяя порядок суммирования, получим:

, (6.0)

где .

Такая же формула получается и для нечетного n, но суммирование идет по нечетнымт= 1, 3, …п. Сравнивая формулы (6.7)и (6.8),видим, что функция автокорреляцииm-й гармоники определяется выражением:

B_m() = Q_m()exp(im₀) + Q^*_m()exp(–im₀). (6.0)

Спектральную плотность G_m() интенсивностиm-й гармоники можно найти, взяв Фурье-преобразование вида (4.3)от выражения(6.9).Если спектральная плотность интенсивностиG⁺() входного процесса (6.3)симметрична относительно частоты₀, то в соотношении (6.7)q() = 0 иQ() =p()/2, то есть Q()–вещественная функция (ср. 5.16).Тогда в формулу (6.8)входит величина, при этом Q_m()–вещественная и четная функция, так какp() =p(–). Следовательно, спектральная плотность интенсивностиm-й гармоники симметрична относительно частотыm₀.

Из соотношения (5.11)видно, что функцияp() имеет смысл коэффициента корреляции квадратурных компонент, то есть |p()|1, но в сумму (6.8)эта функция входит в степенях больших или равныхm, поэтомуQ_m() с ростомбудет уменьшаться не медленнее, чемр^m(). Если определить время корреляции входного процесса (6.3)соотношением , то для аналогичной оценки времени корреляции гармоники получим:

, (6.0)

то есть , соответственно_m. Вообще, при любом виде корреляционной функцииp() величина интеграла тем меньше, чем большеm. Поэтому формула (6.10)позволяет сделать вывод, что чем выше номер гармоникиm,тем шире ее спектр, так как_m~ 1/_K^(m)см. (4.8).

Рассмотрим для примера генерацию высшей гармоники, то есть m=n. Тогда в сумме (6.8)остается только один член, и из формулы (6.9) следует:

B_n() = 2^{–n + 1}a_npⁿ()cos(n₀).

Корреляционная функция входного процесса (6.3)определяется выражением (5.11): B() = ²p()cos(₀). Исходя из формулы (5.17)для симметричной спектральной плотности интенсивности входного процесса, получаем, так как

p() =p(–):

.

Соответственно спектральная плотность интенсивности п-й гармоники, симме­т­ричная относительно частотыn₀, определяется выражением

.

Так, если p() =exp(–||), то –лоренцева линия,

–тоже лоренцева линия. Еслиp() =exp(–²²), то

– гауссова линия, – тоже гауссова линия. Таким образом, если спектр входного процесса –лоренцев, то

спектр n-й гармоники –тоже лоренцев, но вnраз более широкий. Если спектр входного процесса гауссов, то спектр гармоники тоже гауссов, но уширение составляет, то есть меньше, чем для лоренцевой линии.