11. Флуктуации в лазерных системах

11.1.Корреляционная функция одномодового лазерного излучения

Рассмотрим квазимонохроматический (узкополосный) лазерный сигнал

E(t) =a(t)exp(it+i(t)), гдеa(t) – случайная амплитуда, обусловленная флуктуациями коэффициента усиления активной среды,(t) – случайная фаза, обусловленная изменением показателя преломления среды, длины резонатора и так далее. Амплитудные флуктуации часто удаётся уменьшить до 1 … 5%, поэтому в первом приближении можно положитьa(t) =a₀=constи записать лазерный сигнал в виде (5.20):

E(t) = a₀exp(it + i(t)). (11.0)

В силу центральной предельной теоремы (см. п. 1.7)и произвольности выбора начальной фазы, можно считать, что фаза(t), зависящая от многих независимых факторов, имеет нормальное распределение вида (1.8)с нулевых средним. По такому же нормальному закону с нулевых средним будет распределение и случайная величина_(t) =(t+) –(t) – набег фазы за время:

,

где

, (11.0)

– дисперсия случайной фазы,R_()–её коэффициент корреляции.

Если процесс E(t) стационарный, коэффициент его корреляции с учётом соотношений (11.1)и (11.2)можно записать в виде

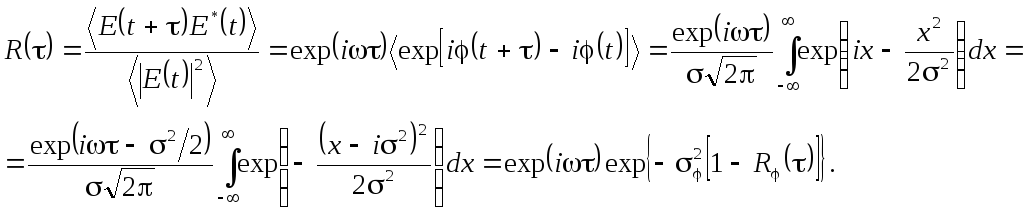(11.0)

Формула (11.3)аналогична выражению для функции автокорреляции действительного колебания с флуктуирующей частотой (см. п. 5.4),поэ­то­му спектральную интенсивность процессаE(t) можно оценить по формуле (5.22).

11.2. Корреляционная функция многомодового лазера

Пусть лазерный сигнал содержит 2N+ 1 мод с различными частотами_m, для каждой моды применима модель (11.1), тогда в качестве обобщения релеевской модели (7.16)можно принять

.

Пусть фазы _m(t) и амплитудыa_mмод статистически независимы, тогда

.

В силу независимости фаз разных мод

,

поэтому с учётом соотношения (11.3)получаем

.

Пусть все _m=_иR_m=R_, а_m=₀+m, тогда

, (11.0)

где R() –коэффициент корреляции центральной моды приm= 0.

Если Nочень велико, а ,то пределы суммирования можно рас­про­странить до бесконечности, при этом соотношение (11.4)оказывается рядом Фурье некоторой периодической функции F() с периодом 2/, следовательно, . И, наконец, для импульсного многомодового излучения . Для короткого импульсаa(t) можно считать фазы мод_mпостоянными и аналогично соотношению (11.4),положивR() = 1,получаем

.

Таким образом, для описания флуктуаций в многомодовом лазере необходимо найти корреляционную функцию одномодового.

11.3.Флуктуации в одномодовом лазере

С учётом потерь в резонаторе электромагнитное поле в лазере описывает­ся уравнением

. (11.0)

Heрассматривая поперечную структуру луча, ищем решение уравнения (11.5)в виде суммы мод (собственных функций резонатора):

, (11.0)

где k_q=q/l– волновое число,l– длина резонатора,q– целое. Подставляя соотношение (11.6)в уравнение (11.5),умножая его наsin(k_nz) и интегрируя по z от 0 до l,получим с учётом ортогональности собственных функций:

, (11.0)

где _n=ck_n –частотаn-йпродольной моды,– прос­т­ран­с­твенная Фурье-компонента поляризации.

Если процесс P_n(t) квазигармонический (узкополосный) со средней частотой_n, то можно положить (см. п. 5.3 ) , и уравнение (11.7)принимает вид

, (11.0)

где Q_n=_n/(2)–добротностьn-й моды резонатора. ЕслиE_n(t) =cos(_nt+_n) – узкополосный процесс (см. 5.7 – 5.9),то поляризация P_n(t), создаваемаяn-й модой, в рамках метода гармонического баланса может быть записана в виде:

P_n(t) = [Re() + ²Re()]cos(_nt + _n) + [Im() + ²Im()]sin(_nt + _n),

где –линейная,– нелинейная восприимчивость среды.

Для моды, приходящейся на середину линии люминесценции, Re() = 0,Re() = 0, и уравнение (11.8)принимает вид, близкий к уравнению(8.10):

, (11.0)

где обозначено = –2₀Im(),= 2₀Im(). В правой части уравнения (11.9),так же как и при описании флуктуаций вLC-генераторе (см. п. 7.3),учтена случайная внешняя сила(t), обусловленная флуктуациями –тепловыми шума­ми резонатора _T(t) и спонтанным излучением активной среды_С(t), причём обе случайные силы полагаются независимыми и дельта-коррелированными:

. (11.0)

Для того чтобы найти спектральную плотность интенсивности тепловых флу­ктуаций в самом резонаторе, положим в уравнении (11.9)== 0 (пассивный резонатор):

.

Это уравнение описывает воздействие случайного процесса _T(t) на линейную систему второго порядка с частотой характеристикой

. (11.0)

Тогда в соответствии с соотношением (5.3)получаем:

.

При этом средняя энергия одной моды резонатора в окрестности частоты равна (см. 4.5):

.

Сдругой стороны, в состоянии термодинамического равновесия с учётом распределения Планка приħ₀>kTполучаем

,

где n– среднее число фотонов в моде. Сравнивая эти выражения, находим спектральную интенсивность тепловых флуктуаций резонатора:

. (11.0)

Спектральную же интенсивность G_C(₀) флуктуаций среды определим как эквивалентный тепловой шум активной (< 0) среды с отрицательной тем­пе­ратуройT^*, соответствующей инверсной заселённости:

,

где N₁иN₂– заселённости верхнего и нижнего уровней,g₁иg₂– их кратности. За­меняя в уравнении (11.12)на –(отрицательное поглощение) и T наT^*, получим:

.

Учитывая, что вблизи порога генерации ,для спектральной интенсивности флуктуаций(t) вблизи частоты₀получим:

. (11.0)

Если в уравнение (11.9)подставить решение в форме узкополосного процесса (5.9),считаямедленно меняющейся амплитудой, и опустить быстро осциллирующие с частотой₀члены, то получим укороченные уравнения (ср. п. 8.3):

, (11.0)

где – медленно меняющаяся комплексная амплитуда флуктуаций в высокодобротном резонаторе, то есть

.

Поскольку частотная характеристика системы (11.10),формирующей узкополосный процесс (t),симметрична относительно частоты₀,то и спектральная интенсивностьG_() симметрична относительно частоты₀,тогда, полагая в формуле(5.16)  = 0 из-за дельта-коррелированности процесса_T(t)и подставляя в уравнение (5.17)комплексную амплитуду в виде, получим с учётом соотношения (11.10):

. (11.0)

Учитывая, что (см. п. 5.3),подставляя это значение в уравнение (11.14)и разделяя мнимые и действительные части, получим систему уравнений, эквивалентную исходному уравнению (11.14):

, (11.0)

. (11.0)

В отсутствие флуктуаций получаем , то есть из уравнения (11.16) следует, что, гдеР=––параметр предельного цикла,=/– параметр накачки,– характерная амплитуда. Соответственно, из уравнения (11.17)получаем(t) =₀=const, как и следовало ожидать в установившемся режиме без флуктуаций.

В присутствии флуктуаций уравнения (11.16)и (11.17)образуют связанную систему. Введём флуктуации амплитуд в установившемся режиме. Если,можно линеаризовать уравнения и с помощью достаточно громоздкой процедуры расщепить их:

, (11.0)

. (11.0)

Здесь _(t) и_(t) описывают флуктуационные составляющие правых частей уравнений (11.16)и (11.17)соответственно, причём, как следует из уравнения (11.15):

. (11.0)

Решение уравнения (11.18)при нулевых начальных условиях имеет вид:

.

В стационарном случае для t  получаем с учётом формулы (11.20):

. (11.0)

Спектральная плотность интенсивности амплитудных флуктуаций с корреляционной функцией вида (11.21)имеет лоренцову форму:

. (11.0)

Из уравнения (11.19)следует, что

,

то есть (t)–случайный процесс с независимыми приращениями как интеграл от дельта-коррелированного процесса (см. п. 8.2).Как следует из соотношения (8.6),его дисперсия пропорциональна времени:

. (11.0)

Поскольку (t) – нормальный процесс, его функция распределения описывается формулой (1.10),то есть

.

Таким образом, процесс (t)–марковский, для него определимы все конечномерные распределения и моменты, в частности коэффициент автокорреляции фазыR_(),что позволяет с помощью формулы (11.3)найти коэффициент автокорреляции процесса E_n(t), оценить его интервал корреляции_kи найти ширину полосы спектральной интенсивности процессаE_n(t) (см. п. 4.2).

Если пренебречь флуктуациями амплитуды, то с учётом соотношения (11.13) получаем:

, (11.0)

где _р=/– ширина линии пассивного резонатора,– мощность, излучаемая средой, идущая как на компенсацию потерь, так и на излучение. Формула (1.24), описывающаяестественнуюширинулиниилазерного излучения, называетсяформулойТаунсена.