1.6. Характеристическая функция. Семиинварианты

Характеристической функциейслучайной величиныназывается среднее значение случайной величиныexp(iu):

. (1.0)

То есть характеристическая функция является Фурье-образом функции распределения. Соответственно

. (1.0)

Заметим, что характеристическая функция, вообще говоря, комплекснозначна и ограничена по модулю:

.

Для среднего значения произвольной функции F() случайной величиныможно получить:

,

где – Фурье-образ функцииF(x).

Характеристическая функция (1.19 в новых лекциях 1.23)также однозначно описывает рас­пре­­де­ление вероятностей, как и функция распределения(х), и позволяет найти все моменты:

.

Разлагая экспоненту в формуле (1.19 в новых лекциях 1.23) в ряд по степеням х,получим:

. (1.0)

Величину логарифма характеристической функции (1.19 в новых лекциях 1.23) аналогично соотношению(1.21)также можно разложить в ряд Тейлора по степеням (iu):

. (1.0)

Коэффициенты _nразложения (1.22)называютсясемиинвариантами. Семи­ин­ва­ри­анты _n n-го порядка являются рациональной функцией n первых моментов слу­чайной величины:₁=m₁,₂=M₂=²,₃=M₃,₄=M₄– 3M₂².

Для нормального распределения вида (1.8)характеристическая функция то­же имеет нормальный вид: (u) = exp(ium₁() – ²u²/2),а все семиинварианты, начиная с третьего, равны нулю. Нетрудно показать, что характеристическая фун­­кция суммы двух независимых случайных величин равна произведению хара­­к­теристических функций этих величин, а семиинварианты суммы неза­виси­мых слу­чайных величин равны сумме семиинвариантов этих величин. Если=+,то

,_m() =_m() +_m().

Поскольку Фурье-образ произведения равен свёртке Фурье-образов со­мно­жителей, легко получить функцию распределения суммы двух независимых слу­чай­ных величин и:

. (1.0 в новых лекциях 1.27)

Получить непосредственно эту формулу композиции (1.23)трудно.

Для многомерной случайной величины можно ввести многомерную характеристическую функцию

.

1.7.Центральная предельная теорема

Понятие характеристической функции очень плодотворно. Тот факт, что характеристическая функция суммы независимых случайных величин равна произведению их характеристических функций, позволил Ляпунову доказать чрезвычайно важное для статистической радиофизики утверждение, получившее название центральнойпредельнойтеоремы.

Пусть ₁, …, _N –независимые случайные величины, <_i> = a_i,

M₂(_i) = _i² < C < . Если для любого> 0

,

то случайная величина имеет распределение, равномерно стремящееся к нормальному приN, независимо от распределения слагаемых.

Приведём доказательство центральной предельной теоремы для частного случая одинаково распределённых случайных величин _i с одинаковыми средними <_i> = aи конечной дисперсией², например длявыборки одной случайной переменной(t).Пусть _i = _i – a, тогда , <_N> = 0, , где . Сучётом формулы (1.21)получим выражение для характеристической функ­ции случайной величины_N:

.

Используя соотношение (1.20 в новых лекциях 1.24),получаем:

.

Для случайной величины _N=_N+aпри этом получаем

.

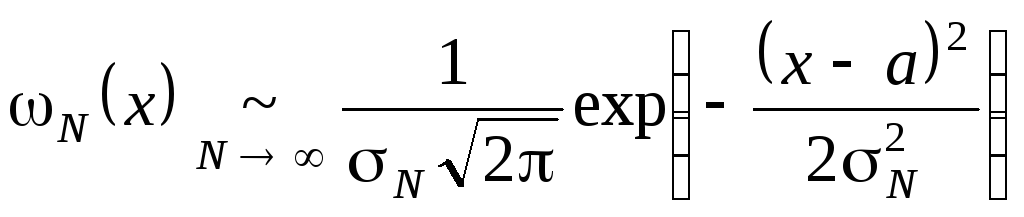То есть распределение выборочного среднего случайной величины сходится равномерно к нормальному с тем же средним значением и дисперсией, в Nраз меньшей. Отметим, что конечность дисперсий независимых случайных величин – необходимое условие центральной предельной теоремы. Так, например, дляраспределенияКошине существует моментов ни второго, ни всех чётных порядков. Его характеристическая функция(u) =exp(–|u|).Для суммы N независимых случайных величин_i, распределённых по Коши,

_N(u) = [(u)]^N = exp(–|Nu|). Следовательно,,

aдля нормированной суммы, независимо отN, , то есть снова распределение Коши, а не нормальное.

Заметим также, что часто для выполнения условий центральной пре­дельной теоремы достаточно некоррелированности (а не независимости) случайных величин_i,и даже условия, что

(1.0)

достаточно быстро. Например, можно взять, где_k –независимые случайные величины. Естественно, что при |i–j| <mвеличины_iи_jзависимы, причём выполняется условие(1.24).Но сумма_Nможет быть записана в виде суммы независимых случайных величин_kс некоторыми конечными коэф­фи­ци­ен­тами, поэтому центральная предельная теорема выполняется.