1.5.Совместные распределения. Условные функции распределения

Рассмотрим две зависимые случайные величины и. Пусть событиеАзаключается в том, чтох,а событиеВ –в том, что у. Тогда можно рассмотреть вероятность событияАВ: P{АВ} =P{х,у} =F₂(x,y). ФункцияF₂(x,y) называетсядвумернойинтегральнойфункциейраспределениявероятностей. Очевидно, чтоF₂(x,) =F₁(x),F₂(,y) =F₁(y),F₂(x, –) =F₂(–,y) = 0. Если двумерная функцияF₂(x,y) дважды дифференцируема, можно определить

­–двумернаяплотностьвероятности, или двумернаяфункцияраспределения. Естественно, что

.

Кроме того,

(1.0)

Для независимых случайных величин, естественно, что

F₂(x, y) = F₁(x)F₁(y), ₂(x, y) = ₁(x)₁(y). Для зависимых случайных величини существует условная вероятность того, что одна из них находится ниже уровняy,если другая заключена в пределах от xдоx₁. Из формул(1.2)и (1.12)получаем:

.

Переходя к пределу х₁  х,получим:

.

Функция F₂(y|x) называетсяусловнойинтегральнойфункциейраспределенияслучайной величиныпри условии, что=x. Частная производная от неё поyназываетсяусловнойфункциейраспределенияслучайной величины при условии, что=x:

. (1.0)

Из формул (1.12)и (1.13)можно получитьформулуполнойвероятности:

. (1.0)

Учитывая формулу (1.14),можно, по аналогии с соотношением (1.13),записать:

. (1.0)

Формула (1.15) –аналог формулы Байеса (1.5)для случайной величины.

В общем случае для совокупности из nслучайных величин₁,₂, …,_nможно ввестиn-мерную интегральную функцию распределения

F_n(x₁, …,x_n) =P{₁x₁, …,_nx_n} иn-мерную функцию распределения

.

Для взаимно независимых случайных величин ₁,₂, …,_n, естественно,

.

Заметим, что совокупность nслучайных величин₁,₂, …,_nможно рассматривать как компоненты случайного вектора вn-мерном пространстве. Пусть событиеAзаключается в том, что конец вектора попадает в некоторую областьGn-мерного пространства. Тогда

.

Легко показать аналогично выводу соотношений (1.12)и (1.13),что

, (1.14')

. (1.15')

Для совокупности случайных величин определены моменты

,

центральные моменты

,

и смешанные моменты

,

.

Смешанный центральный момент второго порядка называется ковариацией:

.

Для независимых случайных величин ₁и₂имеемМ₂(₁,₂) = 0. Без­раз­мер­ная величина

называется коэффициентом корреляциислучайных величин₁и₂. Конечно, |R(₁,₂)|1. ЕслиR(₁,₂) = 0,то случайные величины₁и₂называютсяне­кор­релированными. Независимые случайные величины всегда некорре­ли­ро­ван­ны, обратное не обязательно. Еслиm₂(₁,₂) = 0,то случайные величины₁и₂называютсяортогональными.

Вводятся также условные моменты

,

.

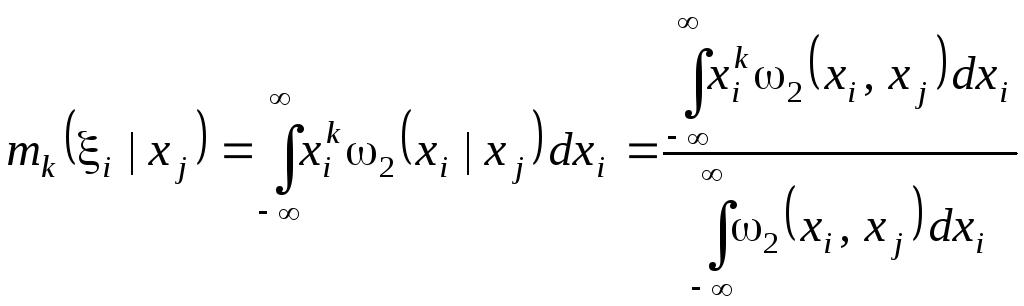В качестве примера можно рассмотреть многомерное нормальное рас­п­ре­де­ление совокупности случайных величин (₁, …,_n) :

, (1.0)

гдеD– главный определитель корреляционной матрицы вида:

,

причем r_{i j}=r_{j i}, |r_{i j}| < 1, аD_{i j}– алгебраическое дополнение элементаr_{i j}. Можно показать, что <_i> =x_i,M₂(_i) =_i²,R(_i,_j) =r_{i j}.

С помощью формулы (1.12 в новых лекциях 1.17)нетрудно убедиться, что каждая случайная величина_iиз совокупности, имеющей совместное нормальное распределение вида (1.16),распределена по нормальному закону вида (1.8 в новых лекциях 1.12).Обратное, вообще говоря, не верно. Частным случаем многомерного нормального распределения (1.16)является двумерное нормальное распределение:

. (1.0)

Разумеется, M₂(₁,₂) =r₁₂,M₂(₂|x₁) =₂²(1 –r²), M₂(₁|x₂) =₁²(1 –r²).

Рассмотрим на плоскости х₁,х₂случайную точку (конец случайного век­то­ра ),координаты которой₁,₂–независимые случайные величины, рас­п­ре­де­лен­ные по двумерному нормальному закону (1.17),причем ₁=₂=,

r= 0,₁=₂= 0. Найдем вероятность того, что точка (₁,₂) лежит внутри круга радиуса:0

,

– (1.0)

релеевскоераспределение.