5.4.Спектр колебаний с флуктуирующей частотой

Рассмотрим узкополосный случайный процесс вида (5.7)

(t) = A₀cos[₀t + (t) + ₀], (5.0)

где (t) =d(t)/dt–девиация мгновенной частоты, стационарный случайный процесс;₀–начальная фаза,случайная величина, равномерно распределённая на интервале [0, 2];А₀ –постоянная амплитуда, её флуктуации отсутствуют. Выбором соответствующего значения центральной частоты₀можно добиться, чтобы <(t)> = 0.Тогда

,

где G_⁺() – спектральная плотность интенсивности случайного процесса(t) по положительным частотам.

Случайный набег фазы за время от tдоt +равен

.

Для его среднего квадрата получаем

(5.0)

Таким образом, средний квадрат набега фазы полностью определён спектральной плотностью интенсивности флуктуаций частоты.

Пусть теперь (t),а значит, и_(t) =_–– нормальный процесс. Поскольку <_(t)> = 0, а дисперсия определена соотношением(5.21),распределение случайной величины_(t) имеет вид (1.8),то есть

.

Усредняя произведение

(t)(t + ) = A₀²{cos[₀ – (_ – )] + cos[₀(2t + ) + (_ + ) + 2₀]}/2

при помощи нормального распределения для и равномерного для₀,получим

B_() = A₀²cos(₀)<cos()>/2 = A₀²e^–D()/2cos(₀)/2.

Тогда спектральная плотность интенсивности процесса (t) по положительным частотам в силу соотношения (4.6)равна

. (5.0)

Здесь мы отбросили интеграл, содержащий быстро осциллирующий множитель cos((+₀)). Если же нужно получить по известному спектру процесса(t), который легко измерить, спектр флуктуаций частоты(t), нужно решать нелинейное интегральное уравнение, подставляя в формулу (5.22)соотношение (5.21).

Рассмотрим только несколько предельных случаев. Соотношения (5.21)и (4.5)позволяют ввести средний квадрат флуктуации частоты

.

Можно также ввести интервал корреляции _процесса(t) так, что. Пусть теперь <²>_²>> 1, то есть частота колебания вида (5.20)испытывает большие и медленные уходы, или <²>_>>1/_. Тогда для<<_~ 1 разложим в соотношении (5.21) под интегралом

1 – cos()²²/2 и получим

.

Подставляя это выражение в формулу (5.22),получаем

.

Здесь существенны только значения ,что и оправдывает разложение. Выполняя интегрирование, получим:

.

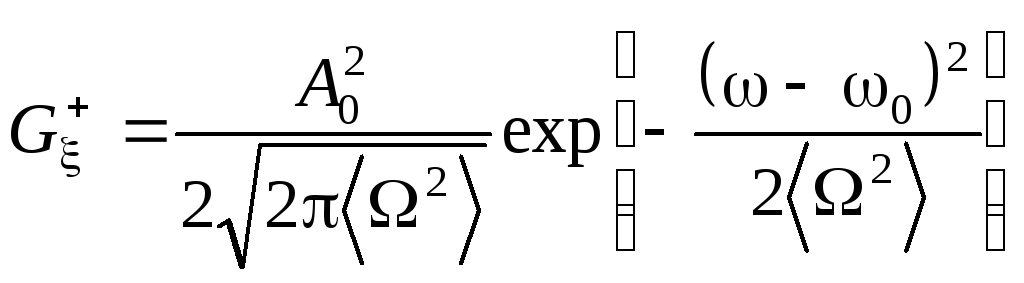Toесть в этом случае получается гауссова (колокольная) форма спектральной линии, характерная, например, для доплеровского уширения спектральных линий.

Рассмотрим второй предельный случай. Пусть <²>_²<< 1, то есть частота колебаний вида(5.20)испытывает малые и быстрые флуктуации, или

<²>_<< 1/_. В этом случае в интеграле (5.21) существенны только значенияG_⁺(), лежащие в пределах главного максимума множителя (1 – cos())/², то есть от= 0 до= 1/.Поэтому, еслиG_⁺(0)0 и>>_, то

(5.0)

Соотношение (5.22)теперь даёт:

.

Здесь существенны только значения < 1/B,это совместимо с предложением>> _,еслиB_=G_⁺(0)_/2 << 1. Для достаточно монотонного убывания функцииG_⁺() можно взять <²>G_⁺(0)/_. Тогда предположение

_<< 1/Bудовлетворено в силу исходного предположения <²>_²<< 1. Выполняя интегрирование, получаем:

,

то есть лоренцеву (резонансную) форму, которую имеют спектральные линии вследствие уширения из-за соударений.