7.4.Двумерные случайные блуждания

Формула (7.15)позволяет судить о динамике излучаемой мощности лазе­ра, но ничего не говорит о статистике амплитуды излучаемых колебаний, то есть не позволяет записать поле излучения в виде(5.7),хотя процесс этот, по-видимому, узкополосный. Здесь более уместна, например, модель, при которой все атомы при переходе излучают одну и ту же частоту, с одной и той же амп­ли­тудой, но случайной фазой, то есть излучение лазера представляет собой случайный процесс

. (7.0)

Воспользовавшись методом комплексной амплитуды, можно записать

,

то есть результирующий вектор является суммой боль­шого числа векторовс одинаковыми модулямиаи случайными фазами_i. Этот случай, очевидно, эквивалентен двумерному броу­новскому движению, когда частица за времясовершает скачок на расстояниеaв случайном направлении_i,то есть задача (7.16)о сложении колебаний со случайными фазами вполне эквивалентна задаче о координатах броу­но­в­с­кой частицы в момент времениt=N.

Рассмотрим случай изотропных блужданий, когда все направления вектора равновероятны, иными словами, распределение фазы_i– равномерное, причем все_i–независимые случайные величины. Попадание частицы в момент времениtв точку с координатами (x,y) может произойти в результате перехода с любой точки окружности радиусаaс центром в точке (x,y), если частица в моментt –  была на этой окружности

.

Предположим теперь, что существует предел

. (7.0)

Тогда в результате предельного перехода при 0 получим

(7.0)

– двумерноеуравнениедиффузии.

Если в начальный момент времени частица находилась в начале координат x=y= 0 (для задачи о колебаниях со случайной фазой это значит, что приN= 0 колебания отсутствуют), то начальным условием для уравнения (7.18)будет:

(0, x, y) = (x)(y).

Решение, нормированное при данных условиях, имеет вид:

, (7.0)

где ²=Bt(ср. 5.23) и является произведением нормальных распределений похиу, которые в следствие этого независимы. В 1-мразделе показано, что модуль вектора, компоненты которого независимы и имеют нормальное распределение с нулевым средним и одинаковыми дисперсиями, имеет релеевское распределение вида (1.18):

.

Для задачи о сложении случайных колебаний, учитывая, что t=N, перепишем условие (7.17)в виде 2B=Na²/t(N>> 1), или²=Bt=Na²/2. Тогда распределение амплитуды суммы большого числа колебаний со случайными фазами примет вид

.

7.5.Уравнение Фоккера – Планка – Колмогорова

Нелинейное интегральное уравнение Смолуховского (7.6)можно свести при определенных допущениях к линейному дифференциальному уравнению в частных производных, что гораздо удобнее. Выберем моменты времени

t₀<t–<tи обозначим(t₀) =x₀,(t–) =y,(t) =x. Предположим, что существуют пределы:

Умножим уравнение Смолуховского (7.6)на произвольную функциюq(x), такую, что. Положив t₂=t–и интегрируя по x,получим

Переходя к пределу при 0 и интегрируя по частям, получим после замены переменных интегрирования:

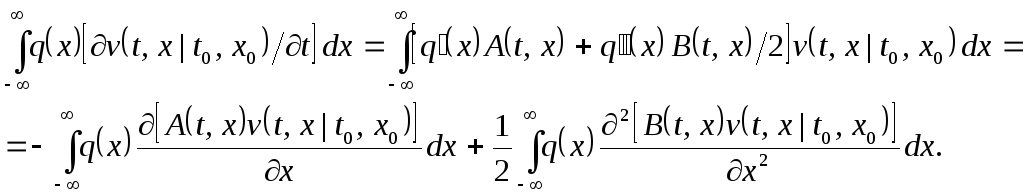
В силу произвольности функции q(x) получаемуравнение Фоккера –Планка –Колмогорова (ФПК) в виде

, (7.0)

называемое иногда вторым уравнением Колмогорова.Начальные условия его

v(t₀,x|t₀,x₀) =(x–x₀).

При этом функция v(t,x|t₀,x₀) должна быть неотрицательна и нормирована к единице. Аналогично, выбрав моменты времениt₀<t₀+<t, можно получитьпервоеуравнениеКолмогорова:

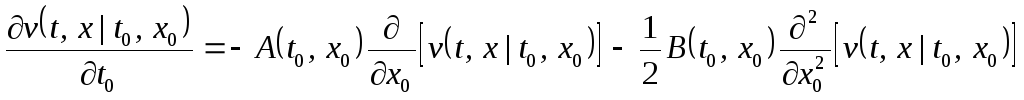. (7.0)

Если нас интересует не динамика вероятностей переходов вида (7.20),а динамика распределения вероятностей, то, воспользовавшись соотношением (7.1)в виде

₂(t, x, t₀, x₀) = (t₀, x₀)v(t, x|t₀, x₀)

и условием согласования (7.4)

,

можно умножить уравнение ФПК (7.20)на начальное распределение(t₀,x₀) и, проинтегрировав поx₀,получить

.(7.0)

Разумеется, решение этого уравнения с начальным условием (t₀,x₀) должно быть неотрицательно и нормировано к единице.

Введем условное среднее

.

Умножая уравнение (7.20)наxи проинтегрировав его пох, получаем

.

Для физически значимых случаев проинтегрированные члены стремятся к нулю при |x|  . В этом случае:

dx/dt = A(t, x). (7.0)

Это –феноменологическое уравнение движения, удовлетворяющее начальному условиюx(t₀) = x₀. Заметим, что для линейной функцииA(t,x) =a(t)x+b(t) уравнение (7.23)имеет классический вид:

dx/dt = a(t)x + b(t).

Уравнение (7.23)описывает изменение среднего значения случайного процесса x, оно меняется только под действием членаA(t,x), который ответственен за детерминированный "снос" и часто так и называется –коэффициент сноса. Соответственно член сВ(t,x) описывает отклонениеx(t) от своего математического ожиданияxи называетсякоэффициентом диффузии.

Для стационарного марковского процесса A(x),В(x) и(x) не зависят от времениt. Тогда из уравнения (7.22)получаем:

.

Отсюда следует, что

, (7.0)

где постоянная Сопределяется из условия нормировки.

Для совокупности nслучайных величин_I(t),i= 1, 2, …, или векторной случайной функциивn-мерном, в общем случае криволинейном, прос­т­ра­н­с­тве, где– значение функции , можно ввести элемент объема. Тог­да для вероятности перехода условие нормировки имеет вид:

.

Уравнение Смолуховского принимает вид:

и соответственно уравнение ФПК записывается в виде

, (7.0)

где

Нетрудно видеть, что уравнение (7.18)для задачи диффузии или сложения случайных колебаний –частный случай многомерного уравнения ФПК (7.25)для двумерных декартовых координат приQ(x,y) = 1,A(t,x,y) = 0,

B(t, x, y) = B = const.