
matan_vse_baza
.pdf
18.12.13 mypage.i-exam.ru/index.php?menu=show_test&login=05ps1845140
Частная производная второго порядка |
функции |
имеет |
вид … |
|
|
Решение:
 При вычислении частной производной функции по одной из
При вычислении частной производной функции по одной из
 переменных другую переменную рассматриваем как постоянную величину.
переменных другую переменную рассматриваем как постоянную величину.
 Тогда
Тогда
и
 ЗАДАНИЕ N 22 отправить сообщение разработчикам
ЗАДАНИЕ N 22 отправить сообщение разработчикам
Тема: Полный дифференциал ФНП
Полный дифференциал функции 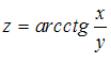 имеет вид …
имеет вид …
mypage.i-exam.ru/index.php?menu=show_test&login=05ps1845140 |
12/15 |

18.12.13 mypage.i-exam.ru/index.php?menu=show_test&login=05ps1845140
Решение:
 Полный дифференциал функции нескольких переменных равен сумме
Полный дифференциал функции нескольких переменных равен сумме
 произведений частных производных этой функции на дифференциалы
произведений частных производных этой функции на дифференциалы
 соответствующих независимых переменных, то есть
соответствующих независимых переменных, то есть
 Тогда
Тогда
 ЗАДАНИЕ N 23 отправить сообщение разработчикам
ЗАДАНИЕ N 23 отправить сообщение разработчикам
Тема: Непосредственное интегрирование
Множество первообразных функции |
имеет вид … |
Решение:
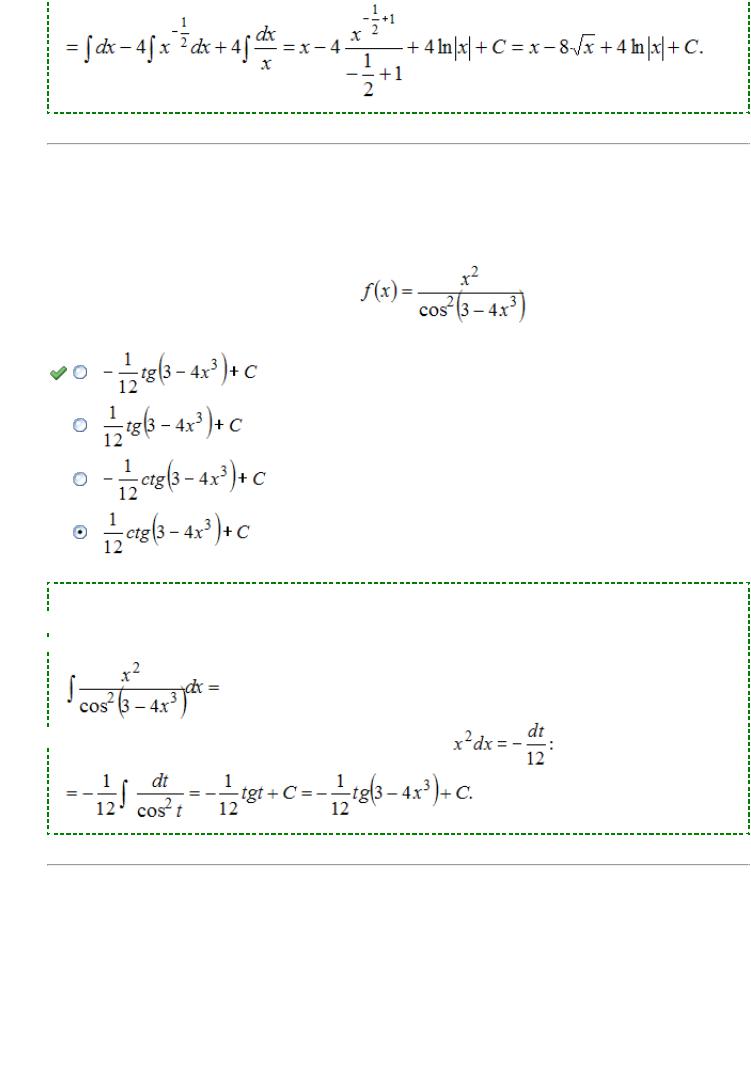
 Чтобы определить множество первообразных, вычислим неопределенный
Чтобы определить множество первообразных, вычислим неопределенный
 интеграл от этой функции. Тогда
интеграл от этой функции. Тогда
mypage.i-exam.ru/index.php?menu=show_test&login=05ps1845140 |
13/15 |
18.12.13 |
mypage.i-exam.ru/index.php?menu=show_test&login=05ps1845140 |
 ЗАДАНИЕ N 24 отправить сообщение разработчикам
ЗАДАНИЕ N 24 отправить сообщение разработчикам
Тема: Замена переменной в неопределенном интеграле
Множество первообразных функции |
имеет вид … |
Решение:
 Чтобы определить множество первообразных, вычислим неопределенный
Чтобы определить множество первообразных, вычислим неопределенный
 интеграл от этой функции. Тогда
интеграл от этой функции. Тогда
 Произведем замену
Произведем замену 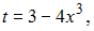
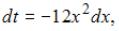
 ЗАДАНИЕ N 25 отправить сообщение разработчикам
ЗАДАНИЕ N 25 отправить сообщение разработчикам
Тема: Интегрирование по частям в неопределенном интеграле
Множество первообразных функции 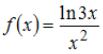 имеет вид …
имеет вид …
mypage.i-exam.ru/index.php?menu=show_test&login=05ps1845140 |
14/15 |

18.12.13 |
mypage.i-exam.ru/index.php?menu=show_test&login=05ps1845140 |
|
|
|
|
|
|
|
Решение:
 Чтобы определить множество первообразных, вычислим неопределенный
Чтобы определить множество первообразных, вычислим неопределенный
 интеграл от этой функции методом интегрирования по частям по формуле
интеграл от этой функции методом интегрирования по частям по формуле  Тогда
Тогда
mypage.i-exam.ru/index.php?menu=show_test&login=05ps1845140 |
15/15 |

18.12.13 |
mypage.i-exam.ru/index.php?menu=show_test&login=05ps1845117 |
Преподаватель: Филиппов С.Д. Специальность: 080200.62 - Менеджмент Группа: Мт-153 Дисциплина: Математика
Идентификатор студента: Койков Сергей Андреевич
Логин: 05ps1845117
Начало тестирования: 2013-12-15 11:21:47 Завершение тестирования: 2013-12-15 12:08:38 Продолжительность тестирования: 46 мин. Заданий в тесте: 25 Кол-во правильно выполненных заданий: 11
Процент правильно выполненных заданий: 44 %
 ЗАДАНИЕ N 1 отправить сообщение разработчикам
ЗАДАНИЕ N 1 отправить сообщение разработчикам
Тема: Вычисление определителей
Определитель не равный нулю может иметь вид …
Решение:
 Вычислим каждый из определителей, например, разложением по первой строке:
Вычислим каждый из определителей, например, разложением по первой строке: 
 1)
1)
mypage.i-exam.ru/index.php?menu=show_test&login=05ps1845117 |
1/15 |

18.12.13 |
mypage.i-exam.ru/index.php?menu=show_test&login=05ps1845117 |
 2)
2)
 3)
3)
 4)
4)
 ЗАДАНИЕ N 2 отправить сообщение разработчикам
ЗАДАНИЕ N 2 отправить сообщение разработчикам
Тема: Линейные операции над матрицами
Даны матрицы |
и |
Тогда решением уравнения |
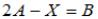 является матрица X, равная …
является матрица X, равная …
 ЗАДАНИЕ N 3 отправить сообщение разработчикам
ЗАДАНИЕ N 3 отправить сообщение разработчикам
Тема: Умножение матриц
mypage.i-exam.ru/index.php?menu=show_test&login=05ps1845117 |
2/15 |

18.12.13 mypage.i-exam.ru/index.php?menu=show_test&login=05ps1845117
Даны матрицы и Тогда существует
произведение матриц …
 ЗАДАНИЕ N 4 отправить сообщение разработчикам
ЗАДАНИЕ N 4 отправить сообщение разработчикам
Тема: Ранг матрицы
Ранг матрицы |
равен двум, если значение x равно … |

 2
2
 0
0
 – 2
– 2  1
1
Решение:
 Рангом матрицы называется наибольший из порядков ее миноров, не равных
Рангом матрицы называется наибольший из порядков ее миноров, не равных
 нулю. Так как существуют ненулевые миноры второго порядка, например:
нулю. Так как существуют ненулевые миноры второго порядка, например:  то ранг матрицы A будет равен двум,
то ранг матрицы A будет равен двум,
 если минор третьего порядка равен нулю. Вычислим
если минор третьего порядка равен нулю. Вычислим
 Следовательно,
Следовательно, 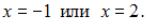
 ЗАДАНИЕ N 5 отправить сообщение разработчикам
ЗАДАНИЕ N 5 отправить сообщение разработчикам
Тема: Обратная матрица
mypage.i-exam.ru/index.php?menu=show_test&login=05ps1845117 |
3/15 |

18.12.13 |
mypage.i-exam.ru/index.php?menu=show_test&login=05ps1845117 |
Для матрицы |
не существует обратной, если a равно … |
Решение:
 Матрица не имеет обратной, если определитель матрицы равен нулю, то есть
Матрица не имеет обратной, если определитель матрицы равен нулю, то есть  тогда
тогда
 обратной матрицы не существует при
обратной матрицы не существует при 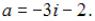
 ЗАДАНИЕ N 6 отправить сообщение разработчикам
ЗАДАНИЕ N 6 отправить сообщение разработчикам
Тема: Системы линейных уравнений
Единственное решение имеет однородная система линейных уравнений …
mypage.i-exam.ru/index.php?menu=show_test&login=05ps1845117 |
4/15 |

18.12.13 |
mypage.i-exam.ru/index.php?menu=show_test&login=05ps1845117 |
 ЗАДАНИЕ N 7 отправить сообщение разработчикам
ЗАДАНИЕ N 7 отправить сообщение разработчикам
Тема: Прямоугольные координаты на плоскости
Расстояние от точки 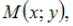 лежащей на оси ординат, до точки
лежащей на оси ординат, до точки 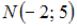 равно 2. Тогда точка
равно 2. Тогда точка 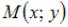 имеет координаты …
имеет координаты …
Решение:
Так как точка |
лежит на оси ординат, то ее абсцисса |
Тогда |
||
расстояние между точками |
и |
можно определить как |
||
|
|
или |
Тогда |
|
 ЗАДАНИЕ N 8 отправить сообщение разработчикам
ЗАДАНИЕ N 8 отправить сообщение разработчикам
Тема: Прямая на плоскости
Уравнение прямой, проходящей через точку пересечения прямых 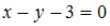 и
и 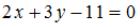 перпендикулярно прямой
перпендикулярно прямой 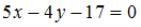 имеет вид …
имеет вид …
Решение:
Уравнение прямой, перпендикулярной прямой |
|
можно |
|
определить как |
, где для определения |
найдем точку |
|
пересечения прямых |
и |
: |
|
mypage.i-exam.ru/index.php?menu=show_test&login=05ps1845117 |
5/15 |

18.12.13 |
mypage.i-exam.ru/index.php?menu=show_test&login=05ps1845117 |
Подставим в уравнение прямой |
координаты точки |
: |
|
|
, отсюда |
Тогда уравнение искомой прямой примет |
|
вид |
. |
|
|
 ЗАДАНИЕ N 9 отправить сообщение разработчикам
ЗАДАНИЕ N 9 отправить сообщение разработчикам
Тема: Кривые второго порядка
Центр окружности 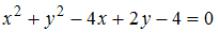 имеет координаты …
имеет координаты …
 ЗАДАНИЕ N 10 отправить сообщение разработчикам
ЗАДАНИЕ N 10 отправить сообщение разработчикам
Тема: Плоскость в пространстве
Уравнение плоскости, проходящей через точки 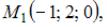
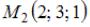 и
и 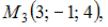 имеет вид …
имеет вид …
 ЗАДАНИЕ N 11 отправить сообщение разработчикам
ЗАДАНИЕ N 11 отправить сообщение разработчикам
Тема: Прямая линия в пространстве
mypage.i-exam.ru/index.php?menu=show_test&login=05ps1845117 |
6/15 |
