4.3.Плотность распределения

Пусть имеется непрерывная случайная величина Хс функцией распределенияF(x), которую мы предположим непрерывной и дифференцируемой. Вычислим вероятность её попадания на участок отхдох+х:

Уменьшая х,в пределе получим производную.

Введём обозначение- производная функции распределения характеризует плотность, с которой распределены значения случайной величины в данной точке. Она называетсяплотностью распределения(плотностью вероятности) непрерывной случайной величины. Кривая, изображающая плотность, называется кривой распределения.

Рассмотрим непрерывную случайную величину Хс плотностью распределенияf(x)и элементарный участокdx, примыкающий к точке х. Вероятность попадания случайной величины в участок отхдоx+dxравнаf(x)dx.

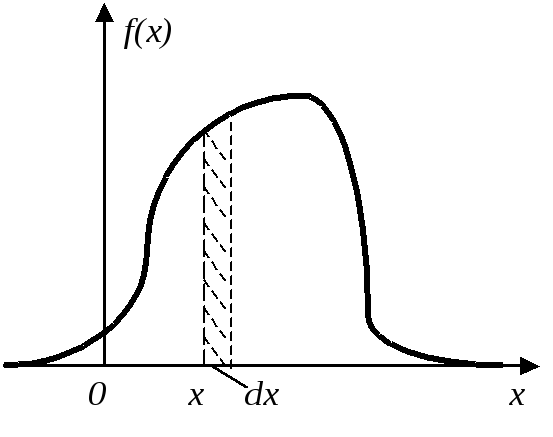
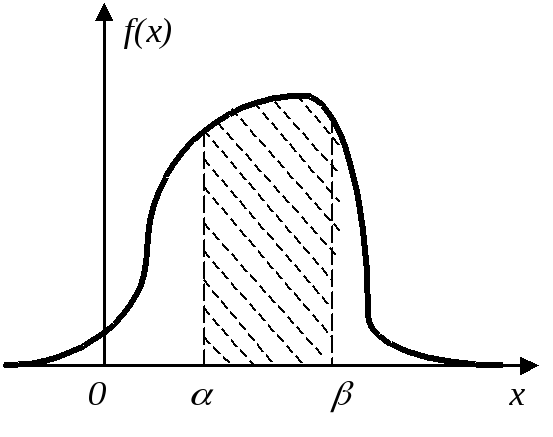
Рис.4.3.1.Графики плотности распределения непрерывной случайной

величины случайной.

Выразим вероятность попадания величины Х на отрезок от до.

(4.3.1)

Геометрически это есть площадь под кривой распределения.

Выразим функцию распределения через плотность.

(4.3.2)

Геометрически F(x)есть площадь кривой распределения левее точких.

Основные свойства плотности распределения.

1. Плотность распределения есть положительная функция.

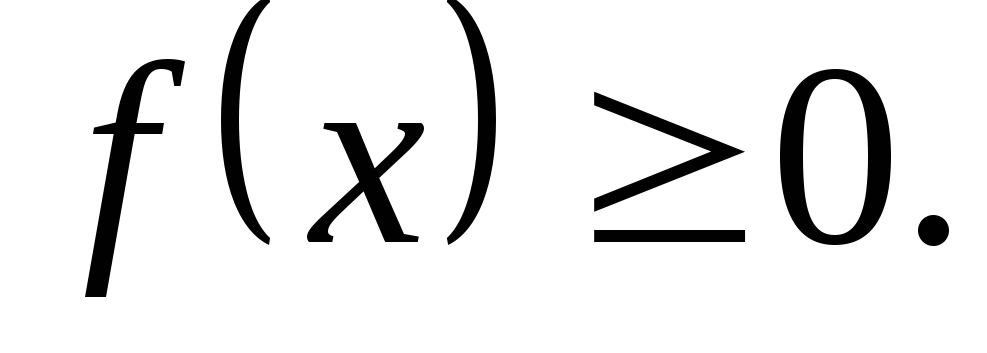
2. Интеграл в бесконечных пределах от плотности распределения =1:

(4.3.3)

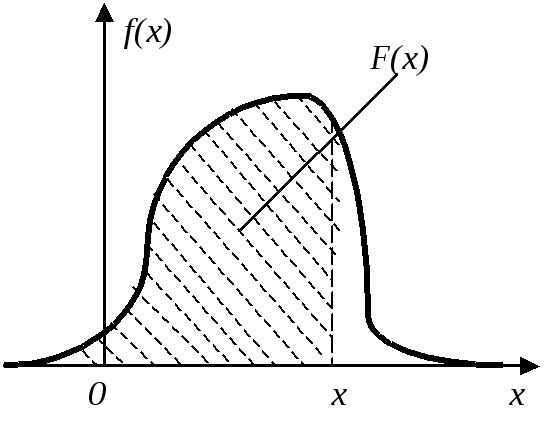
Рис.4.3.2.Иллюстрация к формуле (4.3.2)

Пример. Случайная величинаХподчинена закону распределения с плотностью:

при (4.3.4)

при

Найти коэффициент а,построить график плотности распределенияf(x). Найти функцию распределенияF(x)и построить её график. Найти вероятность попадания величиныХна участок от 0 до

Решение. График плотностиf(x):

Рис.4.3.3.График плотности распределения (4.3.4).

По свойству плотности распределения

Функция распределения:

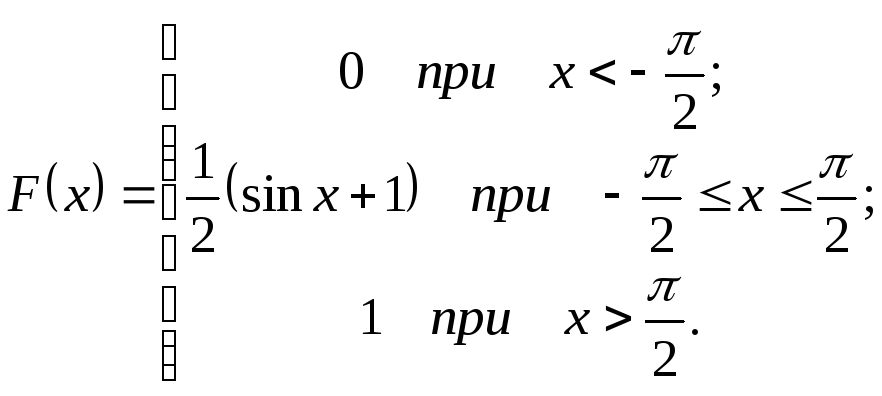(4.3.5)

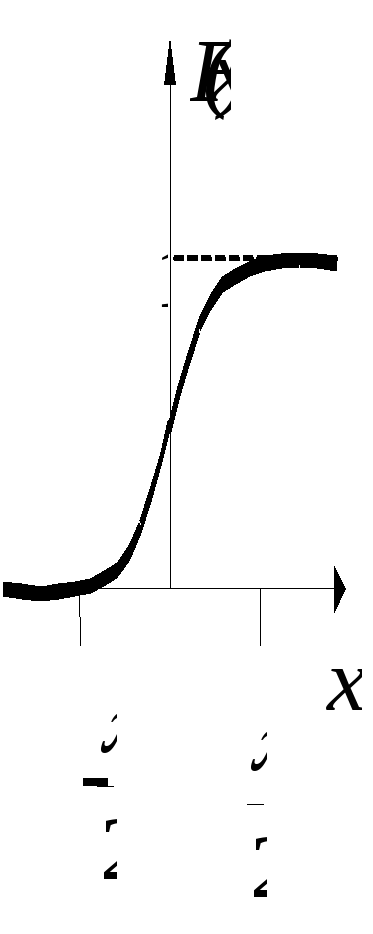
Рис.4.3.4.График функции распределения (4.3.5)

Вероятность попадания в интервал от 0 до

5.Числовые характеристики случайных величин

5.1.Характеристики положения

Закон распределения случайной величины является ее исчерпывающей характеристикой. Однако на практике часто не требуется такого полного описания и достаточно знать только некоторые числовые характеристики случайной величины, такие, например, как показатели положения и разброса случайной величины.

Среди числовых характеристик положения случайной величины наиболее важной является математическое ожидание, которое характеризует центр рассеивания случайной величины.

Математическим ожиданиемназывается сумма произведений всех возможных значений случайной величины на вероятности этих значений. С точки зрения механики её можно интерпретировать, как координату центра тяжести вероятностных масс. Если дискретная случайная величинаХ может принимать значенияс вероятностями, то математическое ожиданиеX

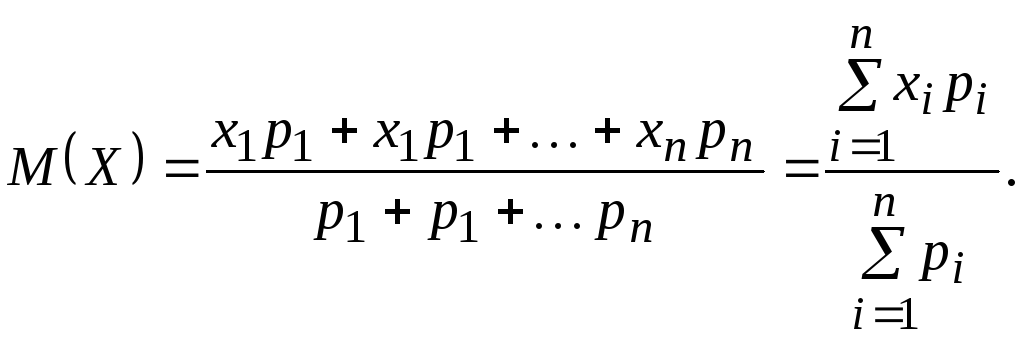
Учитывая, что получим, что

(5.1.1)

Если случайная величина непрерывна, то отмеченная сумма превращается в интеграл

, (5.1.2)

где плотность распределения случайной величиныX.

Рассмотрим среднее арифметическое наблюдённых значений величины Х:

Но есть не что иное, как частота (или статистическая вероятность) события Х. При увеличении числа опытов. Т.е. среднее арифметическое стремится к математическому ожиданию.

Для непрерывных величин:

.

Модойслучайной величины называется её наиболее вероятное значение.

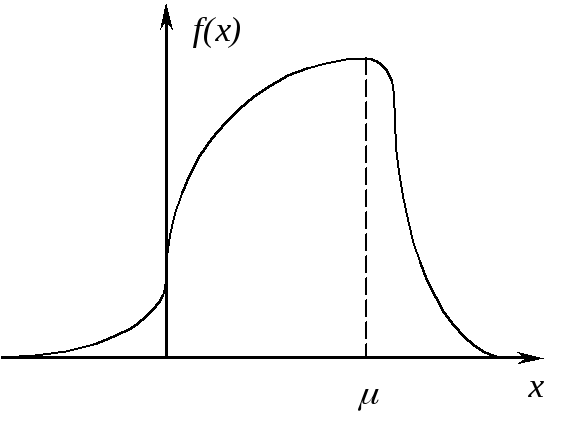
Рис.5.1.1.Иллюстрация к определению моды случайной величины.

Для симметричного распределения мода и математическое ожидание совпадают.

Медианойслучайной величиныХназывается такое её значениеe, для которого

т.е. одинаково вероятно, окажется ли случайная величина меньше или больше e.

Геометрически это абсцисса точки, в которой площадь под кривой распределения делится пополам.

Рис.5.1.2.Иллюстрация к определению медианы.

Так же как в механике для описания распределения масс используются статические моменты и моменты инерции, в теории вероятности используются начальные и центральные моменты.