10.Системы случайных величин

10.1.Понятие о системе случайных величин

На практике распространены ситуации, когда случайное явление характеризуется несколькими случайными величинами. Например, надежность режущего инструмента характеризуют стойкостью T в минутах времени резания и временем восстановления T_в в мин. Габаритные размеры произвольной детали, обрабатываемой на токарном станке характеризуются длиной L и диаметром D. Габаритные размеры корпусной детали характеризуются тремя размерами: длиной L, шириной B , высотой H. Сила резания характеризуется тремя составляющими , то есть проекциями силы резания на соответствующие оси координат станка.

В общем случае систему случайных величин можно рассматривать как многомерную случайную величину, каждое возможное ее значение представляется в виде точки в пространстве с соответствующем числом измерений, координаты которой и есть соответствующие случайные величины. Рассмотрим подробнее двумерный случай.

10.2.Двумерные случайные величины и их законы распределения

Предположим, что (X,Y) – это система двух случайных величин или коротко – двумерная случайная величина. Функцией распределения такой случайной величины называется вероятность выполнения двух неравенств и, то есть

.

Если пользоваться геометрической интерпретацией двумерной случайной величины, то - это вероятность попадания случайной величины(X,Y) в бесконечный квадрант с вершиной в точке (x,y), находящийся левее и ниже ее (см. рис.10.2.1).

Рис.10.2.1.

Функция распределения F(x,y) есть неубывающая функция по x и по y, то есть

При x и y равных бесконечности

. (10.2.1)

Если один из аргументов равен , то

, (10.2.2)

где - функции распределенияX и Y.

Если и, то

. (10.2.3)

Если и, то вероятность этого события

.(10.2.4)

Это правило иллюстрируется рисунком 10.2.2.

Рис.10.2.2. К выводу формулы (10.2.4).

10.3.Плотность распределения двумерной случайной величины

Если распределение F(x,y) непрерывно и дифференцируемо по x и y, то можно ввести аналогично одномерному случаю плотность распределения

. (10.3.1)

Плотностью эта величина называется потому, что

есть вероятность того что X попадет в интервал , аY попадет в интервал , то есть точка(x,y) попадет в прямоугольник размером .

Вероятность попадания в прямоугольную область (см. рис.10.2.2) через плотность выражается так:

. (10.3.2)

Вероятность попадания в произвольную область S определяется как интеграл по области

.

Функция распределения выражается через плотность следующим образом:

. (10.3.3)

Условие нормировки вероятностей:

. (10.3.4)

Безусловные распределения X и Y

. (10.3.5)

Безусловные плотности распределения X и Y

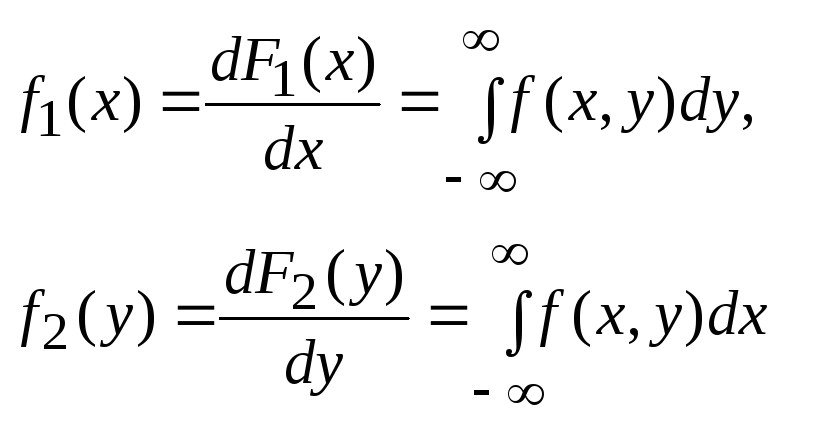. (10.3.6)

10.4. Условные законы распределения

Предыдущие формулы позволили через закон распределения двумерной случайной величины определить распределение каждой из компонент. Можно ли решить обратную задачу, то есть по законам распределения отдельных компонент построить закон распределения двумерной случайной величины? Оказывается, что для этого нужна еще дополнительная информация, а именно, информация о зависимости или независимости компонент между собой. Для этого вводятся так называемые условные законы распределения иили условные плотности.- это вероятность того, чтоX<x при условии, чтоY=y, то есть

,

а

.

Аналогично определяются и.

Между одномерными плотностями и двумерной плотностьюсуществуют следующие связи:

,(10.4.1)

являющиеся следствием закона умножения вероятностей. Отсюда получаем, что

, (10.4.2)

. (10.4.3)