13.2.Распределение суммы случайных величин

Рассмотрим случай, когда третья случайная величина Z является суммой двух независимых случайных величин X и Y, то есть

.

Плотности этих величин соответственно. Плотность распределенияZ

. (13.2.1)

Этот интеграл называется сверткой или композицией плотностей и обозначается следующим образом:

.

Таким образом, если независимые случайные величины суммируются, то их плотности распределения свертываются.

Это правило распространяется на сумму любого числа независимых слагаемых. То есть, если

,

то

.

Пример. Определим плотность распределения суммы двух равномерно распределенных величин X₁ и X₂ c плотностями:

После подстановки этих плотностей в (13.2.1) и интегрирования в предположении получаем , что

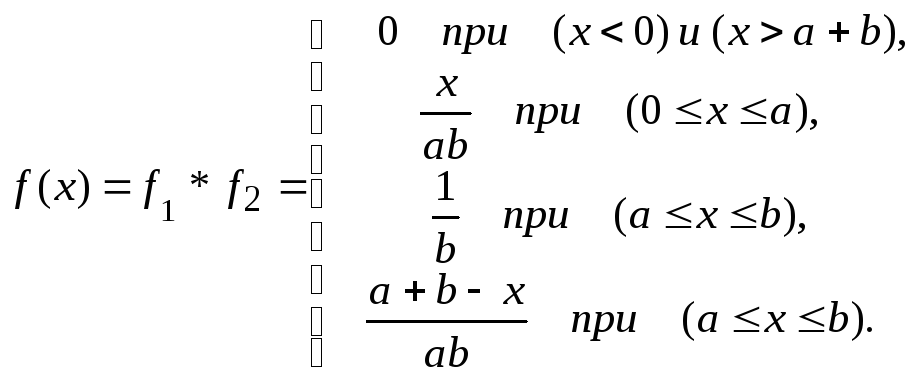
Эта плотность называется трапециодальной (см. рис.13.2.1). Если , то трапеции вырождается в равнобедренный треугольник и соответствующая плотность называется плотностью Сипсона.

Рис.13.2.1.Трапециодальное распределение – свертка двух равномерных распределений.

13.3.Распределение суммы нормально распределенных случайных величин

Если , X и Y независимы и нормально распределены с плотностями

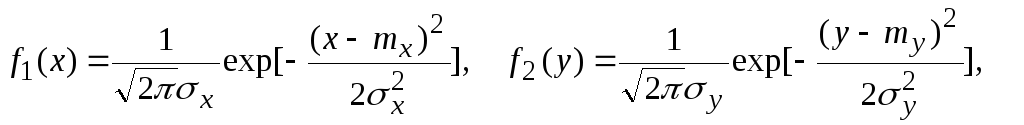то сумма Z будет распределена тоже нормально с плотностью

,

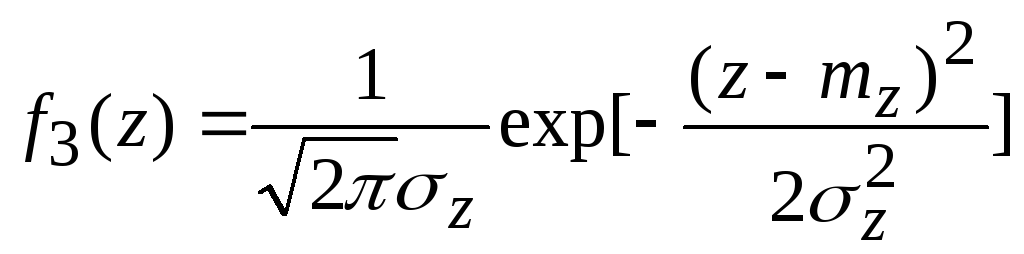где

.

Этот факт доказывается непосредственным интегрированием интеграла сверстки (13.2.1) после подстановки и.

Справедливо и более общее утверждение: если

, (13.3.1)

где иb- константы, а Х_i – независимые нормально распределенные случайные величины со средними значениями и дисперсиями, тоY будет распределено тоже нормально со средним значением

(13.3.2)

и дисперсией

. (13.3.3)

Отсюда вытекает, что если суммируются независимые нормально распределенные случайные величины, то сумма будет иметь тоже нормальное распределение с математическим ожиданием, равным сумме математических ожиданий слагаемых и дисперсией, равной сумме дисперсий слагаемых. То есть, если

,

то

. (13.3.4)

14.Предельные теоремы

14.1.Понятие о законе больших чисел

Из опыта известно, что в массовых явлениях результат мало зависит от отдельных проявлений. Например, давление, оказываемое газом на стенки сосуда, складывается в результате ударов молекул газа о стенки. Не смотря на то, что каждый удар по силе и направлению совершенно случайны итоговое давление оказывается практически детерминированным. То же самое можно сказать о температуре тела, которая определяет среднюю кинетическую энергию движения атомов тела. Сила тока есть проявление движения элементарных зарядов(электронов). Конкретные особенности каждого случайного явления почти не сказываются на среднем результате массы таких явлений. Случайные отклонения от среднего, неизбежные в каждом отдельном явлении, в массе взаимно погашаются, нивелируются, выравниваются. Именно этот факт – устойчивость средних - лежит в основе закона больших чисел: при большом числе случайных явлений средний их результат практически перестает быть случайным и может быть предсказан с большой степенью определенности.

В теории вероятностей под законом больших чисел понимается ряд математических теорем, в каждой из которых при тех или иных условиях устанавливается факт приближения средних характеристик большого числа опытов к постоянным величинам или к предельным распределениям.