10.5.Зависимость и независимость случайных величин

Случайные величины X и Y считаются независимыми, если плотность их совместного распределения равна произведению безусловных плотностей, то есть

. (10.5.1)

Из соотношений (10.4.1) вытекает, что если случайные величины X и Y независимы, то

и .

Пример. Совместная плотность распределения системы случайных величин X и Y имеет вид

.

Определим, зависимы или независимы случайные величины X и Y.

Знаменатель предыдущей плотности разлагается на два множителя, то есть равен

.

Значит

.

Пользуясь формулой (10.3.6), получаем, что

.

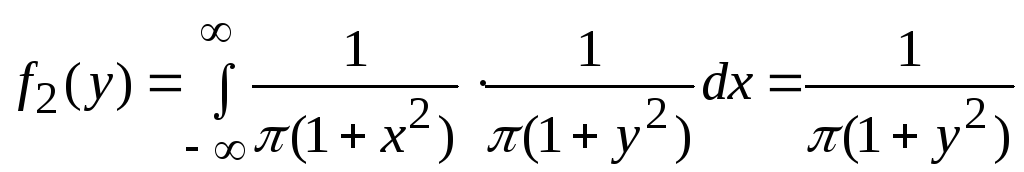
Таким образом

(x),

Следовательно X и Y независимы.

Понятие зависимости случайных величин отличается от функциональной зависимости, когда каждому значению X отвечает только определенное значение Y. Зависимость случайных величин (стохастическая зависимость) предполагает, что конкретному значению X=x отвечает целый спектр возможных значений Y, который описывается законом распределения F(y|x) или плотностью f(x|y). Таким образом, стохастическая зависимость – это менее тесная зависимость, которая превращается в независимость, если . То есть распределениеХ не зависит от значения Y.

Примером стохастической зависимости является зависимость между ростом и весом человека. На практике часто пользуются формулой

.

Эта формула не является точной, а характеризует только в среднем приближенно связь между ростом и весом. Для конкретного человека возможно отклонение в одну и другую сторону. Наиболее полно мы отразим эту зависимость, если определим условную плотность распределения f(y|x) , то есть для каждого значения роста x определим распределение Y.

10.6.Числовые характеристики двумерных случайных величин

Для двумерных случайных величин могут быть определены моменты как и для одномерных.

Начальным моментом порядка (k,s) двумерной случайной величины (X,Y) называется математическое ожидание произведения X^k на Y^s:

. (10.6.1)

Центральным моментом порядка (k,s) двумерной случайной величины (X,Y) называется математическое ожидание произведения на , где

,

то есть

. (10.6.1)

m_X , m_Y – безусловные математические ожидания случайных величин X и Y, то есть

.

На практике обычно используют только моменты первого и второго моментов. Можно показать, что

.

Для дисперсий имеют место следующие соотношения:

Особую роль для двумерных случайных величин играет смешанный центральный момент

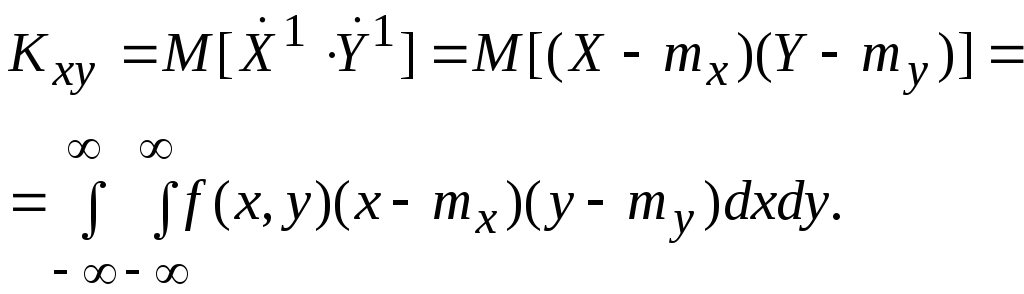(10.6.2)

Этот момент называется корреляционным, так как он характеризует степень зависимости между X и Y. Действительно, если случайные величины независимы, то корреляционный момент равен 0. Покажем это. Если X и Y независимы, то и интеграл (10.6.2) равен в этом случае нулю.

Для характеристики степени зависимости случайных величин чаще применяют безразмерную величину – коэффициент корреляции

, 10.6.3)

- квадратичные отклонения X и Y соответственно. Если X и Y независимы, то и, следовательно,. Обратное утверждение неверно, то есть можно показать, что зависимые величины имеют корреляционный момент и коэффициент корреляции равными нулю. Например, двумерная случайная величина с плотностью

имеет корреляционный момент равный нулю, но X и Y зависимы.

Коэффициент корреляции характеризует тесноту линейной зависимости случайных величин. Если случайные величины X и Y связаны точной линейной зависимостью

то коэффициент корреляции , еслиa>0 и , еслиа<0.

В общем случае, если X и Y связаны стохастически, то

в зависимости от тесноты этой зависимости. Если , то говорят, что междуX и Y имеется положительная корреляция. Если , то говорят, что междуX и Y имеется отрицательная корреляция. Если , то говорят, чтоX и Y не коррелированны. Если X и Y стохастически связаны линейно, отсутствие корреляции равносильно независимости X и Y.