7.3.Числовые характеристики распределения

Аналогом математического ожидания в статистике является среднее арифметическое наблюдённых значений случайной величины или статистическое среднее:

где n– число опытов. Согласно закону больших чисел при неограниченном увеличении числа опытов статистическое среднее приближается к математическому ожиданию. Подобные аналогии существуют для всех числовых характеристик. Будем обозначать их теми же буквами со звёздочкой.

Статистическая дисперсия:

- статистическое среднее.

Аналогично определяются статистические начальные и центральные моменты любых порядков:

Нетрудно доказать, что для статистических моментов справедливы те же свойства, что и для математических моментов. Например, статистический первый центральный момент всегда равен нулю:

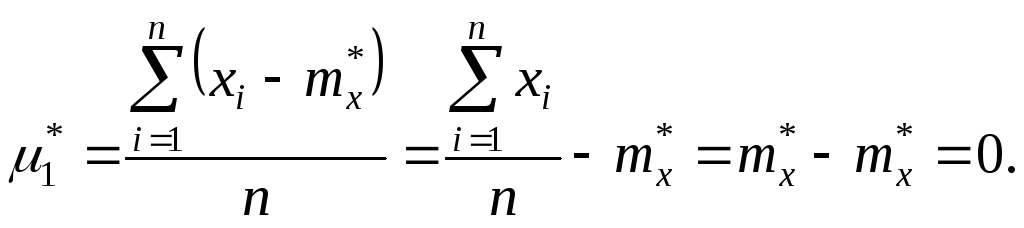
Соотношения между начальными и центральными моментами также сохраняются:

Если число опытов слишком велико и приходится разбивать их на разряды, то получим приближённые формулы:

где - представительi-го разряда,- частотаi-го разряда,k – число разрядов.

7.4.Оценка параметров распределения

При обработке статистического материала часто приходится решать вопрос о том, как подобрать для данного статистического ряда теоретическую кривую распределения. Такая задача называется задачей выравнивания статистических рядов и состоит в подборе теоретической плавной кривой распределения, наилучшим образом описывающей данное распределение.

Наиболее часто применяется метод наименьших квадратов, при котором сумма квадратов отклонений обращается в минимум. Часто вид случайной функции известен заранее, и нужно лишь определить параметры этой функции. Для решения этой задачи часто применяют различные методы оценки параметров.

Чаще всего используют следующие методы:

• метод моментов;

• метод максимального правдоподобия;

• метод минимума хи-квадрата.

7.4.1. Метод моментов.

Согласно методу моментов параметры распределения выбираются таким образом, чтобы моменты статистического распределения совпадали с соответствующими моментами предполагаемого закона распределения. Если предполагаемый закон распределения случайной величины Xимеет один параметр, то он оценивается в результате решения уравнения

.

Если число параметров 2, то приравниваются первые два момента, в результате получаем систему из следующих двух уравнений для оценки неизвестных параметров распределения:

,

.

Если параметров 3, то приравниваются первые три момента и решают систему уже из трех уравнений и так далее.

Проиллюстрируем применения этого метода на конкретных примерах.

Пример 1. В результате наблюдений за работой станка были получены следующие значения наработки до отказа:. Известно, что наработка на отказ подчиняется показательному распределению с плотностью

. (7.4.1)

Для этого распределения , а.

Таким образом, получаем следующую формулу для оценки параметра aпоказательного распределения по опытным данным:

. (7.4.2)

Пример 2. В результате контроля размераXпартии изNдеталей были получены значения. Требуется оценить по этой выборке параметры распределения, в предположении его нормальности. Плотность нормального распределения имеет вид:

. (7.4.3)

Это распределение имеет два параметра и, поэтому для их оценки имеем два уравнения, полученные отмеченным выше приравниванием математических ожиданий и дисперсий:

(7.4.4)

. (7.4.5)

Пример 3. Оценим параметры равномерного распределения случайной величиныXпо выборке.

Плотность равномерного распределения задается следующим образом:

(7.4.6)

В этом случае для оценки параметров aиbметод моментов дает следующие два уравнения:

,

.

В результате решения этой системы получаем:

(7.4.7)

Пример 4. Случайная величинаTимеет гамма распределение с плотностью

, (7.4.8)

где - параметры, подлежащие оценке. Если- реализаци случайной величиныT, то учитывая, что

,

,

получаем:

, (7.4.9)

где

. (7.4.10)

Пример 5. Оценим параметры логарифмически нормального распределения случайной величиныTпо выборке.Плотность распределения

(7.4.11)

Математическое ожидание и дисперсия выражаются через параметры a и следующим образом.

,

Приравнивая теоретические и статистические моменты и решая соответствующие уравнения, получаем:

, (7.4.12)

. (7.4.12)

Пример 6. Дано статистическое распределение боковой ошибки наводки Х при стрельбе с самолёта по наземной цели. Требуется выровнять это распределение с помощью нормального закона.

Инт.	-4; -3	-3; -2	-2; -1	-1;0	0;1	1;2	2;3	3;4
Ni	6	25	72	133	120	88	46	10
pi*	0,012	0,050	0,144	0,266	0,240	0,176	0,092	0,020

Нормальный закон распределения:

Решение. Нормальный закон зависит от двух параметров: m и . Вычислим статистическое среднее:

Для вычисления дисперсии определим второй начальный момент (S=2,k=8).

Задаём параметры нормального закона:

С учётом сглаживания получим вид закона распределения:

Можно построить гистограмму и сглаженный график.

Пример 7. С целью исследования закона распределения ошибки измерения дальности с помощью радиодальномера произведено 400 измерений дальности. Результаты опытов представлены в виде статистического ряда. Выровнять статистический ряд с помощью закона равномерной плотности.

Решение. Закон равномерной плотности выражается формулой

и зависит от двух параметров и.

Математическое ожидание и дисперсия для закона равномерной плотности:

Инт.,м	20;30	30;40	40;50	50;60	60;70	70;80	80;90	90;100
mi	21	72	66	38	51	56	64	32
pi*	0,052	0,180	0,165	0,095	0,128	0,140	0,160	0,080

Перенесём начало отсчёта в точку х₀=60. Получим таблицу

xi	-35	-25	-15	-5	5	15	25	35
pi*	0,052	0,180	0,165	0,095	0,128	0,140	0,160	0,080

где x – среднее для разряда значение ошибки дальномера.

Статистическое среднее приближённо равно

Второй статистический момент равен

Статистическая дисперсия:

Возвращаемся в прежнее начало

Дисперсия та же.

Параметры закона равномерного распределения определим из решения системы уравнений.

Решение: .

Плотность распределения

Гистограмма и плотность равномерного распределения показаны на рисунке.