5.3.Закон равномерной плотности

В некоторых задачах встречаются непрерывные случайные величины, все возможные значения которых лежат в пределах определённого интервала и равновероятны. Говорят, что они распределяются по закону равномерной плотности. Примеры: рулетка, угол поворота сбалансированного колеса и т. д.

Рассмотрим случайную величину, подчинённую закону равномерной плотности на участке от до.

Рис.5.3.1.График равномерной плотности

Плотность распределения f(x)постоянна и равнаСна участке отдо. Вне этого отрезка она равна 0.

Так как площадь под кривой распределения равна 1:

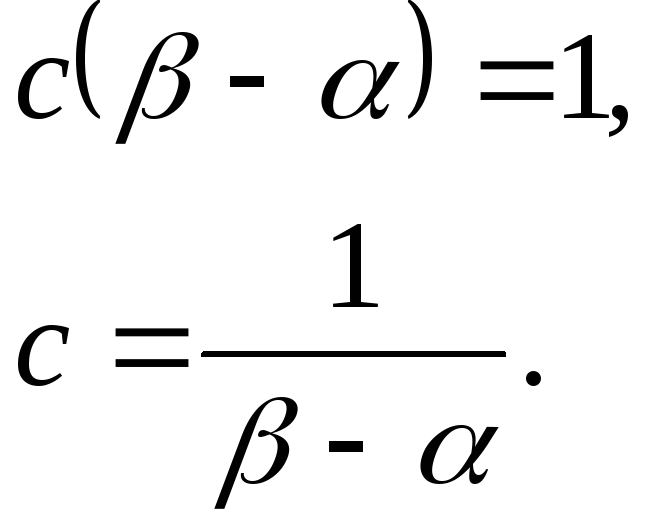
Функция распределения:

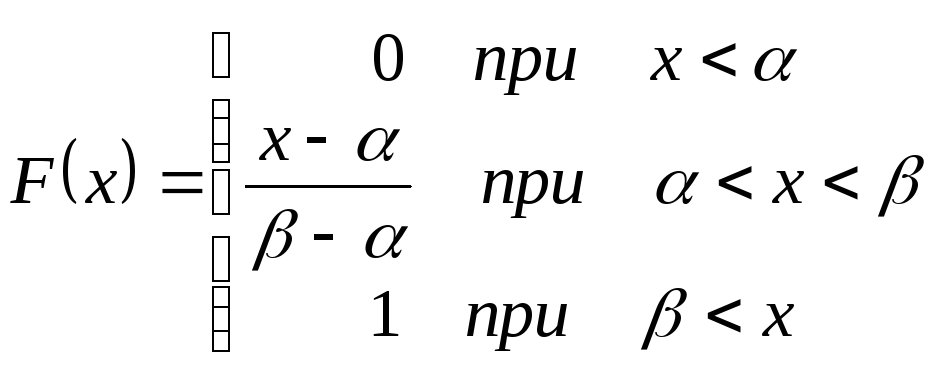
Рис.5.3.2. График равномерного распределения.

Определим основные числовые характеристики случайной величины с равномерным распределением на участке от до.

Математическое ожидание:

В силу симметричности распределения медиана также равна Моды у закона равномерной плотности нет.

Дисперсия:

Среднее квадратичное отклонение:

Асимметрия у симметричного распределения равна нулю.

Для определения эксцесса находим четвёртый центральный момент:

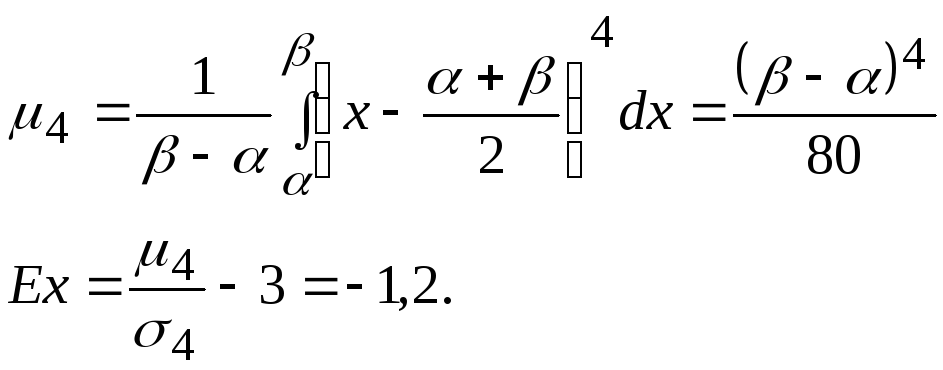
Среднее арифметическое отклонение:

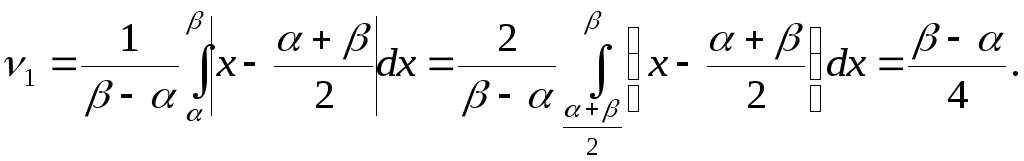
Найдём вероятность попадания случайной величины Хв участок[a,b].

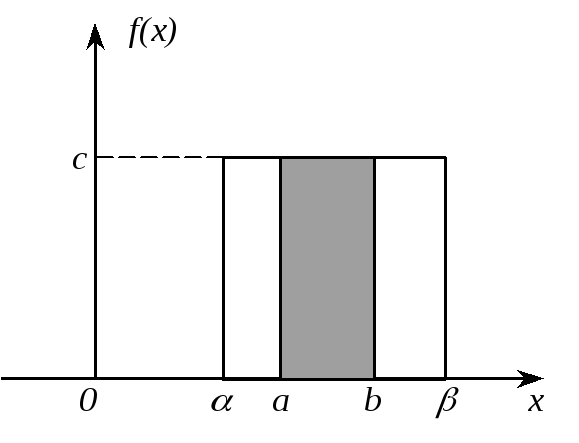
Рис.5.3.3. К определению вероятности .

5.4.Распределение Симпсона

Плотность этого распределения имеет вид равнобедренного треугольника (см.рис.5.4.1).

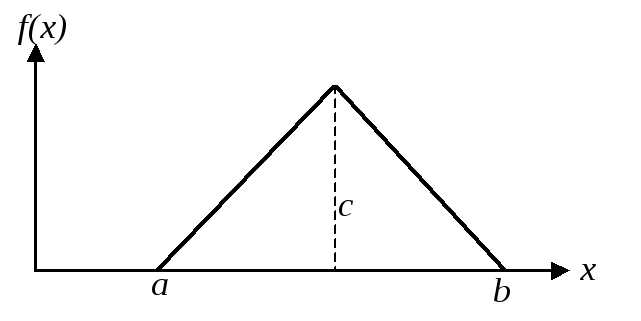
Рис.5.4.1. График плотности Симсона.

Аналитическое выражение для плотности имеет вид:

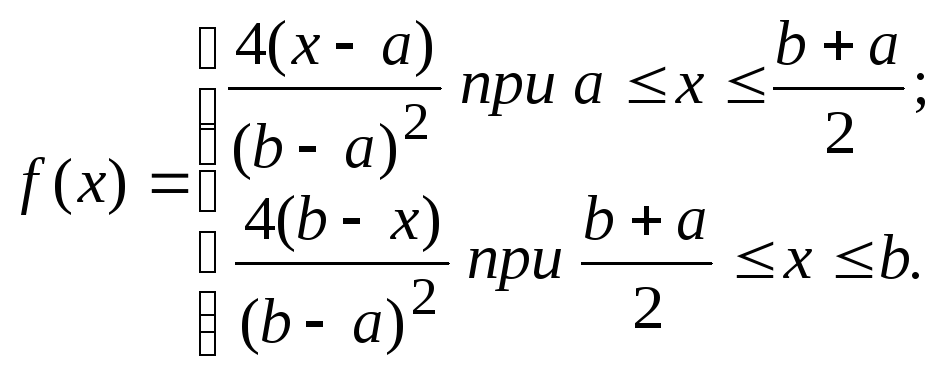
При иплотность,.

Математическое ожидание

.

Так как распределение симметрично относительно среднего значения, то мода и медиана совпадают с математическим ожиданием.

Дисперсия

.

Квадратичное отклонение

.

Ассиметрия из-за симметричности распределения.

Четвертый центральный момент

.

Эксцесс .

_{Рис.2.2. График плотности экспоненциального распределения при различных значениях параметра a.}

5.5.Биномиальное распределение

Дискретная случайная величина X, принимающая значения x_m=m,где

m=0,1,…,n,имеет биномиальное распределение, если вероятности её значений определяются следующей формулой:

. (5.5.1)

Здесь

-

число сочетаний из nпоm, а параметрp имеет смысл вероятности, то есть.

Это распределение связано с повторением опытов. Если в результате опыта событие Аимеет вероятностьpи опыт повторяетсяn раз, то вероятность того, что это событие произойдетm раз, рана. Действительно, конкретная реализацияnиспытаний, в которых событиеAпроизошлоmраз, а противоположное событиесоответственноn-mраз, имеет вероятность. Ноmсобытий средиn испытаний могут распределитьсяравновозможными способами. Отсюда и получается формула (5.5.1).

Сумма

,

так как q=1-p а. Выражениеявляется членом разложения бинома Ньютона(p+q)ⁿ ,поэтому это распределение называется биномиальным.

Математическое ожидание

. (5.5.2)

Дисперсия

. (5.5.3)

Квадратичное отклонение

. (5.5.4)

Если nустремить к бесконечности и одновременноpк нулю так, чтобы выполнялось соотношение

,

где а положительная константа, то в пределе

,

а это известное распределение Пуассона. То есть в пределе при ибиномиальное распределение совпадает с распределением Пуассона.

5.6.Распределение Пуассона

Рассмотрим дискретную случайную величину Х, которая может принимать только целые неотрицательные значения: 0, 1, 2, …

Говорят, что случайная величина Храспределена позакону Пуассона, если вероятность того, что она примет определённое значениеm, выражается формулой

где а– некоторая положительная величина, называемаяпараметром распределения Пуассона.

Ряд распределения по закону Пуассона:

	0	1	2	…	m
				…

Убедимся, что суммарная вероятность равна единице.

Но

Следовательно

Рис.5.6.1. Полигон распределения Пуассона.

Вычислим вероятность того, что Хокажется больше 0:

Математическое ожидание

Т.е. параметр а - есть математическое ожидание.

Дисперсия

Но

Следовательно .

.

Вывод. Дисперсия равна математическому ожиданию. Это свойство часто используют для определения, распределена ли случайная величина Х по закону Пуассона.

Рассмотрим типичную задачу. Пусть на оси Охслучайным образом распределяются точки. Пусть распределение удовлетворяет следующим условиям:

1. Вероятность попадания какого-либо числа точек в отрезок lзависит только от длины отрезка, но не от положения на оси. На единичный отрезок попадает в среднемточек.

2. Точки распределяются независимо.

3. Вероятность совпадения двух точек равна нулю (чем точки ближе, тем вероятность меньше).

Выделим на оси отрезок длиной lи рассмотрим дискретную случайную величинуХ– число точек, попадающих в этот отрезок. Возможные значенияХ: 0, 1, 2, …,m, …

Докажем, что случайная величина Х имеет закон распределения Пуассона. Для этого вычислим вероятность того, что на участок lпопадётmточек.

На участок хпопадётхточек. Это математическое ожидание. Поскольку участокхмал, то попадание двух точек в один отрезок пренебрежимо мало ихесть вероятность попадания одной точки на участокх.

Пусть существует число n,такое, что . Тогда вероятность попадания в один отрезок равна. А вероятность попадания вmотрезков равна

Обозначим , тогда

.

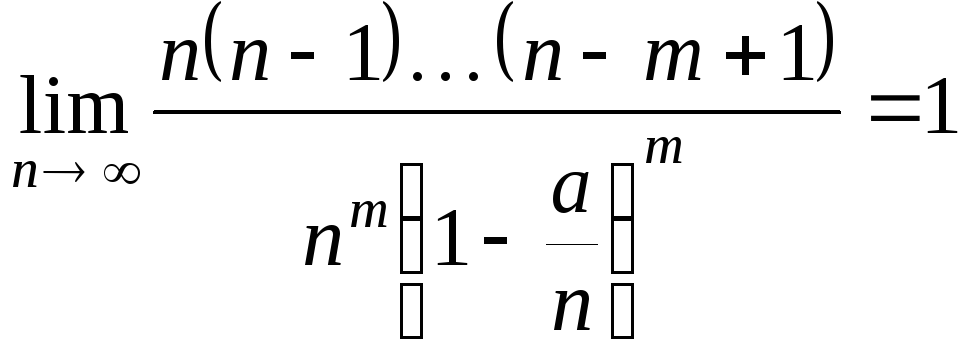
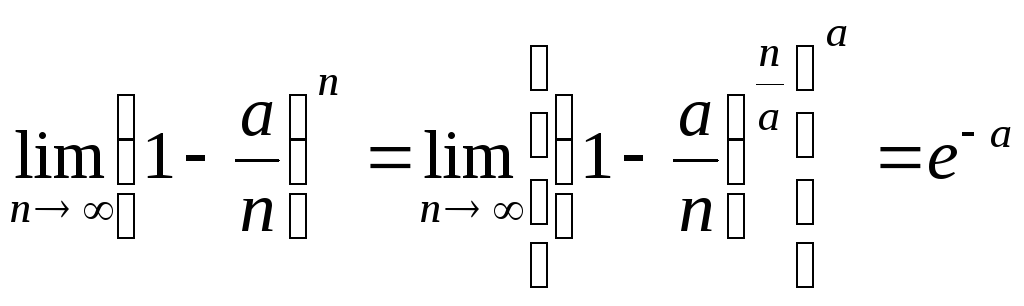
Что и требовалось доказать.

Мы убедились, что распределение Пуассона возникает там, где точки располагаются случайно друг от друга и подсчитывается их количество, попавшее в какую-то область. Мы рассмотрели одномерный случай, но его легко можно распространить на любую размерность. Например, если для отрезка оси параметр аравен, то для плоского случая(здесьS- площадь области), а для объёмного(V– объём области).

Докажем, что закон Пуассона является предельным для биномиального распределения.

Причём параметр .

Предельное свойство биномиального распределения можно записать в виде:

Если подставить , то получим

,

что уже было доказано. При большом nприближённо вероятность можно считать:

.

Из-за малой вероятности события закон Пуассона носит название “закона редких явлений”.