9.2.Проверка гипотезы о законе распределения

На практике часто приходится решать задачу определение закона распределения случайной величины. Эта задача решается так. Предполагается, что случайная величинаXраспределена по закону с плотностью гдеa,b– параметры распределения. Если эти параметры не известны, то их следует оценить по опытным данным, на пример, по методу наибольшего правдоподобия. Затем по опытным данным строится статистическая функция распределения или гистограмма и с использованием соответствующего критерия согласия проверяется соответствие теоретического закона распределения (гипотезы) статистическому закону распределения.

Между гипотезой и статистическим распределением неизбежны расхождения. Для ответа на вопрос, являются ли эти расхождения случайными, или закономерными следут воспользоваться соответствующим критерием согласия.

Таким образом, задача формулируется так: вводится гипотезаHчто величинаХимеет функцию распределенияf(a,b,x). Для того, чтобы принять или отвергнуть эту гипотезу рассмотрим некоторую величинуU, характеризующую степень расхождения между этим и статистическим распределением. Очевидно, что это есть случайная величина. Её закон распределения зависит от закона распределенияХ.

Допустим, что этот закон распределения нам известен. Обнаружено, что величина Uприняла значениеu.Спрашивается, можно ли объяснить это отклонение случайностью? Вычислим вероятность события . Если эта вероятность мала, то гипотезу Н следует отвергнуть, в противном случае – принять.

Оказывается, что при некоторых способах выбора U, её закон распределения обладает простыми свойствами и для достаточно больших выборок практически не зависит от закона распределения случайной величиныX.

Рассмотрим критерий согласия Пирсона - ².Предположим, что произведеноnнезависимых опытов, в каждом из которых случайная величинаХприняла определённое значение. Выделеныk интервалов, построена гистограмма распределения и оформлен статистический ряд.

Интервалы	х0;x1	х1 ;x2	…	xk-1;xk
pi*	p1*	p2*	…	pk*

Здесь x_i – границы интервалов,- опытные частоты.

Требуется проверить, согласуются ли экспериментальные данные с гипотезой о том, что случайная величина Химеет данный закон распределения.

Зная теоретический закон распределения, можно найти вероятности попадания случайной величины в каждый из разрядов:

Проверяя согласованность теории и статистики, будем исходить из расхождений между теоретическими вероятностями pи наблюдёнными частотамиp^*.Выберем в качествеU сумму квадратов отклонений.

с– веса разрядов берутся обратно-пропорциональными вероятностям разрядов.

При таком выборе коэффициентов мера расхождения обычно обозначается ²:

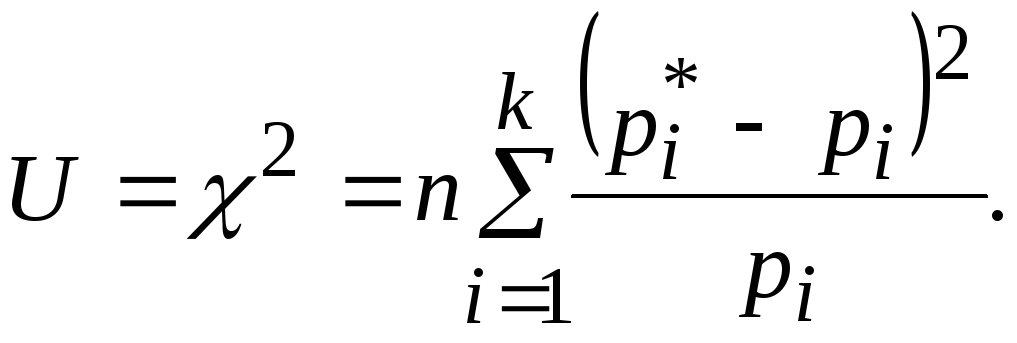
Учитывая, что

(9.2.1)

К.Пирсон показал, что U как случайная величина с ростомnимеет асимптотическое распределение с плотностью

. (9.2.2)

Это распределение называется распределениеми является частным случаем рассмотренного ранее гамма распределения (7.4.8) с параметрамииα=r/2. Единственный параметр распределенияrназываетсячислом степеней свободыи определяется по формуле

, (8.2.3)

где k –число интервалов в гистограмме, по которым сгруппированы данные выборки, аs– число условий, накладываемых на частотыp_i^*.

Примеры условий:

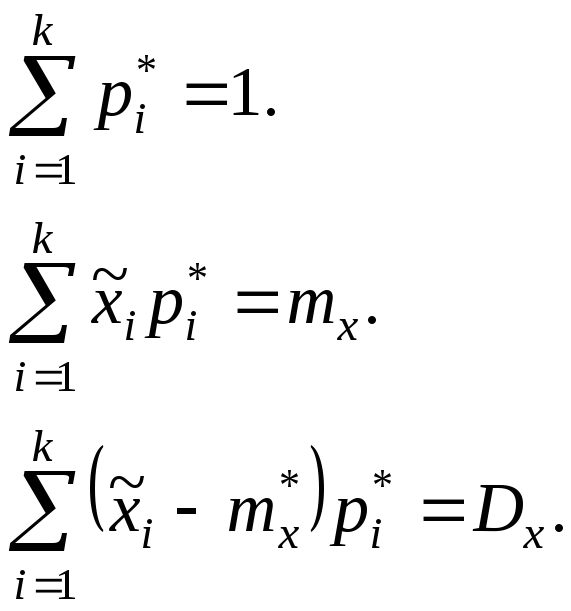
То есть число условий равно числу оцененных по выборке параметров плюс условие нормировки вероятностей к единице.

Для распределения ²составлены специальные таблицы, позволяющие по числу степеней свободыrи уровню значимостиопределить допустимое значение меры расхожденияUдля принятия гипотезы о законе распределения (гипотезыH).

Схема применения критерия ²:

1. Выборка значений случайной величины X разбивается по интервалам и строится статистический ряд и гистограмма.

2. Оцениваются параметры предполагаемого распределения.

3. Рассчитываются теоретические вероятности попадания случайной величины в соответствующие интервалы

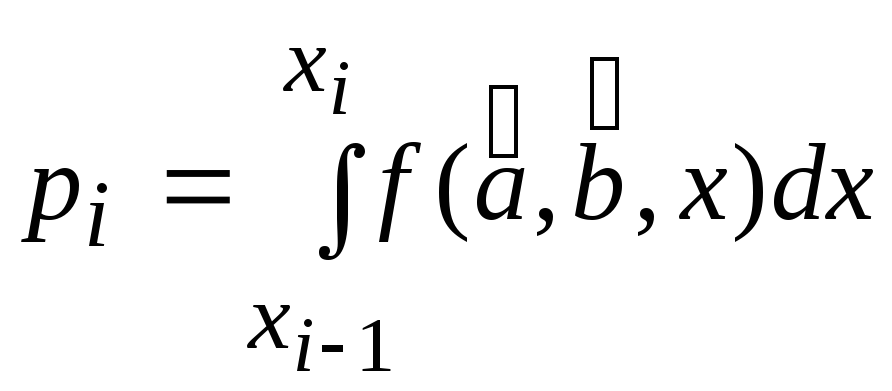. (9.2.4)

4. Определяется мера расхождения Uпо формуле (9.2.1).

5. Определяется число степеней свободы r по формуле (9.2.3).

6. Принимается соответствующее значение уровня значимости .

7. По иrпо таблице для распределения (9.2.2) определяется допустимое значение меры расхождения, где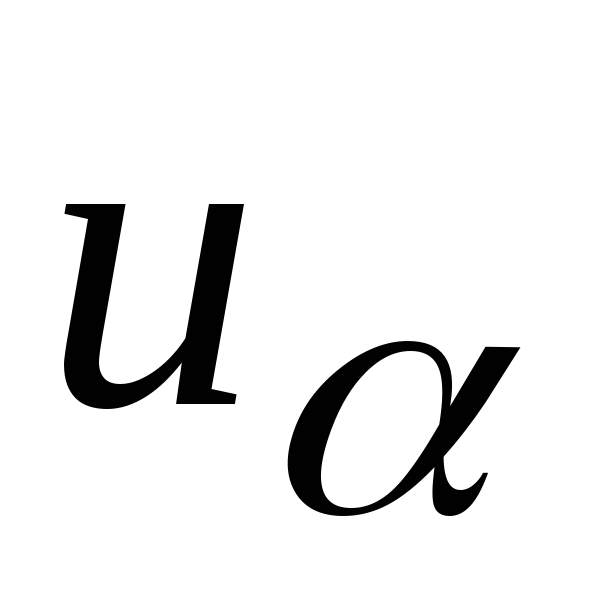удовлетворяет уравнению

. (9.2.5)

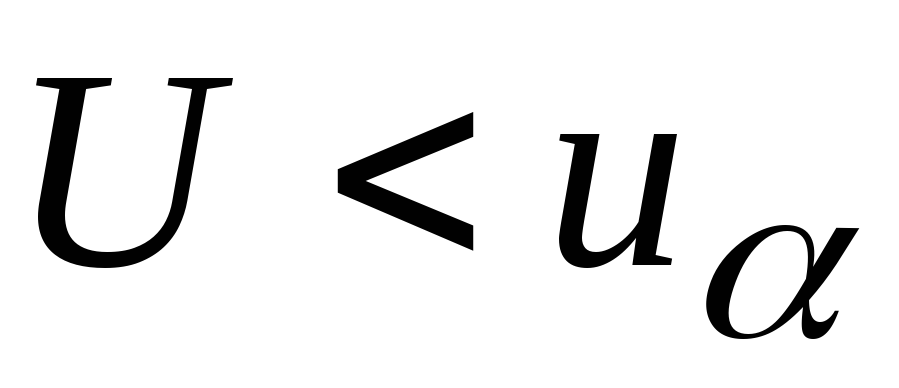8. Если ,то гипотеза о законе распределенияпринимается как непротиворечащая опытным данным. Если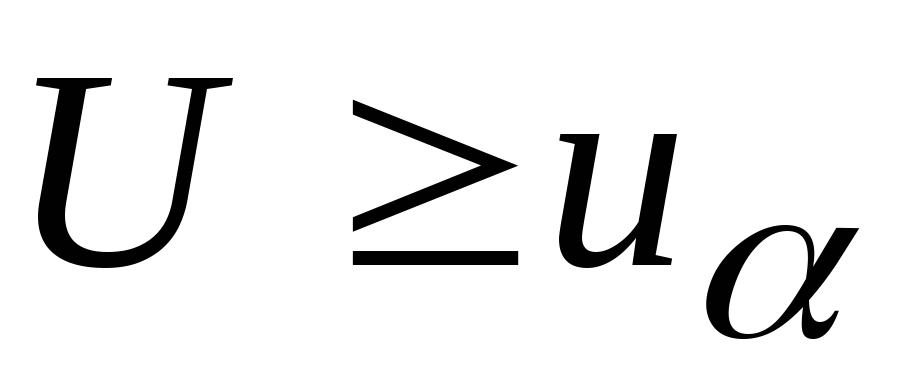, то гипотеза отбрасывается как неправдоподобная.

Пример. Имеется выборка реализаций случайной величины X объемом n=50:

7.42 6.65 9.00 7.89 7.37 6.52 8.07 6.92 6.37 6.12 7.13 6.03 7.08 8.05 6.37 8.33 6.47 6.99 9.01 7.02 7.49 6.20 6.46 7.81 7.66 5.88 7.72 8.28 6.89 5.95 8.28 9.03 7.34 8.17 8.33 6.79 7.56 7.64 7.82 6.81 6.00 8.66 8.51 7.22 6.46 7.54 7.73 5.20 7.82 7.18

Оценим параметры распределения в предположении, что случайная величинаX подчиняется закону Симпсона, для которого плотность распределения имеет вид:

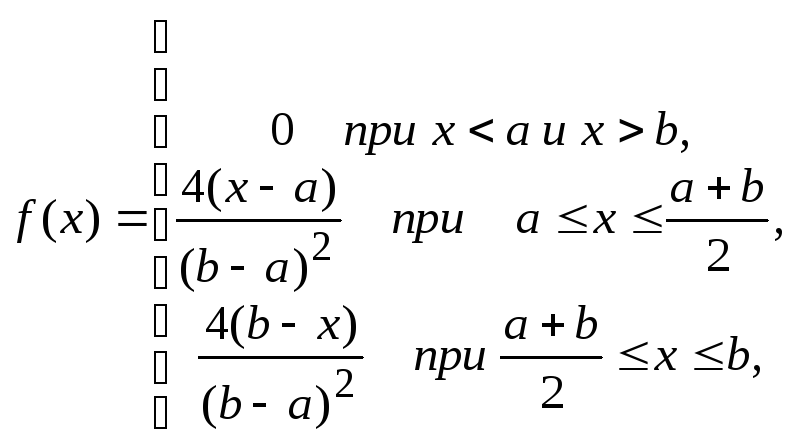
Это распределение имеет два параметра aиb, которые оценим по методу моментов из следующих уравнений:

.

По выборке реализаций случайной величины Хопределяем:

;

0.

Таким образом, для определения параметров aиb имеем два уравнения:

.

В результате решения этой системы получаем, что .

Построим теперь по выборке статистический ряд.

Крайние значения выборки . Размах выборки. Разобьем диапазон изменения значений выборки на 5 интервалов с шагом 1 от 5 до 10 и проведем группирование данных выборки по интервалам. Результаты такого группирования отражены в таблице9.2.1.

Таблица 9.2.1

Интервалы	От 5 до 6	От 6 до 7	От 7 до 8	От 8 до 9	От 9 до 10
mi	3	16	19	9	3
	0.06	0.32	0.38	0,18	0.06
	0.06	0.32	0.38	0,18	0.06
pi	0.082	0.289	0.396	0.207	0.026
npi	4.11	14.43	19.79	10.37	1.29
	0.302	0.171	0.031	0.180	2.246

m_i – это частотаi-го интервала (число данных выборки, попавшее вi-ый интервал);- частость (относительная частота или статистическая вероятность) значений выборки изi-го интервала;- теоретические вероятности попадания значения случайной величиныХ в соответствующий интервал, рассчитанные по формуле (9.2.4). Мера отклонения статистических вероятностей от теоретических, рассчитанная по формуле (9.2.1), равная сумме значений пятой строки таблицы 9.2.1,U=2.931.

Если принять уровень значимости , то пользуясь уравнением (8.2.5) или соответствующей таблицей для-распределения для отмеченного значенияα и числа степеней свободыr=5-3=2 получаем, что

Так как , то гипотеза о законе распределения Симпсона не противоречит опытным данным и ее можно принять.