13.Распределение функции случайных аргументов

13.1.Распределение функции одного аргумента

В предыдущей лекции мы определяли числовые характеристики функций от случайных аргументов. Но в некоторых случаях требуется знать и закон распределения функции от случайных аргументов.

Предположим по-прежнему, что между X и Y существует функциональная связь

(13.1.1)

и функция непрерывна, дифференцируема и монотонно возрастающая. Пустьи- функции распределения и плотности распределенияX и Y соответственно, тогда вероятность того, что равна вероятности того, что(см.рис.13.1.1), то есть

. (13.1.2)

Рис.13.1.1. Иллюстрация к выводу формулы (13.1.3).

Если разрешить функцию (13.1.1) относительно x , то есть

и подставить в правую часть (13.1.2), то получим, что

.

Дифференцируя полученное выражение по y, получаем:

.

Если функция (13.1.1) монотонно убывающая, то аналогичные рассуждения приводят к формуле

.

Обе эти формулы можно записать единообразно так:

. (13.1.3)

Пример 1. Пусть , тогда

.

Подставляем полученные результаты в (13.1.3) и получаем, что

.

Пример 2. Определим распределение случайной величины Y , если известно, что иX имеет плотность распределения

В данном случае .

, y>0 .

13.2.Распределение суммы случайных величин

Рассмотрим случай, когда третья случайная величина Z является суммой двух независимых случайных величин X и Y, то есть

.

Плотности этих величин соответственно. Плотность распределенияZ

. (13.2.1)

Этот интеграл называется сверткой или композицией плотностей и обозначается следующим образом:

.

Таким образом, если независимые случайные величины суммируются, то их плотности распределения свертываются.

Это правило распространяется на сумму любого числа независимых слагаемых. То есть, если

,

то

.

Пример. Определим плотность распределения суммы двух равномерно распределенных величин X₁ и X₂ c плотностями:

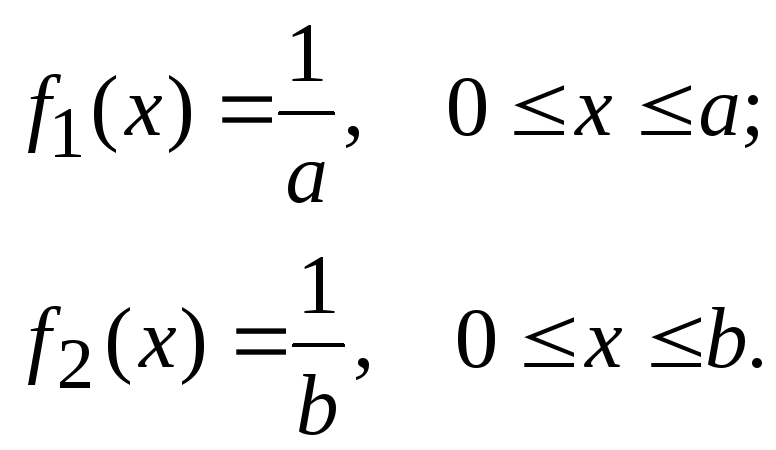
После подстановки этих плотностей в (13.2.1) и интегрирования в предположении получаем , что

Эта плотность называется трапециодальной (см. рис.13.2.1). Если , то трапеции вырождается в равнобедренный треугольник и соответствующая плотность называется плотностью Сипсона.

Рис.13.2.1.Трапециодальное распределение – свертка двух равномерных распределений.

13.3.Распределение суммы нормально распределенных случайных величин

Если , X и Y независимы и нормально распределены с плотностями

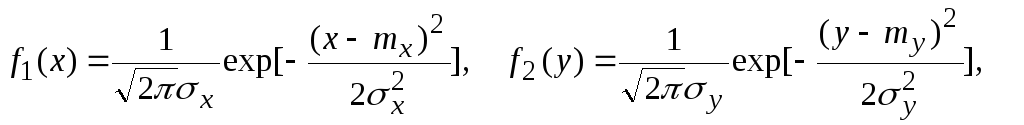то сумма Z будет распределена тоже нормально с плотностью

,

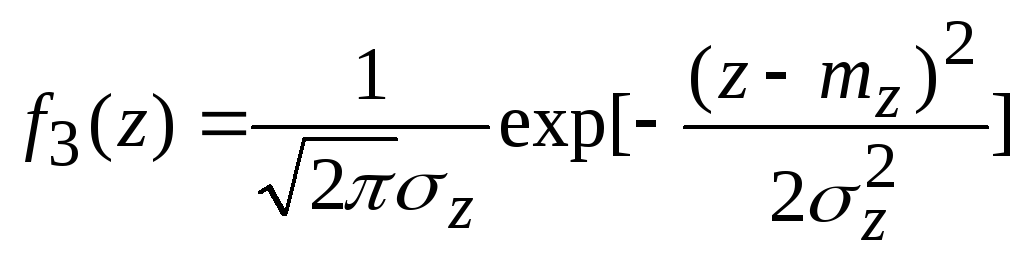где

.

Этот факт доказывается непосредственным интегрированием интеграла сверстки (13.2.1) после подстановки и.

Справедливо и более общее утверждение: если

, (13.3.1)

где иb- константы, а Х_i – независимые нормально распределенные случайные величины со средними значениями и дисперсиями, тоY будет распределено тоже нормально со средним значением

(13.3.2)

и дисперсией

. (13.3.3)

Отсюда вытекает, что если суммируются независимые нормально распределенные случайные величины, то сумма будет иметь тоже нормальное распределение с математическим ожиданием, равным сумме математических ожиданий слагаемых и дисперсией, равной сумме дисперсий слагаемых. То есть, если

,

то

. (13.3.4)

13.Распределение функции случайных аргументов

13.1.Распределение функции одного аргумента

В предыдущей лекции мы определяли числовые характеристики функций от случайных аргументов. Но в некоторых случаях требуется знать и закон распределения функции от случайных аргументов.

Предположим по-прежнему, что между X и Y существует функциональная связь

(13.1.1)

и функция непрерывна, дифференцируема и монотонно возрастающая. Пустьи- функции распределения и плотности распределенияX и Y соответственно, тогда вероятность того, что равна вероятности того, что(см.рис.13.1.1), то есть

. (13.1.2)

Рис.13.1.1. Иллюстрация к выводу формулы (13.1.3).

Если разрешить функцию (13.1.1) относительно x , то есть

и подставить в правую часть (13.1.2), то получим, что

.

Дифференцируя полученное выражение по y, получаем:

.

Если функция (13.1.1) монотонно убывающая, то аналогичные рассуждения приводят к формуле

.

Обе эти формулы можно записать единообразно так:

. (13.1.3)

Пример 1. Пусть , тогда

.

Подставляем полученные результаты в (13.1.3) и получаем, что

.

Пример 2. Определим распределение случайной величины Y , если известно, что иX имеет плотность распределения

В данном случае .

, y>0 .