5.7.Геометрическое распределение
Геометрическое распределение выражается следующим образом:
(5.7.1)
Название распределения связано с тем , что вероятности при различных n образу-ют геометрическую прогрессию со знаменателем , равнымq=1-p. Действительно
.
Параметр
p имеет смысл
вероятности. Пусть при повторении опыта
событиеАимеет вероятностьp,
тогда число опытовXдо первого появления событияА как
раз определяется выражением (5.7.1).
Действительно, вероятность того, что в
первыхn-1 опытах
событиеА не произойдет, равна(1-p)n-1
.А вероятность появления его приn-ом
испытании равнаp.Отсюда получаем, что вероятность
реализации такой серии событий равна
.
Математическое ожидание
.
Дисперсия
.
5.8.Распределение Паскаля
Распределение Паскаля дискретной случайной величины Хвыражается так:
, (5.8.1)
где
pиk– параметры распределения. Параметрpимеет смысл вероятности, то есть
.
Параметрk– целое
положительное число.
Математическое ожидание
.
Дисперсия
.
Это распределение связано, как и геометрическое, с повторением опытов.
Если p – вероятность событияА в одном опыте, то до появления этого событияkраз потребуется всегоk+xиспытаний, где конкретное значениеx имеет вероятность (5.8.1).
Это распределение обобщает геометрическое распределение. То есть если k=1, то распределение Паскаля совпадает с геометрическим. Действительно, если в (5.8.1) подставитьk=1, то получим
,
что совпадает с геометрическим распределением (5.7.1), если положить, что
x=n-1
и
учесть , что
.
5.9.Гипергеометрическое распределение
Гипергеометрическое распределение дискретной случайной величины Хвыражается так:
, (5.9.1)
где
N,n,k– целые положительные величины, играющие
роль параметров распределения, причем
,
.
Это выражение уже встречалось нам раньше в связи с выборкой размера n из партии деталей размеромN, в которойk-число дефектных деталей. Тогдаx- число дефектных деталей в выборке изn деталей, а (5.9.1) – вероятность этого значения.
Математическое ожидание
.
Дисперсия
.
5.10.Формула Стирлинга
При расчетах вероятностей в дискретных распределениях часто приходится вычислять выражение n!, например,
.
Стирлинг вывел удобную для практических расчетов приближенную формулу
. (5.10.1)
Эта формула особенно удобна при больших nно она дает хорошее приближения и при малыхn.На пример приn=2n!=2, а формула (5.10.1) дает значение 1.9. Приn=4 точное значение 4!=24, а приближенное 23.5. Приn=8 8!=40320 а приближенное значение 39902.4 с относительной ошибкой 0.01.
6.Непрерывные распределения
6.1.Нормальное распределение
Это наиболее часто встречающийся на практике закон распределения. Он характеризуется плотностью вероятности вида:
Кривая распределения по нормальному закону имеет симметричный холмообразный вид (см. рис.6.1.1)
Рис.6.1.1. Графики плотности нормального распределения при различных значениях квадратичного отклонения .
Максимальная
ордината кривой, равная
,
соответствует точке
;
по мере удаления от точкиmплотность распределения падает и
стремится к оси абсцисс.
Докажем, что m- есть математическое ожидание, а– есть среднее квадратическое отклонение. Для этого вычислим основные числовые характеристики случайной величиныХ.
Применим замену переменной
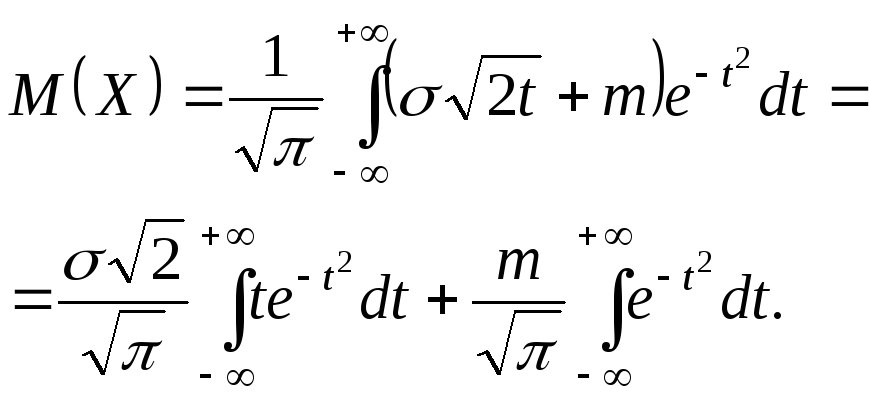
Первый интеграл равен нулю. Второй представляет собой интеграл Эйлера-Пуассона:
Следовательно,
.
На практике параметрmчасто называют центром рассеивания.
Вычислим дисперсию Х:
Та же замена переменной:
Интегрирование
по частям дает D(X)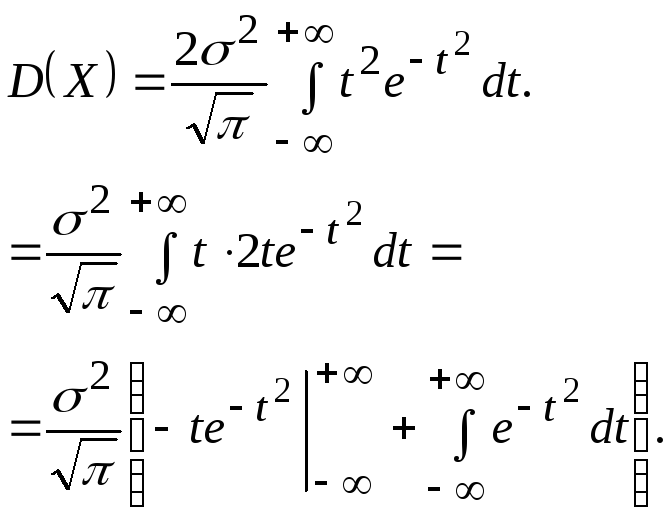
Первое
слагаемое равно нулю, второе
,
откуда
Геометрический смысл: m– центр симметрии кривой плотности распределения;- характеризует степень рассеивания случайной величины и одновременно расплывчатость кривой, поскольку площадь, ограниченная кривой плотности всегда равна единице. Размерностьmисовпадает с размерностью случайной величиныХ.Выведем общие формулы для центральных моментов любого порядка.
Делаем замену переменной
Интегрируем по частям:
Первый член в скобках равен нулю. Получаем:
Но момент степени S-2:
Следовательно
Т. е. можно выражать чётные моменты через моменты на 2 порядка ниже. Нечетные моменты в силу симметрии распределения равны нулю. Т. е. для чётных моментов имеем:
Общая формула для момента порядка Sпри чётномS:
,
где
под
понимается произведение всех нечётных
чисел от 1 доS-1.
Асимметрия:
Эксцесс:
Т.е. эксцесс характеризует крутость конкретного закона распределения по отношению к нормальному.
Вычислим вероятность попадания случайной величины Х, подчинённой нормальному закону с параметрамиm,на участок отдо.
где F(x)– функция распределения величины Х.
Замена переменной
Этот интеграл сложный, но существуют специальные таблицы для функций:
Ф*есть нормальная функция распределения. Её таблицы приведены в приложениях учебников и задачников.
Свойства функции Ф*:
Учитывая последнее свойство, рассмотрим вероятность попадания на участок, симметричный, относительно математического ожидания.
*
Решим следующую задачу. Отложим от математического ожидания четыре отрезка длиной и вычислим вероятность попадания случайной величины Х в каждый из них.
Вероятностью
попадания в четвёртый участок уже
практически можно пренебречь. Сумма же
вероятностей для первых трёх равна 0,5
с точностью до 0,01 (1%). Т. е. можно сказать,
что в интервале
укладывается практически всё рассеивание.
Такой способ оценки диапазона возможных
значений называетсяправилом трёх
сигм. Это правило позволяет грубо
оценить величину.
Берут максимально возможное отклонение
и делят его на три.
Часто (особенно в артиллерийской практике) для характеристики рассеяния кроме среднего квадратичного отклонения используют вероятное (срединное) отклонение, обозначается Е или В.
Вероятным (срединным) отклонениемслучайной величины Х, распределённой по нормальному закону, называется половина длины участка, симметричного относительно центра рассеивания, вероятность попадания в который равна 0,5.
Т.
е. вероятность попадания в интервал
равна 0,5.
Выразим Е через :
