7.2.Статистический ряд. Гистограмма

При большом числе наблюдений (порядка сотен) простая статистическая совокупность перестает быть удобной формой записи статистического материала - она становится слишком громоздкой и мало наглядной. Для придания ему большей компактности и наглядности статистический материал должен быть подвергнут дополнительной обработке - строится так называемый «статистический ряд».Предположим, что в нашем распоряжении результаты наблюдений непрерывной случайной величиныХ, оформленные в виде простой статистической совокупности. Разделим весь диапазон наблюдённых значений наинтервалыили«разряды» и подсчитаем количество значенийN_i, приходящееся на каждыйi-й разряд. Это число разделим на общее число наблюденийNи найдем частоту, соответствующую данному разряду:

Если разделить частоту на длину соответствующего интервала, то получим статистическую плотность

,

являющейся аналогом математической плотности распределения f(x).

Статистический ряд обычно представляется в виде следующей таблицы:

N интерв.	1	2	…	i	…	k
Интервал	x0,x1	x1,x2	…	xi-1,xi	…	xk-1,xk
Число случаев	N1	N2		Ni		Nk
Частота	P1*	P2*	…	Pi*	…	Pk*
Плотость			…		…

Статистический ряд часто также оформляется графически в виде так называемой гистограммы.Гистограмма строится следующим образом. По оси абсцисс откладываются разряды, и на каждом из разрядов как их основании строится прямоугольник, площадь которого равна частоте данного разряда. Для построения гистограммы нужно частоту каждого разряда разделить на его длину и полученное число взять в качестве высоты прямоугольника. В случае равных по длине разрядов высоты прямоугольников пропорциональны соответствующим частотам.

Из способа построения гистограммы следует, что полная площадь её равна единице.

Пример.1.Приведем гистограмму для длительностей простоя станков с числовым программным управлением (ЧПУ)T_Вв связи с восстановлением отказов, построенную по данным статистического ряда, приведенного в ниже следующей таблице. Объем выборкиN=193 достаточно большой, поэтому данные приведены в табл.7.2.1 в сгруппированном виде. Длина интервала 30 мин. Число интерваловk=15.

Таблица 7.2.1

Статистический ряд простоев станков с ЧПУ

N инт.	Интервал, мин	Число случаев	Частота	Плотность, 1/мин
1	0; 30	57	0.295	0.0098
2	30; 60	71	0.368	0.0122
3	60; 90	17	0.088	0.0029
4	90; 120	11	0.057	0.0019
5	120; 150	6	0.031	0.0010
6	150; 180	5	0.026	0.0009
7	180; 210	3	0.016	0.0005
8	210; 240	4	0.021	0.0007
9	240; 270	3	0.016	0.0005
10	270; 300	4	0.021	0.0007
11	300; 330	2	0.010	0.0003
12	330; 360	5	0.026	0.0009
13	360; 390	3	0.016	0.0005
14	390; 420	1	0.005	0.0002
15	420; 450	1	0.004	0.0002

По данным таблицы построен полигон распределения (рис.7.1.1) и гистограмма (рис.7.1.2).

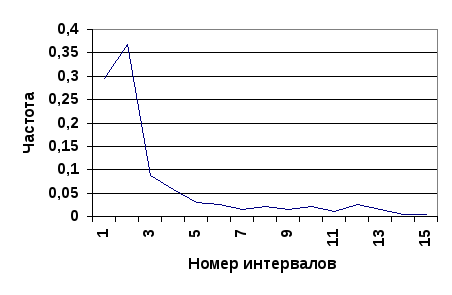
Рис.7.1.1.Полигон распределения

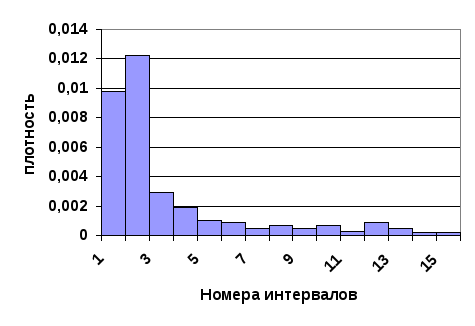
Рис.7.2.2. Гистограмма статистического распределения.

Очевидно, что при увеличении числа опытов можно выбирать всё более и более мелкие разряды; при этом гистограмма будет всё более приближаться к некоторой кривой, ограничивающей площадь, равную единице. Нетрудно убедиться, что эта кривая представляет собой график плотности распределения величины T_в.

Пользуясь данными статистического ряда, можно приближённо построить и статистическую функцию распределения величины T_в . Построение точной статистической функции распределения с несколькими сотнями скачков во всех наблюденных значениях трудоёмко и себя не оправдывает. Для практики обычно достаточно встроить статистическую функцию распределения по нескольким точкам. В качестве этих точек удобно взять границы разрядов, которые фигурируют в статистическом ряде. В этом случае

.

Соединяя полученные точки ломаной линией или плавной кривой, получим приближённый график статистической функции распределения. На рис.7.2.3 приведен такой график статистической функции распределения, построенный по данным табл.7.2.1.

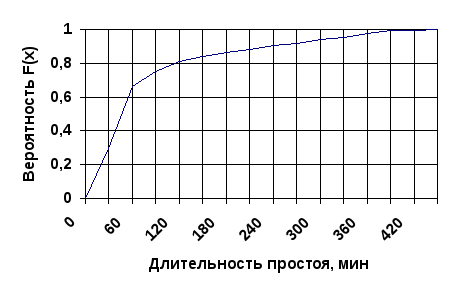
Рис.7.2.3.График статистической функции распределения.