6.2.Показательное распределение

Плотность и функция показательного распределенияположительной случайной величиныTвыражаются формулами:

(6.2.1)

соответственно, а– параметр распределения. График плотности представлен на рис.6.2.1. В литературе это распределение называют такжеэкспоненциальным.

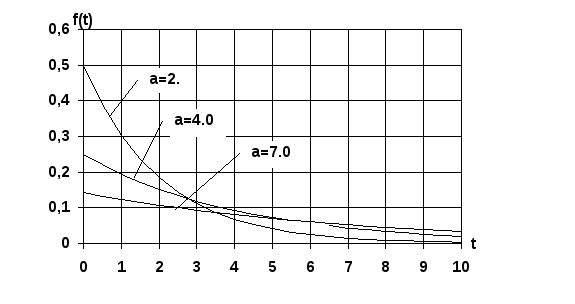
_{Рис6.2.1. График плотности показательного распределения при различных значениях параметра a.}

Математическое ожидание

.

Дисперсия

.

Квадратичное отклонение

,

то есть для показательного распределения математическое ожидание и квадратичное отклонение совпадают.

Этот закон широко используется в теории надежности благодаря свойству "отсутствия памяти" (марковскому свойству), которое значительно облегчает выкладки и упрощает расчетные формулы. Суть свойства в том, что вероятность безотказной работы объекта в заданном интервале не зависит от времени предшествующей работы.

Показательный закон является предельным для вероятности безотказной работы сложных систем, если система состоит из элементов, каждый из которых отказывает и восстанавливается независимо, но при отказе хотя бы одного элемента простаивает вся система. Такая ситуация на практике весьма распространена. Она имеет место, например, для сложных станков, автоматических линий и др.

6.3.Логарифмически нормальное распределение

Логарифмически нормальное распределение для положительной случайной величины Tимеет плотность

, (6.3.1)

где a иd- параметры распределения.

Рис.6.3.1.График плотности логарифмически нормального распределения при значениях параметров: a=1.0,d=(0.5, 1.0, 2.0)

Математическое ожидание

.

Дисперсия

Квадратичное отклонение

.

Коэффициент вариации

.

Ассиметрия

.

Мода

.

Функция распределения выражается через рассмотренную ранее функцию нормированного нормального распределенияследующим образом:

,

где

.

Здесь используется тот факт, что логарифм случайной величины T, распределенной по закону (6.3.1) имеет нормальное распределение с математическим ожиданиемa и дисперсиейd², по этому это распределение и называется логарифмически нормальным.

Если X имеет нормированное нормальное распределение то

будет иметь логарифмически нормальное распределение. После логарифмирования получаем, что

.

Медиана определяется из следующего уравнения:

,

решение которого -

.

Таким образом, параметр распределения a численно равен медиане распределения.

7.Статистическая оценка параметров распределения

Теория вероятности лишь описывает закономерности, имеющие место в массовых случайных явлениях природы. Разработка методов регистрации, описания и анализа статистических экспериментальных данных, получаемых в результате наблюдения массовых случайных явлений, составляет предмет науки – математической статистики. Все задачи математической статистики касаются вопросов обработки наблюдений над случайными явлениями. Можно выделить три основных типа таких задач:

1. Задача определения закона распределения случайной величины

2. Задача проверки правдоподобия гипотез

3. Задача нахождения неизвестных параметров распределения

7.1.Статистическая функция распределения

Предположим, что изучается некоторая случайная величина Х, закон распределения которой в точности неизвестен, и требуется определить этот закон из опыта или проверить экспериментально гипотезу о том, что величинаХподчинена тому или иному закону. С этой целью над случайной величиной Х производятся ряд независимых опытов (наблюдений). В каждом из этих опытов величинаХпринимает определенное значение. Совокупность наблюдённых значений величины и представляет собой первичный статистический материал, подлежащий обработке, осмыслению и анализу. Такая совокупность называется «простой статистической совокупностью» или «простым статистическим рядом». В литературе используется так же термин «выборка», имея ввиду, что из генеральной совокупности объектов берется выборка из нескольких объектов и над ними производятся соответствующие испытания или измерения. Обычно простая статистическая совокупность оформляется в виде таблицы с одним входом, в первом столбце которой стоит номер опытаi, а во втором — наблюдённое значение случайной величины.

Пример 1. Случайная величинаT- время восстановления отказа станка. Восстановлено 10 отказов, при восстановлении каждого из них затраченоT_iминут времени. Результаты наблюдений сведены в простой статистический ряд.

Табл.7.1.1.

Простой статистический ряд

i	1		2		3		4		5		6		7		8		9		10
Ti,мин		35		15		66		43		21		165		300		247		52		35

Простой статистический ряд представляет собой первичную форму записи статистического материала и может быть обработан различными способами. Одним из способов такой обработки является построение статистической функции распределения случайной величины.

Статистической функцией распределенияслучайной величиныTназывается частота событияT<tв данном статистическом материале. То есть

.

Для того чтобы найти значение статистической функции распределения при данном t,достаточно подсчитать число опытов, в которых величинаTприняла значение, меньшее чемt,и разделить на общее числоNпроизведенных опытов. То есть

,

где n(t)- число опытов, в которыхT<t.

Для построения графикаопытные данные располагают в возрастающем порядке, то есть

.

Такой упорядоченный ряд статистических данных называется вариационным рядом.- наименьшее значение,- наибольшее значение ,

размах выборки.

Пример 2. Построим статистическую функцию распределения для случайной величиныT из предыдущего примера.

Табл.7.1.2

Вариационный ряд

i	1	2	3	4	5	6	7	8	9	10
T(i)	15	21	35	35	43	52	66	165	247	300

Размах выборки R=300-15=285 мин

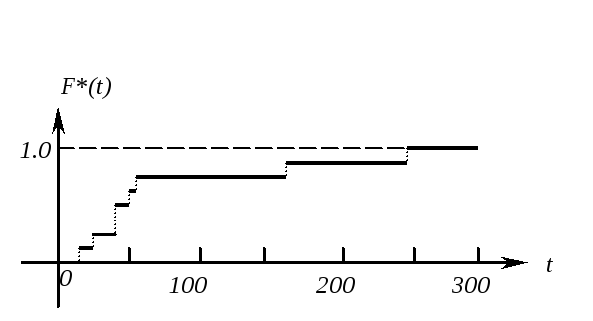
Рис.7.1.1.График статистической функции распределения