8.Метод наибольшего правдоподобия

Рассмотренный выше метод моментов приводит обычно к относительно простым формулам для оценки параметров, однако в ряде случаев эти оценки малоэффективны или вовсе несостоятельны. Например, для применения метода моментов теоретические моменты должны существовать, что не для всех распределений выполняется. Например, у распределения Коши, имеющего плотность

,

все моменты бесконечны.

Распределение Фреше

имеет конечные моменты только порядка n<b,а именно начальные моменты

.

Это значит, что методом моментов для оценки параметров а иb можно воспользоваться, еслиb>2. Но так как значение параметраb еще нужно определить, то использования метода моментов становится проблематичным.

Поэтому необходимы и другие методы, лишенные отмеченных недостатков.

Метод наибольшего правдоподобия обладает важным достоинством: он всегда приводит к состоятельным оценкам, имеющим наибольшую точность. Этот метод наилучшим образом использует всю информацию о неизвестных параметрах распределения, имеющуюся в выборке. Однако на практике он часто приводит к необходимости решать весьма сложные системы уравнений.

Метод наибольшего правдоподобия был предложен Р.Фишером, одним из основоположников математической статистики и является наиболее обоснованным и проверенным методом, широко используемом в математической статистике.

8.1.Случай дискретных распределений

Рассмотрим случай оценки параметра распределения дискретной случайной величины X, вероятности значений которой определяются согласно распределению, где- неизвестный параметр, который нужно оценить по выборке.

Функция

называется функцией правдоподобия. Если число случаев, когда случайная величина Xприняла значенияравно соответственно, где- размер выборки, то функция правдоподобия

. (8.1.1)

Согласно методу наибольшего правдоподобия в качестве оценки неизвестного параметра принимается то значение, при котором функция правдоподобия принимает наибольшее значение для данной выборки. То есть в качестве оценки дляберется наиболее вероятное значение для данной выборки.

Это значение находится в результате решения уравнения

.

Практически удобнее находить максимум функции ln(L), тогда соответствующее уравнение примет вид:

. (8.1.2)

Это уравнение принято называть уравнением правдоподобия.Решение этого уравнения дает максимум функции правдоподобия, если для него выполняется условие

.

Если распределение имеет два пара параметра и, то есть имеет вид, то для оценки этих параметров используются система из двух уравнений правдоподобия:

. (8.1.3)

При большем числе параметров число подобных уравнений соответственно увеличивается.

Проиллюстрируем применение метода наибольшего правдоподобия на примерах.

Пример 1. Приn-кратном повторении опыта событиеАпроявилосьm раз. Оценим вероятность событияАпо методу наибольшего правдоподобия. Будем считать, что случайная величинаX принимает значение 1, если произошло событиеАи 0, если произошло противоположное событие.

Согласно (8.1.1) функция правдоподобия в данном случае имеет вид:

,

где - оцениваемая вероятность.

После логарифмирования получаем, что

.

После дифференцирования по получаем следующее уравнение:

,

после решения которого получаем, что

. (8.1.4)

Крышечкой сверху будем отличать оценку параметра от его точного значения.

Формула (8.1.4) уже известна из предыдущего изложения - это оценка вероятности как частоты события A. Эта оценка состоятельна, то есть приона сходится к вероятности этого события, то есть

. Эта оценка также эффективна, то есть не существует других более эффективных оценок. Оценка так же несмещенная, то есть её математическое ожидание равно точному значению параметра:Об этих свойствах оценок подробнее поговорим позже.

Пример 2. Рассмотрим случай оценки параметра дискретной случайной величиныХ,распределенной по закону Пуассона

Согласно (8.1.1) функция правдоподобия равна

.

После логарифмирования получаем

.

После дифференцирования получаем:

,

Откуда

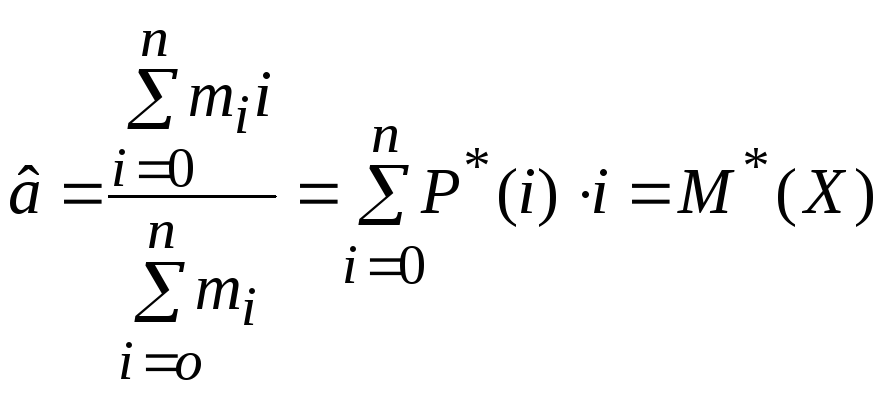, (8.1.5)

где - статистическая вероятность того, чтоX=i.

Таким образом, в качестве оценки параметра араспределения Пуассона следует брать статистическое среднее выборки.

Пример 3.Рассмотрим случай оценки параметра геометрического распределения дискретной случайной величиныX, которое задается законом

.

Если значение в выборке размеромN,встретилосьm_iраз, то функция правдоподобия

.

.

После дифференцирования получаем:

.

В результате решения этого уравнения получаем оценку для параметра p

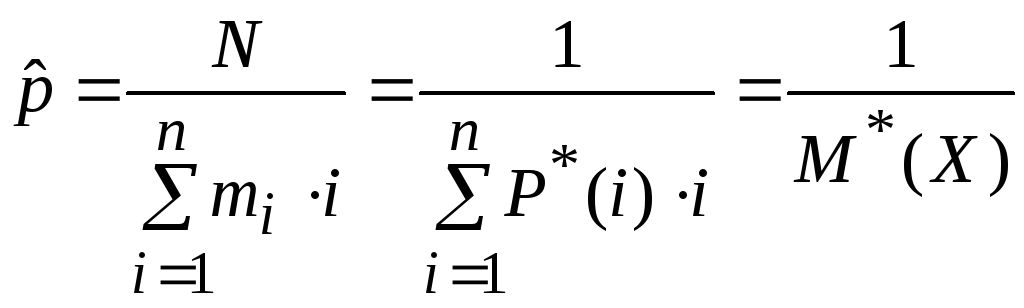. (8.1.6)

Здесь - статистическая вероятность того, что.

Таким образом, оценкой наибольшего правдоподобия параметра pгеометрического распределения является величина, обратная выборочному среднему.