3.4.Формула полной вероятности.

Следствием теорем сложения и умножения вероятностей является формула полной вероятности.

Пусть требуется определить вероятность некоторого события А,которое может произойти вместе с одним из событий, образующих полную группу несовместимых событий. Будем называть эти событиягипотезами. Тогда имеет место следующая формула:

(3.9)

Доказательство. Событие А может появиться только в комбинации с какой-либо гипотезой Н_i:

Так как гипотезынесовместимы по условию, то и событиятоже несовместимы и к ним применима теорема сложения вероятностей, то есть

Но по теореме умножения , поэтому получим, что и требовалось доказать.

Пример1. Имеются три одинаковые на вид урны; в первой урне два белых и один чёрный шар; во второй – три белых и один чёрный; в третьей – два белых и два чёрных шара. Выбираем наугад одну из урн и вынимает из неё шар. Найти вероятность того, что этот шар белый.

Решение. Рассмотрим три гипотезы: Н1 – выбор первой урны; Н2 – выбор второй урны; Н3 – выбор третьей урны и событие А – появление белого шара.

Пример 2. При обработке детали выполняется три различные технологические операции. Вероятности брака на каждой из трех операций равны:p₁=0.01,p₂=0.012,p₃=0.009 соответственно. Брак можно исправить:cвероятностьюq₁=0.5, если он возник только на одной операции; с вероятностьюq₂=0.2, если он возник только на двух операциях. Брак неисправим, если он возник на всех трех операциях. Требуется рассчитать вероятность неисправимого брака детали после выполнения всех трех операций.

Решение. Рассмотрим четыре события (гипотезы):

H₀- брак на всех операциях не произошел (деталь годная);

H₁- брак только на одной операции;

H₂- брак только на двух операциях;

H₃- брак на всех трех операциях.

Пользуясь теоремами сложения и умножения вероятностей, определим вероятности отмеченных гипотез.

Условные вероятности события А:

.

Пользуясь формулой полной вероятности (3.9), получаем, что

.

3.5.Формула Бейеса или теорема гипотез.

Пусть имеется полная группа несовместных гипотез . Вероятности этих гипотез до опыта известны и равны соответственно. Произведён опыт, в результате которого появилось событиеА.Как изменятся вероятности гипотез в связи с появлением этого события? Т.е. надо найти.

Окончательно получаем

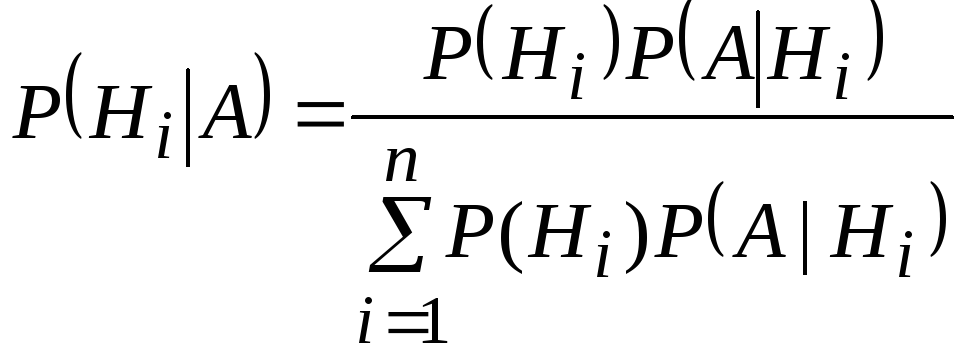. (3.10)

Пример 1.Прибор может собираться из высококачественных деталей и деталей обычного качества; вообще около 40% приборов собирается из высококачественных деталей. Если прибор собран из высококачественных деталей, его надёжность (вероятность безотказной работы) равна 0.95. Если из деталей обычного качества, то 0.7. Прибор испытывался в течениеt часов и работал безотказно. Найти вероятность того, что он собран из высококачественных деталей.

Решение. Возможны две гипотезы: Н₁- прибор собран из высококачественных деталей,Н₂– прибор собран из обычных деталей.

Вероятности этих гипотез до опыта:

В результате опыта наблюдено событие А– прибор безотказно работал времяt. Условные вероятности при гипотезахН₁иН₂равны:

.

По формуле Бейеса находим:

.

Пример 2. Партия деталей обрабатывалась на двух станках, 40% на первом станке и 60% на втором станке. Вероятность брака при обработке на первом станкеp₁=0.01, а при обработке на втором станке р₂=0.02. При проверке детали она оказалась бракованной (событиеА). Определить вероятность того, что деталь была обработана на первом станке, если не известно на каком станке она обрабатывалась.

Решение. Имеются две гипотезы:

H₁– деталь была обработана на первом станке;

H₂– деталь была обработана на втором станке.

Априорные (начальные) вероятности этих гипотез

.

Вероятности

.

Пользуясь формулой Бейеса (3.10) получаем:

.

Таким образом, вероятность того, что деталь была обработана на первом станке, равна 0.25.