14.2.Неравенство Чебышева

Чебышев доказал неравенство, лежащее в основе доказательства законов больших чисел. Это неравенство утверждает, что если случайная величина X имеет математическое ожидание m_x и дисперсию D_x, то каково бы не было положительное число α , вероятность того, что X отклоняется от своего математического ожидания не меньше чем на α, ограничена сверху величиной :

. (14.2.1)

Доказательство. Если - плотность распределенияX, то

,

.

Первое неравенство справедливо, так как сужается область интегрирования, а второе неравенство справедливо, так как в области интегрирования. Из этих неравенств получаем, что

,

что эквивалентно (14.2.1).

Пример. Оценим сверху вероятность того, что случайная величина со средним значением и квадратичным отклонением отклонится от среднего значения больше чем на 3.

Решение. В этом случае . Из неравенства Чебышева получаем, что

.

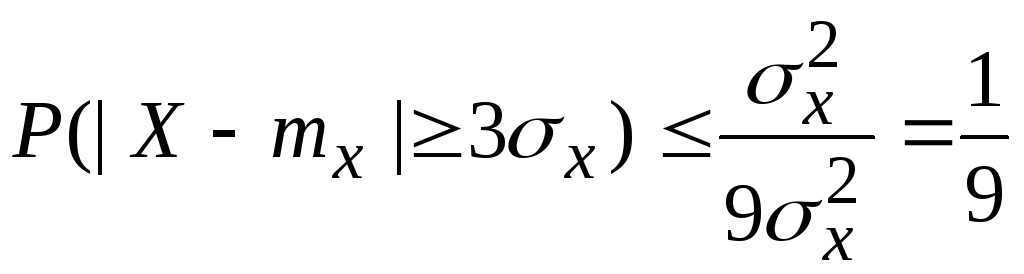Практическое значение неравенства Чебышева невелико, так как оно дает слишком общую и поэтому неточную оценку для вероятности отклонения. Например, для нормального распределения с такими же параметрами отмеченная в примере вероятность равна 0.003, что конечно меньше 1/9, но слишком далеко от этой верхней оценки, даваемой неравенством Чебышева.

14.3.Закон больших чисел Чебышева

Пусть - реализации случайной величиныX. Среднее арифметическое значение этих реализаций

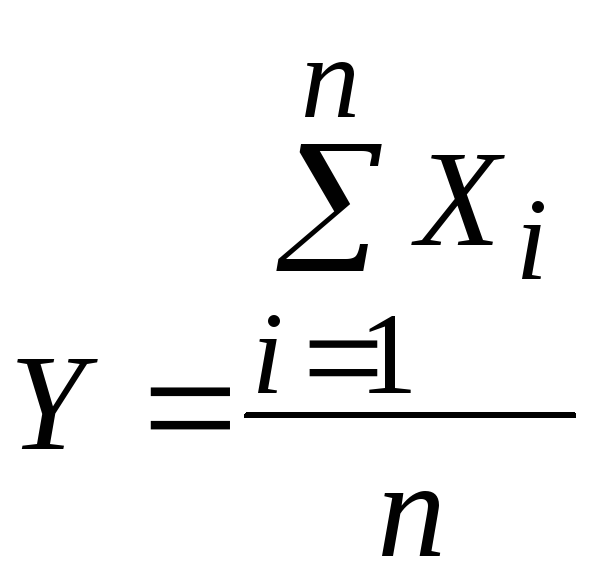(14.3.1)

тоже является случайной величиной со средним значением

(14.3.2)

и дисперсией

. (14.3.3)

Отсюда вытекает, что дисперсия среднего арифметического значения выборки с ростом выборки стремится к нулю, а среднее арифметическое становится все ближе к математическому ожиданию .

Чебышев этот факт сформулировал в виде теоремы: при достаточно большом числе независимых опытов среднее арифметическое наблюденных значений случайной величины сходится по вероятности к ее математическому ожиданию.

В виде формулы сказанное запишется так: при увеличении n среднее арифметическое стремится по вероятности кm_x , то есть

, (14.3.4)

где - произвольные малые положительные числа.

Доказывается этот факт с использованием неравенства Чебышева, если применить его к случайной величине (14.3.1).

Марков сделал обобщение результата Чебышева. Если у Чебышева предполагалось, что случайные величины X_i одинаково распределены, то Марков рассмотрел случай, когда X_i от опыта к опыту могут изменять закон распределения, оставаясь независимыми.

Результат Маркова состоит в следующем: если независимые случайные величины

имеют математические ожидания

и дисперсии

ограниченные величиной L, то есть

,

то при возрастании n среднее арифметическое значение наблюденных величинсходится по вероятности к среднему арифметическому их математических ожиданий, то есть к величине

.

14.4.Центральная предельная теорема

Рассмотренные варианты закона больших чисел говорят о сходимости к некоторой величине. Однако есть еще “количественная форма закона больших чисел”, когда рассматривается сходимость к случайной величине с определенным законом распределения. Так центральная предельная теорема говорит об условиях сходимости распределения суммы случайных величин к нормальному закону распределения.

Центральная предельная теорема для одинаково распределенных независимых случайных величин формулируется так: если -независимые случайные величины с одинаковым законом распределения и с математическим ожиданиемm и дисперсией , то при неограниченном увеличенииn закон распределения суммы

неограниченно приближается к нормальному закону с математическим ожиданием

и дисперсией

.

Справедлив и более общий результат, когда слагаемые X_i имеют различные законы распределения, важно только, чтобы дисперсии у них не слишком отличались друг от друга, например, не превышали некоторую конечную величину L. В этом случае с ростом числа слагаемых n сумма будет иметь распределение, неограниченно приближающееся к нормальному с математическим ожиданием

(14.4.1)

и дисперсией

. (14.4.2)