Функция |
23 |
Пример. |
|
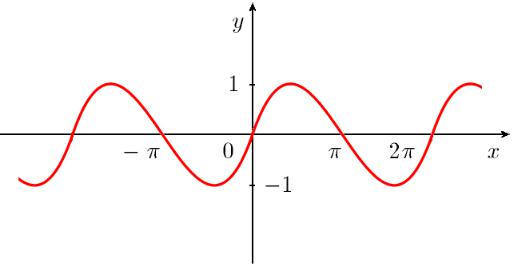
Из школьного курса элементарной математики известно, что функция |
y = sin x |
является периодической с периодом T = 2π. |
|
3.5.1.График функции y = sin x. Она является 2π периодической.
3.6.Ограниченная функция
Определение 3.6.1.
Функция y = f(x) называется ограниченной снизу на множестве D0, åñëè
существует такое число m, ÷òî f(x) > m ïðè x D0. Число m при этом называется нижней границей функции.
Определение 3.6.2.
Функция y = f(x) называется ограниченной сверху на множестве D0, åñëè
существует такое число M, ÷òî f(x) 6 M ïðè x D0. Число M при этом называется верхней границей функции.
Определение 3.6.3.
Функция y = f(x) называется ограниченной на множестве D0, если она ограничена на нем и снизу, и сверху.
Функция |
24 |
Замечания.
1.В этих определениях мы предполагаем, что D0 D, ãäå D область определения функции.
2.Если существует такое число M, ÷òî |f(x)| 6 M ïðè x D0, то функция f(x)
является ограниченной на множестве D0, поскольку тогда −M 6 f(x) 6 M, а значит, в качестве нижней границы можно взять число
проверить, и обратное утверждение: если функция f(x)
òî |f(x)| 6 M.
3.Если число m является нижней границей функции, то любое другое число m1, удовлетворяющее неравенству m1 < m, также является ее нижней границей. Аналогично обстоит дело и с верхней границей: если M верхняя граница функции, то любое другое число M1 > M также является ее верхней границей.
4.Самую большую из всех нижних границ принято называть точной нижней границей функции, а самую маленькую из ее верхних границ точной верхней границей. Отметим, что в общем случае у ограниченной функции обязательно существуют точная нижняя и точная верхняя граница, но вот вопрос о том, достигает ли функция своих точных границ, является довольно тонким. Мы его рассматривать не будем.
Рис. 3.6.1. Эта функция на отрезке [a, b] ограничена. Ее точная нижняя граница на нем равна m, а точная верхняя граница M.
Функция |
25 |
Примеры. |
|
1. Функция y = sin x является ограниченной при |
x, ò. ê. |sin x| 6 1 ïðè x. |
В этом примере −1 точная нижняя граница функции, а 1 ее точная верх-
няя граница. Числа −2 è 2 также являются соответственно нижней и верхней границами данной функции, но не являются ее точными границами.
2.Функция y = 1/x является ограниченной на отрезке [1, 2], но не является таковой на отрезке [−1, 1], поскольку в точке x = 0 этого отрезка она не определена.
3.7. Суперпозиция функций
Пусть заданы функции y = f(z) è z = g(x). Тогда можно рассматривать и функцию
y = f(g(x)) = F (x), которая называется сложной функцией èëè суперпозицией функций f è g.
При этом, разумеется, необходимо еще разобраться с областями определения и множествами значений исходных функций и их суперпозиции. Нетрудно убедиться, что в этом
вопросе не возникнет никаких проблем, если f : Z Y è g : X Z, т. е. область
определения функции f совпадает с множеством значений функции g. В результате
для суперпозиции оказывается, что F : X Y.
Пример.
Если заданы функции y = sin z è z = x3, то существует и суперпозиция этих
функций y = sin x3, которая определена на множестве вещественных чисел. Ее
множеством значений является отрезок [−1, 1].
3.8. Обратная функция
Пусть задана некоторая функция y = f(x), определяющая зависимость y îò x. Ïðåä-
положим, что нам удалось поменять ролями y è |
x. Тогда получится, что x зависит |
îò y, и мы приходим к функции x = f−1(y), |
которую называют обратной äëÿ |
функции y = f(x). |
|
Пример. |
|
Если задана функция y = x3, то функция x = √3 y будет для нее обратной.
Функция |
26 |
Замечания.
1.Обозначение f−1 для обратной функции является общепринятым, но такую за-
пись нельзя трактовать как возведение функции f в минус первую степень. Это просто обозначение и не более того.
2.Наше предположение о возможности смены ролей y è x обоснованным не яв-
ляется, причем отнюдь не только по формальным причинам, связанным с тем, что мы ни слова не сказали об области определения и о множестве значений ис-
ходной и обратной функции. Это хорошо иллюстрирует пример функции y = x2, для которой наши рассуждения приводят к зависимости x = ±√y, которую мы не можем считать функцией, иначе получилось бы, что для нее одному значе-
нию аргумента y соответствуют два значения функции x, а это противоречит определению 3.2.1.
3.Из сказанного выше следует, что обратная функция существует далеко не у каждой функции. Этот вопрос в целом является совсем не простым. Безупречно строгое определение обратной функции является достаточно абстрактным и сложным. Мы его рассматривать не будем, отсылая читателей к литературе, где данный вопрос излагается в полном объеме.
Рис. 3.8.1. Графики взаимно обратных функций y = x3 (серая кривая)
√
è y = 3 x (красная кривая) располагаются симметрично относительно биссектрисы первого и третьего координатных углов.
Очевидно, что в случае, когда у некоторой функции y = f(x) существует обратная
функция x = f−1(y), графики этих функций совпадают, поскольку они фактически