
- •1.1. Как пользоваться этим учебником
- •1.2. О курсе высшей математики
- •1.3. Биология, почвоведение и математика
- •2. Базовые понятия
- •2.1. Множества
- •2.2. Высказывания
- •2.3. Кванторы
- •2.4. Системы координат
- •2.5. Абсолютная величина числа
- •3. Функция
- •3.1. Величины постоянные и переменные
- •3.2. Определение функции
- •3.3 Способы задания функции
- •3.5. Периодическая функция
- •3.6. Ограниченная функция
- •3.7. Суперпозиция функций
- •3.8. Обратная функция
- •3.9. Неявная функция
- •3.10. Однозначная и многозначная функция
- •3.11. Рекомендации
- •3.12. Вопросы для самоконтроля
- •4. Предел функции
- •4.1. Определение предела функции
- •4.3. Бесконечно малая величина
- •4.4. Бесконечно большая величина
- •4.5. Свойства пределов
- •4.6. Неопределенность вида 0/0
- •4.7. Неопределенность вида ∞/∞
- •4.9. Первый замечательный предел
- •4.10. Второй замечательный предел
- •4.11. Основные теоремы о пределах
- •4.12. Рекомендации
- •4.13. Вопросы для самоконтроля
- •5.1. Приращения аргумента и функции
- •5.2. Два определения непрерывности
- •5.3. Точки разрыва и их классификация
- •5.4. Свойства непрерывных функций
- •5.5 Рекомендации
- •5.6. вопросы для самоконтроля
- •6. Производная функции
- •6.1. Определение производной
- •6.2. Геометрический смысл производной
- •6.3. Механический смысл производной
- •6.4. Основные теоремы о производных
- •6.5. Производные элементарных функций
- •6.6 Сводка формул
- •6.7. Примеры на вычисление производной
- •6.8. Производные высших порядков
- •6.9. Рекомендации
- •6.10. Вопросы для самоконтроля
- •7. Приложения производной
- •7.1. Возрастание и убывание функции
- •7.2. Экстремумы функции
- •7.3. Наибольшее и наименьшее значения функции на промежутке
- •7.4. График функции
- •7.5. Уравнение касательной
- •7.6. Приближенные решения уравнений
- •7.7. Правила Лопиталя
- •7.8. Рекомендации
- •7.9. Вопросы для самоконтроля
- •8. Дифференциал функции
- •8.1. Определение дифференциала функции
- •8.2. Свойства дифференциала
- •8.3. Геометрический смысл дифференциала
- •8.4. Рекомендации
- •8.5. Вопросы для самоконтроля
- •9. Примеры контрольных работ
- •11. Формулы
- •11.1. Основные свойства степени
- •11.2. формулы сокращенного умножения
- •11.3. Квадратное уравнение
- •11.4. Разложение квадратного трехчлена на множители
- •11.5. Основные свойства логарифмов
- •11.6. Тригонометрические формулы
- •12 Литература
- •13. Об авторах этого учебника
- •14. Предметный указатель

6 |
Производная функции |
73 |
|
|
|
Мы приступаем к изучению основ дифференциального исчисления. Эту тему без преувеличения можно назвать самой важной темой всего курса высшей математики. В рамках этой темы мы рассмотрим такие основополагающие понятия, как производная и дифференциал функции, а также изучим их основные свойства.
Идеи дифференциального исчисления зародились еще в XV II веке в работах двух
великих ученых Ньютона и Лейбница. Эти идеи получили очень мощное развитие в исследованиях их многочисленных последователей, прежде всего, математиков и физиков, и привели к значительным открытиям в самых различных разделах естествознания, в том числе в биологии и почвоведении.
6.1. Определение производной
Определение 6.1.1.
Производной функции y = f(x) в некоторой фиксированной точке x называется предел отношения приращения функции 4f = f(x + 4x) − f(x) к прира-
щению аргумента 4x, когда последнее стремится к нулю:
f 0(x) = lim |
4f |
= lim |
f(x + 4x) − f(x) |
. |
4x→0 |
4x |
4x→0 |
4x |
|
Анимация
Замечания.
1.Напомним, что приращение аргумента 4x это просто некоторая переменная величина, имеющая числовые значения. Значению аргумента x соответствует значение функции f(x), а значению аргумента x + 4x соответствует значение
функции f(x + 4x). Разность 4f = f(x + 4x) − f(x) между этими двумя зна- чениями функции и называется ее приращением, соответствующим приращению аргумента 4x.

Производная функции |
74 |
2.Предел, который используется в данном определении, может и не существовать (см. замечания на стр. 36). В этом случае говорят, что в данной точке x произ-
водная функции y = f(x) не существует (см. пример 6.1.3 íà ñòð. 75).
3.Для простоты мы опустили в этом определении требование, чтобы функция f(x)
была определена на некотором интервале (a, b), содержащем точку x. Îíî íåîá-
ходимо, чтобы мы имели право рассматривать значение функции в точке x+4x.
4.Когда значение аргумента x меняется, значение производной f 0(x) также меняется. Поэтому саму производную функции y = f(x) также можно рассматривать как некоторую функцию. При этом, однако, область определения f 0(x) может
оказаться уже, чем область определения f(x), поскольку для каких-то значений аргумента производная может и не существовать.
5.Для производной нередко используются и другие обозначения:
f 0(x) = f 0x(x) = dxdf = dfdx(x).
Такая форма записи предполагает, что мы рассматриваем производную как функцию аргумента x. Если же нам потребуется указать, что производная ищется
для какого-то конкретного значения x0 аргумента x, то мы будем использовать следующие обозначения:
f 0(x0) = f x0 (x0) = f 0(x) x=x0 |
= dx x=x0 . |
||
|
|
df |
|
|
|
|
|
|
|
|
|
Определение 6.1.2.
Функция y = f(x) называется дифференцируемой в некоторой фиксирован-
ной точке x, если в этой точке она имеет конечную производную. Операция нахождения производной при этом называется дифференцированием функции.
Рассмотрим три примера, которые демонстрируют технику вычисления производной с помощью определения 6.1.1.
Пример 6.1.1.
Пусть f(x) = x. Тогда 4f = f(x + 4x) − f(x) = x + 4x − x = 4x, а следова-
тельно, |
4f |
|
4x |
|
|
f 0(x) = lim |
= lim |
= 1. |
|||
4x |
4x |
||||
4x→0 |
4x→0 |
|

Производная функции |
75 |
Пример 6.1.2.
Пусть f(x) = x2. Тогда 4f = f(x+ 4x) −f(x) = (x+ 4x)2 −x2 = 2x4x+ (4x)2,
а следовательно,
|
|
|
f 0(x) = lim |
0 |
4f |
= |
lim (2x + |
x) = 2x. |
|||||||||||||
|
|
|
|
|
|
4 |
x |
→ |
4 |
x |
|
4 |
x |
→ |
0 |
|
4 |
|
|||
Пример 6.1.3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пусть |
f(x) = |x|. Покажем, что при |
x = 0 производная этой функции не суще- |
|||||||||||||||||||
ствует. Рассмотрим приращение данной функции в точке x = 0. Легко видеть, |
|||||||||||||||||||||
÷òî |
4f |
x=0 = f(0 + 4x) − f(0) = f(4x) = |4x|. |
|||||||||||||||||||
Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x x=0 = |4x| = ( |
|
|
1, когда |
4x < 0. |
||||||||||||||||
|
|
|
f |
|
|
|
|
|
x |
|
|
|
+1, когда |
x > 0, |
|||||||
|
4 |
|
|
|
|
|
4 |
|
|
|
|
− |
|
|
|
4 |
|
||||
Последнее означает, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x → 0 |
не существует, а следо- |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
что предел этой дроби при |
|
|
|
|||||||||||||||
вательно, не существует и |
f 0(0). |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
6.2. Геометрический смысл производной
В школьном курсе планиметрии вводятся понятия секущей и касательной к окружности. Они допускают обобщение, позволяющее говорить о секущей и касательной к графику той или иной функции.
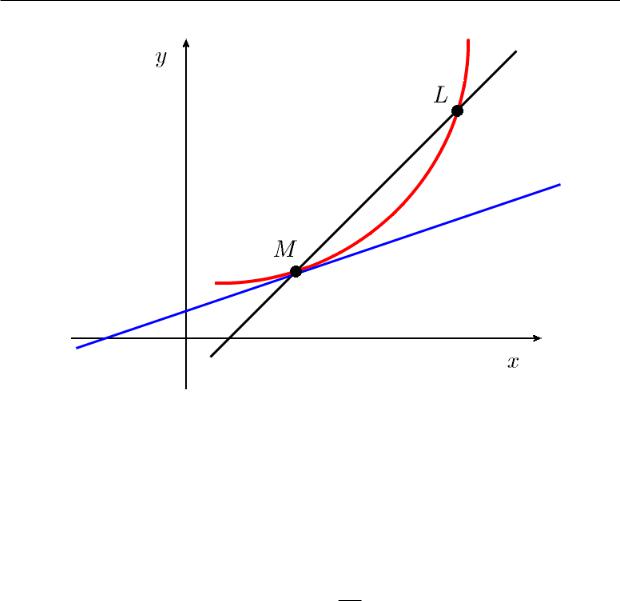
Во многих случаях касательную к кривой, проведенную в точке M, можно рассматри-
вать как предельное положение секущей ML, когда точка L, двигаясь вдоль кривой,
стремится к точке M (ñì. ðèñ. 6.2.1).
На рис. 6.2.2. показана касательная к кривой y = f(x), проведенная в точке M,
и секущая, проходящая через точки M è L. Из треугольника LMN следует, что тангенс угла наклона этой секущей к оси абсцисс находится по формуле
tg ϕ = NLNM = 44fx.
Производная функции |
76 |
Рис. 6.2.1. Секущая ML и касательная к кривой, проведенная в точке M.
Когда 4x → 0, точка L, двигаясь вдоль кривой, стремится к точке M. Ïðè ýòîì
секущая ML, меняя свой наклон к оси абсцисс, приближается к касательной к кри-
âîé y = f(x), проведенной в точке M. Это означает, что тангенс угла наклона этой касательной к оси абсцисс находится по формуле
tg α = lim 4f .
4x→0 4x
Применяя определение производной 6.1.1, приходим к выводу, что тангенс угла наклона к оси абсцисс касательной к графику функции y = f(x), проведенной в точке
с координатами (x, f(x)), совпадает со значением производной данной функции в этой точке, т. е.
tg α = f 0(x).
Эта формула и определяет геометрический смысл производной. Она позволяет сделать весьма важный вывод: чем быстрее растут или убывают значения функции при
изменении значений ее аргумента, тем больше будет абсолютная величина тангенса
угла наклона касательной. Значит, производная характеризует скорость изменения функции при изменении ее аргумента.
