5 |
Непрерывность функции |
64 |
|
|
|
Понятие непрерывности, кажущееся вполне ясным, в действительности является сложным и очень тонким. Интуитивное понятие непрерывности связано с представлением о непрерывности кривой, о непрерывности процессов, происходящих в природе. Непрерывное движение тела описывается функцией, показывающей непрерывную зависимость пути от времени. Математическое понятие непрерывности функции отражает свойство непрерывности природных, производственных процессов. Это понятие является одним из основных понятий математического анализа. Далее мы дадим математическое определение непрерывности (даже два!), определим, что такое точки разрыва и проведем их классификацию, приведем основные свойства непрерывных функций.
5.1. Приращения аргумента и функции
Пусть функция y = f(x) определена в некоторой окрестности точки x0 (ñì. îïðå-
деление 3.2.2 на стр. 21). Возьмем такое число |
4x 6= 0, чтобы значение аргумента |
x = x0 + 4x не выходило из окрестности точки |
x0. |
Определение 5.1.1.
Величина |
4x = x − x0 называется приращением аргумента в точке x0, |
а величина |
4f = f(x) − f(x0) = f(x0 + 4x) − f(x0) приращением функции |
в этой точке, соответствующим приращению аргумента 4x.
Замечание.
Приращение аргумента 4x это просто некоторая переменная величина, имею-
щая числовые значения. Значению аргумента x0 соответствует значение функ- öèè f(x0), а значению аргумента x0 + 4x соответствует значение функции
f(x0 + 4x). Разность между этими двумя значениями функции
4f = f(x0 + 4x) − f(x0)
и называется ее приращением, соответствующим приращению аргумента 4x â
точке x0.
Непрерывность функции |
65 |
Геометрический смысл этого определения показан на рис 5.1.1.
Рис. 5.1.1. Приращение аргумента и приращение функции.
5.2. Два определения непрерывности
Пусть функция y = f(x) определена в некоторой окрестности точки x0.
Определение 5.2.1.
Функция y = f(x), называется непрерывной в точке x0, если бесконечно ма-
лому приращению аргумента в этой точке соответствует бесконечно малое приращение функции, т. е.
lim 4f = 0.
4x→0
Рассмотрим примеры, иллюстрирующие это определение.
Непрерывность функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
66 |
||
Пример 5.2.1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Показать, что функция |
f(x) = x |
|
|
непрерывна в произвольной точке x0 R. |
|||||||||||||||||||||||
Применяя определение 5.2.1, получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
lim |
f = |
lim |
4 |
x = 0. |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
4 |
x 0 4 |
|
|
|
4 |
x 0 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
→ |
|
|
|
→ |
|
|
|
|
|
|
|
|
|
|
|
||||||
Утверждение доказано. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 5.2.2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Показать, что функция |
f(x) = x2 |
непрерывна в произвольной точке |
x0 R. |
||||||||||||||||||||||||
Легко видеть, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
4f = f (x0 + 4x) − f (x0) = (x0 + 4x)2 − x02 = |
|
|
|||||||||||||||||||||||
|
|
= x02 + 2x04x + (4x)2 − x02 = 2x04x + (4x)2. |
|
|
|||||||||||||||||||||||
Теперь получаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
lim |
4 |
f = |
lim |
2x |
|
4 |
x + ( |
4 |
x)2 |
= |
lim 2x |
|
4 |
x + |
lim ( |
x)2 |
= |
||||||||||
4x→0 |
|
4x→0 |
|
|
0 |
|
|
|
|
|
4x→0 |
|
|
0 |
|
4x→0 |
4 |
|
|||||||||
|
|
|
= 2 |
|
0 |
4x→0 4 |
|
|
4x→0 |
4 |
|
|
2 |
|
|
|
|
|
|||||||||
|
|
|
x |
x + |
|
|
|
= 0. |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
lim |
|
|
|
lim |
|
x |
|
|
|
|
|
||||||||
Это дает нам возможность применить определение 5.2.1. Утверждение доказано.
Определение 5.2.2.
Функция y = f(x) называется непрерывной в точке x0, если ее предел при x → x0 существует и равен значению функции в этой точке, т. е.
lim f (x) = f (x0) .
x→x0
Покажем эквивалентность этих двух определений непрерывности функции в точке. Пусть функция y = f (x) непрерывна в точке x0
lim 4f = 0.
4x→0
Непрерывность функции |
|
|
|
|
|
|
|
|
|
|
67 |
|
Поскольку |
4f = f(x0 + 4x) − f(x0) = f(x) − f(x0), |
отсюда следует, что |
||||||||||
|
lim |
f(x) |
− |
lim |
0 |
f(x |
) = 0, |
|||||
|
4 |
x |
→ |
0 |
4 |
x |
→ |
0 |
|
|
||
|
|
|
|
|
|
|
|
|
||||
а значит, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
f(x) = f(x0). |
|
||||||
|
|
|
|
4x→0 |
|
|
|
|
|
|
|
|
Последнее означает, что функция |
y = f (x) |
непрерывна в точке x0 в смысле опреде- |
||||||||||
ления 5.2.2, поскольку условие 4x → 0 |
равносильно условию x − x0 → 0, а значит, |
|||||||||||
и условию |
x → x0. |
|
|
|
|
|
|
|
|
|
|
|
Пусть теперь функция y = f (x) |
непрерывна в точке |
x0 в смысле определения 5.2.2, |
||||||||||
ò. å. |
|
|
|
|
|
|
|
|
|
|
|
|
lim f(x) = f(x0).
x→x0
Отсюда следует, что
lim (f(x) − f(x0)) = 0.
4x→0
Но тогда
lim 4f = 0,
4x→0
а значит, функция y = f (x) непрерывна в точке x0 в смысле определения 5.2.1.
5.3. Точки разрыва и их классификация
Если функция y = f(x) определена в некоторой окрестности точки x0, то ее непре-
рывность в этой точке, как легко догадаться, означает, что вблизи данной точки небольшие изменения аргумента приводят к небольшим изменениям функции.
Когда функция не является непрерывной в некоторой точке x0, говорят, что в этой точке она претерпевает разрыв. Сама точка x0 называется при этом точкой разрыва.
Пусть функция y = f(x) определена в некоторой окрестности точки x0, за исклю- чением, быть может, самой этой точки. Мы будем предполагать, что f(x) → A ïðè
x → x0 слева (x < x0) è f(x) → B ïðè x → x0 справа (x > x0). Тогда мы можем столкнуться со следующими случаями.
Непрерывность функции |
68 |
1. Числа A è B конечны, причем A 6= B. Тогда говорят, что в точке |
x0 функция |
y = f(x) претерпевает скачок.
2.Числа A è B конечны, причем A = B, но в самой точке x0 функция либо не определена, либо ее значение не совпадает с числом A. Тогда говорят, что в точке
x0 функция y = f(x) имеет устранимый разрыв. Это название объясняется тем, что в рассматриваемом случае мы можем устранить разрыв, рассматривая
новую функцию y = f0(x), которая задается следующим образом
(
f(x), åñëè x 6= x0,
f0(x) =
A, åñëè x = x0.
Она будет непрерывной в точке x0.
3. |A| = ∞ èëè |B| = ∞. Тогда говорят, что в точке x0 функция y = f(x)
претерпевает бесконечный разрыв.
Замечание.
Скачки и устранимые разрывы называются обычно разрывами первого рода, а бесконечные разрывы разрывами второго рода.
Рис. 5.3.1. Разрыв первого рода иногда чреват неприятностями.
Непрерывность функции |
69 |
Пример 5.3.1.
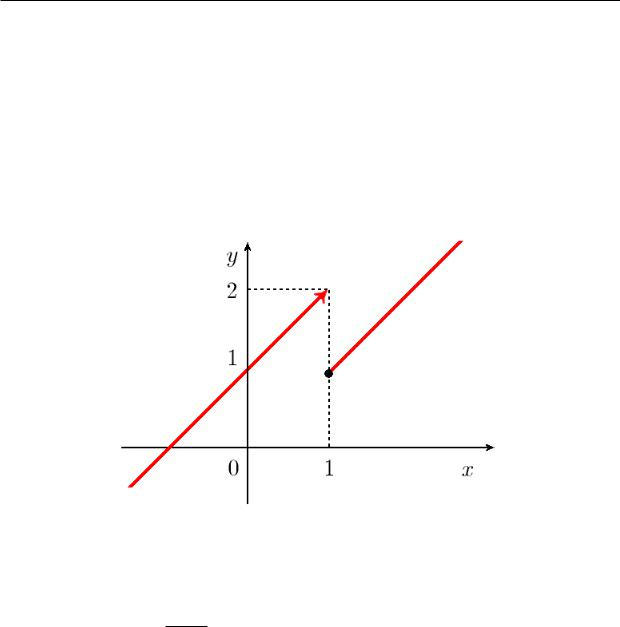
Функция, которая задается следующим правилом:
(
x,
y = f(x) =
x + 1,
åñëè
åñëè
x > 1,
x < 1,
в точке x0 = 1 претерпевает скачок. Ее график показан на рис. 5.3.2.
Рис. 5.3.2. Данная функция имеет разрыв первого рода (скачок).
Пример 5.3.2.
Функция f(x) = |
x2 − 4 |
|
x |
0 |
= 2 не определена, но f(x) |
→ |
4, независимо |
||||||
îò òîãî, êàê |
|
|
x |
− |
2 в точке |
|
|
|
|
|
|||
|
x |
стремится к |
x0 |
= 2 |
(слева или справа). Значит, в точке |
x0 |
= 2 |
||||||
|
|
|
|
|
|
|
|
||||||
данная функция имеет устранимый разрыв. |
|
|
|
|
|||||||||
Пример 5.3.3.
Функция f(x) = |
1 |
в точке x0 |
= 3 имеет разрыв второго рода, поскольку |
||||||
|
|||||||||
3 − x |
|||||||||
f(x) → ∞, |
когда |
|
слева, и |
f(x) → −∞, |
когда |
x → 3 |
справа. График |
||
|
x → 3 |
|
|
|
|||||
этой функции показан на рис. 5.3.3. Хорошо видно, что слева от точки разрыва x0 = 3 значения функции уходят на +∞, а справа на −∞.