1. Пусть m–некоторое множество пар действительных чисел , l–некоторое множество действительных чисел.

Функцией двух переменных называется правило, по которому каждой паре чисел  соответствует единственное число  , при условии, что каждое число   соответствует хотя бы одной паре  .

При этом x и y называют независимыми переменными, или аргументами, z–зависимой переменной, или функцией переменных х и у, множество М–областью определения функции,L–множеством значений, или областью изменения функции.

Обозначают: 

Если паре   соответствует число  , то пишут  , или  . Число   называют при этом частным значением функции при  .

Так как каждой паре чисел   соответствует единственная точка   плоскости Оху и обратно, каждой точке   соответствует единственная пара чисел  , то функцию двух переменных можно рассматривать как функцию точки и писать   вместо  .

В этом случае областью определения функции является некоторое множество точек плоскости Оху.

Если значение   принять за аппликату соответствующей точки   пространства, то множество таких точек образуют, вообще говоря, некоторую поверхность, которую называют графиком функции   (рис.15).

Если функция задана с помощью аналитического выражения, то областью ее определения считают множество всех таких точек плоскости Oxy, для которых это выражение имеет смысл и дает действительные значения функции.

Например, функция z=2x+3y–1 определена на всей плоскости Oxy, графиком ее является п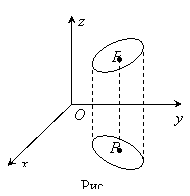 лоскость; функция  определена при  , то есть –внутри круга радиуса r=1 с центром в начале координат, график этой функции–полусфера радиуса R=1.

Определение функции двух переменных легко обобщить на случай большего числа переменных. Так, функцией трех переменных называется правило, по которому каждой тройке действительных чисел   соответствует единственное действительное число  , при условии, что каждое число  соответствует хотя бы одной тройке .

Обозначают:  ,  .

Областью определения функции трех переменных является некоторое множество точек в пространстве. Саму функцию трех переменных изобразить с помощью графика в пространстве невозможно.

2.

3. Пусть    -- внутренняя точка области   , и в области   задана функция   . Рассмотрим ограничение функции   на прямую   , проходящую через точку   параллельно оси  . Эта прямая задаётся условиями   при   ; переменная   может при этом произвольно меняться. Поэтому для рассматриваемого ограничения   имеется естественная параметризация, смысл которой в том, что "замораживаются" все переменные, от которых зависит   , кроме   :

Получили функцию одного переменного   , как параметризацию ограничения с помощью параметра   .

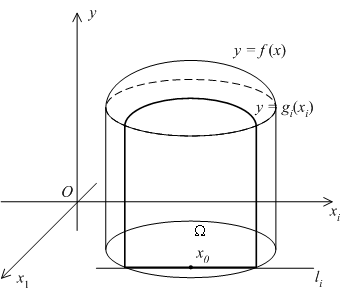
Рис.7.12.

Функция   может иметь производную в точке   , равную некоторому числу   . Это число называют частной производной функции   по переменной   , вычисленной в точке   . Эта частная производная обозначается   или   .

Сразу же заметим, что значения частных производных от функции   в точке   , вычисленные по разным переменным   и   , могут быть различными, так что обозначение типа   , без указания переменной, по которой вычислена частная производная, не имеет смысла: в обозначении обязательно нужно указывать переменную, по которой мы дифференцируем.

Итак, чтобы вычислить частную производную от функции   по некоторой переменной   , нужно фиксировать значения всех переменных, кроме   (то есть временно считать их постоянными), а затем по обычным правилам вычисления производных найти производную по этой единственной переменной   . Теперь ясно, что для вычисления частных производных никаких новых правил дифференцирования вдобавок к тем, что известны нам для функций одной переменной, не потребуется, ведь при вычислении частной производной мы считаем, что может изменяться только одна переменная.

Считая точку   , в которой вычисляется значение частной производной   , переменной точкой области   и предполагая, что во всех точках   эта производная существует, мы получаем, что частная производная    -- это функция, заданная в области   (или в её части, если производная существует не везде в   ).

Поскольку частную производную функции   можно вычислять по каждой из   переменных   , то функция   имеет   частных производных

Эти частные производные, вообще говоря, -- различные функции. Их называют также частными производными первого порядка от функции   . Итак, функция   переменных имеет   частных производных первого порядка.

4.

5. Обобщением определенного интеграла на случай функций двух переменных является так называемый двойной интеграл.

Пусть в замкнутой области D плоскости Оху задана непрерывная функция z=ƒ(х;у). Разобьем область D на n «элементарных областей» площади которых обозначим через ΔSi, а диаметры (наибольшее расстояние между точками области) - через di

В каждой области Di выберем произвольную точку Mi(xi;yi), умножим значение ƒ(хi;уi) функции в этой точке на ΔSi и составим сумму всех таких произведений:

Эта сумма называется интегральной суммой функции ƒ(х;у) в области D.

Рассмотрим предел интегральной суммы (7.1), когда n стремится к бесконечности таким образом, что maxdi -> 0. Если этот предел существует и не зависит ни от способа разбиения области D на части, ни от выбора точек в них, то он называется двойным интегралом от функции ƒ(х;у) по области D и обозначается

Таким образом, двойной интеграл определяется равенством

В этом случае функция ƒ(х;у) называется интегрируемой в области D; D - область интегрирования; х и у - переменные интегрирования; dxdy (или dS) - элемент площади.

Для всякой ли функции ƒ(х;у) существует двойной интеграл? На этот вопрос отвечает следующая теорема, которую мы приведем здесь без доказательства.

Теорема 7.1 (достаточное условие интегрируемости функции). Если функция z=ƒ(х; у) непрерывна в замкнутой области D, то она интегрируема в этой области.

Замечания.

1. Далее будем рассматривать только функции, непрерывные в области интегрирования, хотя двойной интеграл может существовать не только для непрерывных функций.

2. Из определения двойного интеграла следует, что для интегрируемой в области D функции предел интегральных сумм существует и не зависит от способа разбиения области. Таким образом, мы можем разбивать область D на площадки прямыми, параллельными координатным осям При этом равенство (7.2) можно записать в виде

6. Основные свойства двойного интеграла

Можно заметить, что процесс построения интеграла в области D дословно повторяет уже знакомую нам процедуру определения интеграла функции одной переменной на отрезке (см. Часть 1, п. 35). Аналогичны и свойства этих интегралов и их доказательства. Поэтому перечислимосновные свойства двойного интеграла, считая подынтегральные функции интегрируемыми.

1.

2.

3Если область D разбить линией на две област и D1 и D2 такие, что а пересечение D1 и D состоит лишь из линии, их разделяющей (см. рис. 6), то

4.Если в области D имеет место неравенство ƒ(х;у) >=0, то и Если в области D функции ƒ(х; у) и j(х; у) удовлетворяютнеравенству

5.

6. Если функция ƒ(х; у) непрерывна в замкнутой области D, площадь которой S, то где m и М - соответственно наименьшее и наибольшее значения подынтегральной функции в области D.

7. Если функция ƒ(х;у) непрерывна в замкнутой области D, площадь которой S, то в этой области существует такая точка (хо;уо), что

S.

Величину называют средним значением функции ƒ(х;у) в области D.

7) Вычисление двойного интеграла в декартовых координатах

Покажем, что вычисление двойного интеграла сводится к последовательному вычислению двух определенных интегралов.

Пусть требуется вычислить двойной интеграл где функция ƒ(х;у)>=0 непрерывна в области D. Тогда, как это было показано в п. 7.2, двойной интеграл выражает объем цилиндрического тела, ограниченного сверху поверхностью z=ƒ(х;у). Найдем этот объем, используя метод параллельных сечений. Ранее (см. Часть 1, (41.6)) было показано, что

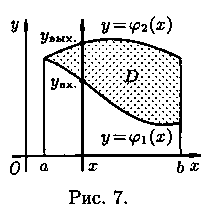
где S(x) - площадь сечения плоскостью, перпендикулярной оси Ох, a x=a,x=b - уравнения плоскостей, ограничивающих данное тело.

Положим сначала, что область D представляет собой криволинейную трапецию, ограниченную прямыми х=а и х=b и кривыми у=j1(x) и у=j2(х), причем функции j1(x) и j2(х) непрерывны и таковы, что j1(x) ≤ j2(х) для всех х є [а;b] (см. рис. 7). Такая область называется правильной в направлении оси Оу: любая прямая, параллельная оси Оу, пересекает границу области не более чем в двух точках.

Построим сечение цилиндрического тела плоскостью, перпендикулярной оси Ох: х =const, где х є [а; b].

В сечении получим криволинейную трапецию ABCD, ограниченную линиями z=ƒ(х;у), где х=const, z=0, у=j1(x) и у=j2(х) (см. рис. 8). Площадь S(х) этой трапеции находим с помощью определенного интеграла

Теперь, согласно методу параллельных сечений, искомый объем цилиндрического тела может быть найдентак:

С другой стороны, в п. 7.2 было доказано, что объем цилиндрического тела определяется как двойной интеграл от функции ƒ(х;у) >=0 по области D. Следовательно,

Это равенство обычно записывается в виде

Формула (7.7) представляет собой способ вычисления двойного интеграла в декартовых координатах. Правую часть формулы (7.7) называют двукратным (или повторным) интегралом от функции ƒ(х; у) по области D.

8) При этом называется внутренним интегралом.

Для вычисления двукратного интеграла сначала берем внутренний интеграл, считая х постоянным, затем берем внешний интеграл, т. е. результат первого интегрирования интегрируем по х в пределах от а до b.

Если же область D ограничена прямыми y=c и y=d(c<d), кривыми x=Ψ1(у)и х=Ψ2(у)> причем Ψ1(у)≤Ψ2(у) для всех у є [с;d], т. е. область D - правильная в направлении оси Ох, то, рассекая тело плоскостью у=const, аналогично получим:

Здесь, при вычислении внутреннего интеграла, считаем у постоянным.

Замечания.

1. Формулы (7.7) и (7.8) справедливы и в случае, когда ƒ(х;у)<0, (x;y) e D.

2. Если область D правильная в обоих направлениях, то двойной интеграл можно вычислять как по формуле (7.7), так и по формуле (7.8).

3. Если область D не является правильной ни «по х», ни «по у», то для сведения двойного интеграла к повторным ее следует разбить на части, правильные в направлении оси Ох или оси Оу.

4. Полезно помнить, что внешние пределы в двукратном интеграле всегда постоянны, а внутренние, как правило, переменные.

9) уравнения связанные независимыми переменными искомую функцию и ее производные называются дифферинциальными если искомая функция зависит от одной переменной называемой обыкновенной в противном случае уравнение в частных производных

Основные понятия

При решении различных задач математики, физики, химии и других наук часто пользуются математическими моделями в виде уравнений, связывающих независимую переменцую, искомую функцию и ее производные. Такие уравнения называются диффepeнциaльными (термин принадлежит Г.Лейбницу, 1676 г.). Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество

Так, решением уравнения y'=ƒ(х) является функция y=F(x) - первообразная для функции ƒ(x),

Рассмотрим некоторые общие сведения о дифференциальных уравнениях (ДУ).

Если искомая (неизвестная) функция зависит от одной переменной, то ДУ называют обыкновенным; в противном случае - ДУ в частных производных. Далее будем рассматривать только обыкновенные ДУ.

Наивысший порядок производной, входящей в ДУ, называется порядком этого уравнения.

Например, уравнение y'''- Зy''+2у=0 - обыкновенное ДУ третьего порядка, а уравнение х2y'+5хy=y2 - первого порядка; у • z'x=х • z'y - ДУ в частных производных первого порядка.

Процесс отыскания решения ДУ называется его интегрированием, а график решения ДУ - интегральной кривой.

10) Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество.

Так, решением уравнения y'=ƒ(х) является функция y=F(x) - первообразная для функции ƒ(x)_,

Общим решением ДУ первого порядка называется функция y=(х;с), содержащая одну произвольную постоянную и удовлетворяющая условиям:

1. Функция (х; с) является решением ДУ при каждом фиксированном значении с.

2. Каково бы ни было начальное условие (2.4), можно найти такое значение постоянной с=с_о, что функция y=(х; с_о) удовлетворяет данному начальному условию.

Чacтным решением ДУ первого порядка называется любая функция у= (х;с_о), полученная из общего решения у=(х;с) при конкретном значении постоянной с=с_о.

Если общее решение ДУ найдено в неявном виде, т. е. в виде уравнения Ф(х;y;с) =0, то такое решение называется частным интегралом ДУ. Уравнение Ф(х;y;с_о) =0 в этом случае называется частным интегралом уравнения.

С геометрической точки зрения y=(х;с) есть семейство интегральных кривых на плоскости Охy; частное решение у=ф(х;с_о)-одна кривая из этого семейства, проходящая через точку (х_о;y_о).

11) Дифференциальное уравнение первого порядка в общем случае можно записать в виде

F(x;y;y')=0. (2.1)

Уравнение связывает независимую переменную х, искомую функцию y и ее производную y'. Если уравнение (2.1) можно разрешить относительно y', то его записывают в виде

У'=ƒ(х;у) (2.2)

и называют ДУ первого порядка, разрешенным относительно производной. Мы в основном будем рассматривать эту форму записи ДУ.

Уравнение (2.2) устанавливает связь (зависимость) между координатами точки (х;y) и угловым коэффициентом y' касательной к интегральной кривой, проходящей через эту точку. Следовательно, ДУ y'=ƒ(х; y) дает совокупность направлений (поле направлений) на плоскости Охy. Таково геометрическое истолкование ДУ первого порядка.

Кривая, во всех точках которой направление поля одинаково, называется изоклиной. Изоклинами можно пользоваться для приближенного построения интегральных кривых. Уравнение изоклины можно получить, если положить y'=с, т.е. ƒ(x;y)=с.

11)Общим решением ДУ первого порядка называется функция y=j(х;с), содержащая одну произвольную постоянную и удовлетворяющая условиям:

1. Функция j(х; с) является решением ДУ при каждом фиксированном значении с.

2. Каково бы ни было начальное условие (2.4), можно найти такое значение постоянной с=со, что функция y=j(х; со) удовлетворяет данному начальному условию.

Чacтным решением ДУ первого порядка называется любая функция у= j(х;со), полученная из общего решения у=j(х;с) при конкретном значении постоянной с=со.

Если общее решение ДУ найдено в неявном виде, т. е. в виде уравнения Ф(х;y;с) =0, то такое решение называется частным интегралом ДУ. Уравнение Ф(х;y;со) =0 в этом случае называется частным интегралом уравнения

12)С геометрической точки зрения y=j(х;с) есть семейство интегральных кривых на плоскости Охy; частное решение у=ф(х;со)-одна кривая из этого семейства, проходящая через точку (хо;yо).

Задача отыскания решения ДУ первого порядка (2.3), удовлетворяю-щего заданному начальному условию (2.4), называется задачей Коши.

Теорема 2.1 (существования и единственности решения задачи Коши). Если в уравнении (2.2) функция ƒ(x;y) и ее частная производная ƒ'y(x;y) непрерывны в некоторой области D, содержащей точку (хо;yо), то существует единственное решение у=j(х) этого уравнения, удовлетворяющее начальному условию (2.4).

Геометрический смысл теоремы состоит в том, что при выполнении ее условий существует единственная интегральная кривая ДУ, проходящая через точку (xо;yо).

13)

14) Уравнения с разделяющимися переменными

Наиболее простым ДУ первого порядка является, уравнение виДа

P(x)•dz+Q(y)•dy=0. (2.5)

В нем одно слагаемое зависит только от х, а другое - от у. Иногда такие ДУ называют уравнениями с разделенными переменными. Проинтегрировав почленно это уравнение, получаем:

- его общий интеграл.

Пример 2.2. Найти общий интеграл уравнения х•dx+у•dy=0.

Решение: Данное уравнение есть ДУ с разделенными переменными. Поэтому Обозначим с/2=c1. Тогда х2-y2=с - общий интеграл ДУ.

Более общий случай описывают уравнения с разделяющимися переменными, которые имеют вид

Особенность уравнения (2.6) в том, что коэффициенты при dx и dY представляют собой произведения двух функций (чисел), одна из которых зависит только от х, другая - только от у.

Уравнение (2.6) легко сводится к уравнению (2.5) путем почленного деления его на Q1(у)•Р2(х)≠0.

15)Замечания.

1. При проведении почленного деления ДУ на Q1(y)•Р2(х) могут быть потеряны некоторые решения. Поэтому следует отдельно решить уравнение Q1(у)•Р2(х)=0 и установить те решения ДУ, которые не могут быть получены из общего решения, - особые решения.

2. Уравнение y'=ƒ1(х)•ƒ2(y) также сводится к уравнению с разделенными переменными. Для этого достаточно положить и разделить переменные.

3. Уравнение y'=ƒ(ах+by+с), где а,b,с - числа, путем замены ах+by+с=u сводится к ДУ с разделяющимися переменными. Дифференцируя по х, получаем:

Данное уравнение принимает вид откуда следует

Интегрируя это уравнение и заменяя u на ах+by+с, получим общий интеграл исходного уравнения.

16) К уравнению с разделяющимися переменными приводятся однородные ДУ первого порядка.

Функция ƒ(x;y) называется однородной функцией N-го поpядкa (измерения), если при умножении каждого ее аргумента на произвольный множитель λ вся функция умножится на AN, т. е.

Например, функция ƒ(x;у)=х2-2ху есть однородная функция вто-рого порядка, поскольку

Дифференциальное уравнение

У'=ƒ(х; у) (2.7)

называется однородным, если функция ƒ(х;у) есть однородная функция нулевого порядка.

Покажем, что однородное ДУ (2.7) можно записать в виде

Если ƒ(x;у) - однородная функция нулевого порядка, то, по определению, Положив получаем:

однородное уравнение (2.8) преобразуется в уравнение с разделяющимися переменными при помощи замены переменной (подстановки)

Действительно, подставив у=uх и y'=u'x+u в уравнение (2.8), получаем уравнение с разделяющимися переменными. Найдя его общее решение (или общий интеграл), следует заменить в нем u на . Получим общее решение (интеграл) исходного уравнения.

Однородное уравнение часто задается в дифференциальной форме:

ДУ (2.10) будет однородным, если Р(х;у) и Q(x;у) - однородные функции одинакового порядка.

Переписав уравнение (2.10) в виде и применив в правой части рассмотренное выше преобразование, получим уравнение

При интегрировании уравнений вида (2.10) нет необходимости предварительно приводить их (но можно) к виду (2.8): подстановка (2.9) сразу преобразует уравнение (2.10) в уравнение с разделяющимися переменными.

Пример 2.6. Найти общий интеграл уравнения

Решение: Данное уравнение однородное, т. к. функции Р(х;у)=х2-у2 и Q(x;у)=2ху - однородные функции второго порядка.

Положим у=u • х. Тогда dy=х • du+u • dx. Подставляем в исходное уравнение:

последнее - уравнение с разделяющимися переменными. Делим переменные

и интегрируем

Обозначим Тогда

Заменяя u на получаем: х2+у2=сх - общий интеграл исходного уравнения.

Отметим, что данное уравнение можно было сначала привести к виду (2.8):

Затем положить у=u • х, тогда y'=u'x+u и т. д.

Замечание. Уравнение вида где а, b, с, a1, b1, c1 - числа, приводится к однородному или с разделяющимися переменными. Для этого вводят новые переменные u и v, положив х=u+а, y=v+β, где а и β - числа. Их подбирают так, чтобы уравнение стало однородным.