
- •1.1. Как пользоваться этим учебником
- •1.2. О курсе высшей математики
- •1.3. Биология, почвоведение и математика
- •2. Базовые понятия
- •2.1. Множества
- •2.2. Высказывания
- •2.3. Кванторы
- •2.4. Системы координат
- •2.5. Абсолютная величина числа
- •3. Функция
- •3.1. Величины постоянные и переменные
- •3.2. Определение функции
- •3.3 Способы задания функции
- •3.5. Периодическая функция
- •3.6. Ограниченная функция
- •3.7. Суперпозиция функций
- •3.8. Обратная функция
- •3.9. Неявная функция
- •3.10. Однозначная и многозначная функция
- •3.11. Рекомендации
- •3.12. Вопросы для самоконтроля
- •4. Предел функции
- •4.1. Определение предела функции
- •4.3. Бесконечно малая величина
- •4.4. Бесконечно большая величина
- •4.5. Свойства пределов
- •4.6. Неопределенность вида 0/0
- •4.7. Неопределенность вида ∞/∞
- •4.9. Первый замечательный предел
- •4.10. Второй замечательный предел
- •4.11. Основные теоремы о пределах
- •4.12. Рекомендации
- •4.13. Вопросы для самоконтроля
- •5.1. Приращения аргумента и функции
- •5.2. Два определения непрерывности
- •5.3. Точки разрыва и их классификация
- •5.4. Свойства непрерывных функций
- •5.5 Рекомендации
- •5.6. вопросы для самоконтроля
- •6. Производная функции
- •6.1. Определение производной
- •6.2. Геометрический смысл производной
- •6.3. Механический смысл производной
- •6.4. Основные теоремы о производных
- •6.5. Производные элементарных функций
- •6.6 Сводка формул
- •6.7. Примеры на вычисление производной
- •6.8. Производные высших порядков
- •6.9. Рекомендации
- •6.10. Вопросы для самоконтроля
- •7. Приложения производной
- •7.1. Возрастание и убывание функции
- •7.2. Экстремумы функции
- •7.3. Наибольшее и наименьшее значения функции на промежутке
- •7.4. График функции
- •7.5. Уравнение касательной
- •7.6. Приближенные решения уравнений
- •7.7. Правила Лопиталя
- •7.8. Рекомендации
- •7.9. Вопросы для самоконтроля
- •8. Дифференциал функции
- •8.1. Определение дифференциала функции
- •8.2. Свойства дифференциала
- •8.3. Геометрический смысл дифференциала
- •8.4. Рекомендации
- •8.5. Вопросы для самоконтроля
- •9. Примеры контрольных работ
- •11. Формулы
- •11.1. Основные свойства степени
- •11.2. формулы сокращенного умножения
- •11.3. Квадратное уравнение
- •11.4. Разложение квадратного трехчлена на множители
- •11.5. Основные свойства логарифмов
- •11.6. Тригонометрические формулы
- •12 Литература
- •13. Об авторах этого учебника
- •14. Предметный указатель
Приложения производной |
123 |
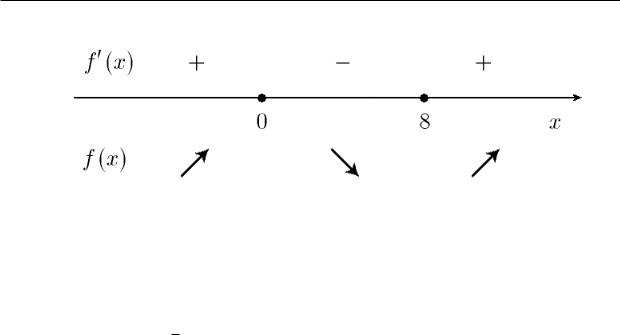
Хорошо видно, что при переходе через каждую из двух критических точек производная меняет знак. Применяя первое достаточное условие экстремума (теорему 7.2.2), заключаем, что рассматриваемая функция достигает своего максимума
ïðè x = 0, а минимума при x = 8. В точках экстремума fmax = f(0) = 0
4 è fmin = f(8) = −3.
7.3. Наибольшее и наименьшее значения функции на промежутке
В общем случае для непрерывной функции справедливы следующие утверждения.
1. Если непрерывная функция y = f(x) задана на замкнутом промежутке [a, b],
то она обязательно достигает как своего наименьшего, так и своего наибольшего значений, причем происходит это либо в точке экстремума, либо на конце промежутка.
2. Если же функция задана на открытом промежутке (a, b), то она может достигать, а может и не достигать своего наименьшего и своего наибольшего значений.
Чтобы прояснить суть рассматриваемой проблемы, решим несколько простых примеров.
Пример 7.3.1.
Пусть функция f(x) = 2x задана на замкнутом промежутке [1, 3]. Эта функция
является возрастающей, т. к. ее производная f 0(x) = 2 положительна. Поэтому
f(1) 6 f(x) 6 f(3), значит, данная функция достигает своего наименьшего зна-
чения на левом конце промежутка [1, 3], а наибольшего на его правом конце,
ò. å. fíàèì = f(1) = 2, à fíàèá = f(3) = 6.

Приложения производной |
124 |
Пример 7.3.2.
Ситуация кардинально меняется, если функция f(x) = 2x задана на открытом
промежутке (1, 3). В этом случае для любого значения x (1, 3) выполняется
неравенство 2 < f(x) < 6, а значит, ни наименьшего, ни наибольшего значений
данная функция на открытом промежутке (1, 3) достичь не может. Ее значения
подходят сколь угодно близко к числу 2, когда аргумент x приближается к ле-
вому концу промежутка (1, 3), но достичь этого числа они не могут. Точно такая же ситуация имеет место и на правом конце данного промежутка.
Пример 7.3.3.
Пусть функция f(x) = x2 задана на замкнутом промежутке [−1, 1]. Легко убедиться, что она достигает своего наименьшего значения в точке минимума: fíàèì = f(0) = 0. А вот своего наибольшего значения она достигает на обоих
концах отрезка: fíàèá = f(−1) = f(1) = 1.
Пример 7.3.4.
Если же функция f(x) = x2 задана на открытом промежутке (−1, 1), то своего
наименьшего значения она достигает в точке минимума: fíàèì = f(0) = 0, но своего наибольшего значения она достичь не может.
Пример 7.3.5.
Пусть функция f(x) = |
2 |
(0, 1). Легко про- |
|
x |
|||
|
задана на открытом промежутке |
||
верить, что она там непрерывна и монотонно убывает, но ни наименьшего, ни |
|||
наибольшего значений на этом промежутке данная функция не достигает. Значе- ния f(x) стремятся к 2, когда x приближается к правому концу промежутка
(0, 1), но никогда не достигают этого значения. Если же x приближается к левому концу промежутка (0, 1), то значения функции неограниченно растут.
На практике для отыскания наибольшего и наименьшего значений непрерывной функции y = f(x) на замкнутом промежутке [a, b] удобно придерживаться следующего
алгоритма, основанного на том, что мы просто перебираем все значения аргумента, в которых функция может достигать своего наибольшего и своего наименьшего значе- ний.

Приложения производной |
125 |
1.Ищем все критические точки функции y = f(x), т. е. те значения ее аргумен-
та, в которых производная данной функции f 0(x) обращается в ноль или не существует.
2.Среди найденных критических точек отбираем только те, которые принадлежат промежутку [a, b]. Остальные критические точки отбрасываем.
3.Находим значения функции f(x) во всех отобранных точках, а также ее значения
f(a) è f(b) на концах отрезка. Самое большое и самое маленькое из найденных чисел и являются соответственно наибольшим и наименьшим значениями данной функции на промежутке [a, b].
Пример 7.3.6.
Пусть f(x) = 3x4 + 4x3 + 1. Требуется найти наибольшее и наименьшее значения
этой непрерывной функции на отрезке Сначала ищем критические точки
данной функции. Для этого найдем ее производную f 0(x) = 12x3 + 12x2. Она обращается в ноль в точках x1 = 0 è x2 = −1. Обе критические точки при-
надлежат отрезку [−2, 1]. Функции в этих точках имеет следующие значения:
f(0) = 1, f(−1) = 0. Найдем значения функции на концах отрезка: f(−2) = 17, f(1) = 8. Выбирая из этих чисел самое большое и самое маленькое, получаем
fíàèá = f(−2) = 17, fíàèì = f(−1) = 0.
Пример 7.3.7.
Требуется найти наибольшее и наименьшее значения функции
√
x x f(x) = 8 − 3√x
на интервале (10, 18). Эта функция не определена при x < 0 и имеет разрыв
второго рода при x = 64/9, но на интервале |
(10, 18) она определена и непрерыв- |
||||||||
на. Ее производная |
√ |
|
|
− |
√ |
|
|
|
|
f 0(x) = |
3 x(4 |
|
|
x) |
. |
||||
|
|
|
|
|
|||||
|
|
|
√ |
|
|
|
|||
|
|
|
x) |
2 |
|
||||
|
(8 − 3 |
|
|
|
|||||
Рассматриваемая функция на данном интервале имеет одну критическую точку x = 16, в которой f 0(x) = 0. При переходе через эту точку f 0(x) меняет знак с
плюса на минус, значит, при x = 16 рассматриваемая функция имеет локальный максимум, который и является ее наибольшим значением fíàèá = fmax = f(16) =
−16 на интервале (10, 18). Своего наименьшего значения на интервале (10, 18) эта функция не достигает, поскольку данный промежуток является открытым.

Приложения производной |
126 |
7.4. График функции
Умение строить графики функций, заданных аналитически, является весьма востребованным не только в учебном процессе, но и во многих сферах профессиональной деятельности тех, кто занимается научной или инженерной работой. Построение эскиза графика какой-либо функции нередко позволяет выявить те или иные особенности ее поведения, которые трудно, а иногда и невозможно, обнаружить, изучая лишь формулу, задающую данную функцию в аналитическом виде.
При рисовании эскиза графика функции соблюдать масштабы не требуется. Нужно лишь, чтобы рисунок правильно отражал все характерные особенности поведения функции.
В простейших случаях для того, чтобы нарисовать график функции, не требуется проводить полное исследование ее поведения. Такая ситуация возникает, когда рассматриваемая функция получается с помощью простейших преобразований каких-либо функций, графики которых уже известны, например, элементарных функций. Перечислим простейшие из таких преобразований.
1.График функции y = f(x)+a получается из графика функции y = f(x) сдвигом (параллельным переносом) на |a| единиц вдоль оси ординат. Если a > 0, то график сдвигается вверх, а если a < 0, òî âíèç.
2.График функции y = f(x+b) получается из графика функции y = f(x) сдвигом
|
(параллельным переносом) на |
|b | единиц вдоль оси абсцисс. Если |
b > 0, |
òî |
|
|
график сдвигается влево, а если b < 0, то вправо. |
|
|
|
|
3. |
График функции y = kf(x) |
получается из графика функции |
y = f(x) |
ïðè |
|
|
k > 0 растяжением или сжатием в k раз вдоль оси ординат. Если |
k > 1, |
òî |
||
|
график растягивается, а если |
0 < k < 1, то сжимается. |
|
|
|
4. |
График функции y = f(mx) |
получается из графика функции |
y = f(x) |
ïðè |
|
|
m > 0 растяжением или сжатием в m раз вдоль оси абсцисс. Если |
m > 1, òî |
|||
|
график сжимается, а если 0 < m < 1, то растягивается. |
|
|
|
|
5.График функции y = −f(x) получается из графика функции y = f(x) зеркальным отражением относительно оси абсцисс.
6.График функции y = f(−x) получается из графика функции y = f(x) зеркальным отражением относительно оси ординат.
Приложения производной |
127 |
7.График функции y = |f(x)| получается из графика функции y = f(x) зеркальным отражением относительно оси абсцисс тех его частей, которые лежат ниже этой оси. Те части графика функции y = f(x), которые лежат выше оси абсцисс, сохраняются.
8.График функции y = f(|x|) получается из графика функции y = f(x) зеркальным отражением относительно оси ординат тех его частей, которые лежат справа от этой оси. Те части графика функции y = f(x), которые лежат слева от оси ординат, отбрасываются.
Проверить правильность этих утверждений, как мы надеемся, читатели смогут самостоятельно (обычно эти вопросы разъясняются в школьном курсе элементарной математики), поэтому мы ограничимся лишь рассмотрением двух примеров их использования.
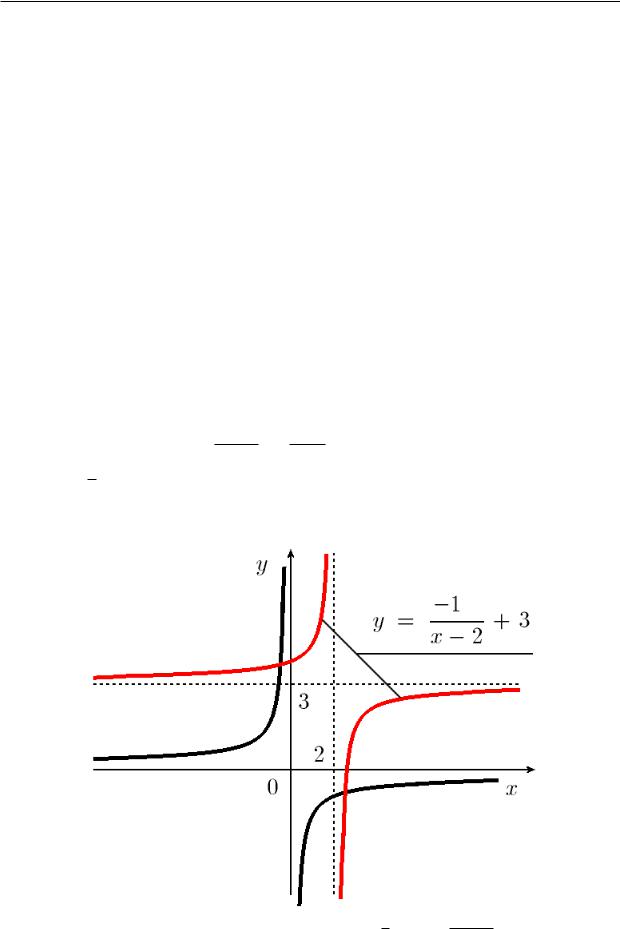
Пример. 7.4.1
График функции y = |
3x − 7 |
= |
−1 |
|
+ 3 получается из графика гиперболы |
x − 2 |
x − |
|
|||
|
|
2 |
|||
y = −x1 сдвигом вдоль оси абсцисс на 2 единицы вправо и сдвигом вдоль оси ординат на 3 единицы вверх.
Рис. 7.4.1. Графики гипербол y = −x1 è y = 3xx−−27.

Приложения производной |
128 |
|
Пример. 7.4.2 |
|
|
График функции |
y = x2 − 8x + 14 = (x − 4)2 − 2 |
получается из графика па- |
раболы y = x2 |
сдвигом вдоль оси абсцисс на 4 единицы вправо и сдвигом |
|
вдоль оси ординат на 2 единицы вниз. Чтобы получить из него график функции y = |x2 − 8x + 14| , нужно отразить относительно оси абсцисс те его части, которые лежат ниже этой оси.
Рис. 7.4.2. Графики функций y = x2 − 8x + 14 (слева) и y = |x2 − 8x + 14| (справа).
В более сложных случаях для построения графика функции y = f(x) приходится про-
водить ее исследование. Порядок выполнения пунктов такого исследования не слишком важен, но обычно мы рекомендуем проводить его в следующей последовательности.
1.Найти область определения функции.
2.Найти точки пересечения графика с осями координат.
3.Найти интервалы знакопостоянства функции промежутки оси абсцисс, на ко-
торых f(x) > 0, и промежутки, на которых f(x) < 0.
4.Установить наличие симметрии графика относительно оси ординат (она имеется у четной функции) и относительно начала координат (она есть у нечетной функции). Проверить наличие периодичности.
5.Найти интервалы монотонности функции промежутки возрастания и промежутки убывания функции.
6.Найти экстремумы функции и определить их вид.
7.Исследовать поведение функции в окрестности граничных точек области определения.

Приложения производной |
129 |
8.Найти асимптоты функции.
9.Построить график функции.
Во многих случаях для построения графика не требуется проводить полное исследование функции, вполне достаточно ограничиться отдельными его пунктами. Отметим также, что некоторые пункты данного исследования может быть довольно трудно (а иногда и невозможно) реализовать на практике. Так, скажем, отыскание точки пере-
сечения графика функции y = f(x) с осью ординат представляет собой очень простую
задачу: нужно взять x = 0 (если, разумеется, область определения функции содер-
жит ноль) и найти f(0). А вот для отыскания точек пересечения с осью абсцисс нужно
решить уравнение f(x) = 0, что не всегда возможно.
Мы впервые столкнулись здесь с термином "асимптота". Поясним его смысл.
Определение 7.4.1.
Асимптотой кривой y = f(x) называется прямая, к которой неограничен-
но приближается (подходит сколь угодно близко) точка кривой при ее удалении
вдоль кривой в бесконечность.
Замечание.
Асимптоты играют важную роль не только в математическом анализе, но и в различных прикладных научных исследованиях. Тот факт, что кривая, отражающая определенные закономерности в той или иной предметной области, при определенных условиях подходит сколь угодно близко к некоторой прямой, обычно заставляет исследователя задуматься о причинах этого явления. Нередко это свидетельствует об обнаружении нового научного факта, а иногда даже служит толч- ком, приводящим к открытию.
Асимптоты подразделяются на вертикальные, горизонтальные и наклонные.
Вертикальная асимптота кривой y = f(x) существует, если хотя бы одно из предель-
x→a+0 |
x→a−0 |
+∞ |
èëè |
−∞ |
ных значений lim f(x) èëè |
lim f(x) равно |
|
. Здесь a конечная ве- |
личина. В первом случае кривая приближается к асимптоте справа, во втором слева. Примером такой функции может служить гипербола y = 1/x, вертикальной асимпто-
той которой является ось ординат. Это типичная ситуация: вертикальные асимптоты нередко обнаруживаются, если рассмотреть значения аргумента, при которых знаменатель функции обращается в ноль. Заметим, что кривая, вообще говоря, может иметь

Приложения производной |
|
|
130 |
любое количество вертикальных асимптот. Так, скажем, кривая |
y = tg x имеет беско- |
||
нечно много таких асимптот, пересекающих ось абсцисс в точках |
x = π/2 + πn, n Z. |
||
Горизонтальная асимптота |
y = b кривой |
y = f(x) существует, если хотя бы одно |
|
из предельных значений |
lim f(x) = b èëè lim f(x) = b. Здесь b конечная ве- |
||
x→+∞ |
x→−∞ |
|
|
личина. Примером и здесь является гипербола y = 1/x, горизонтальной асимптотой
которой является ось абсцисс. Отметим, что существование у кривой двух различных горизонтальных асимптот также ничему не противоречит: точка кривой может при-
ближаться к одной из них, когда x → +∞, а к другой, когда x → −∞.
Наклонная асимптота y = kx + b кривой y = f(x) существует, если реализуется по крайней мере один из двух следующих случаев.
1. Существуют конечные пределы
k = lim f(x)
x→+∞ x è
2. Существуют конечные пределы
k = lim f(x)
x→−∞ x è
b = lim [f(x) − kx].
x→+∞
b = lim [f(x) − kx].
x→−∞
В первом из них точка кривой приближается к асимптоте, когда x → +∞, âî âòî-
ром, когда x → −∞. Подчеркнем, что одновременно реализоваться могут и оба этих
случая, причем асимптоты, к которым приближаются точки кривой, когда x → +∞
è x → −∞ могут совпадать, а могут оказаться и различными.
Рис. 7.4.3. Здесь кривая приближается к наклонной асимптоте, когда x → +∞.

Приложения производной |
131 |
Замечание.
Нетрудно заметить, что горизонтальная асимптота является частным случаем наклонной асимптоты с нулевым угловым коэффициентом k.
Пример 7.4.3.
Требуется найти асимптоты кривой
y= 2x2 + x. x + 1
1. Знаменатель этой функции обращается в ноль, когда x = −1. Убеждаясь,
x→−1+0 |
f(x) |
= +∞ |
x→−1−0 |
= −∞ |
, приходим к выводу, что |
÷òî lim |
|
è lim f(x) |
|
кривая имеет вертикальную асимптоту, которая пересекает ось абсцисс при x = −1. Отсюда следует, что одна ветвь графика данной функции уходит на
+∞, когда x приближается к значению −1 справа, а другая на −∞,
когда x приближается к −1 слева.
2.Горизонтальных асимптот у рассматриваемой кривой нет, т. к. рассматриваемая функция не имеет конечных пределов, когда x → ±∞.
3.Вычисляя пределы
|
f(x) |
|
|
2x2 + x |
|
|
|
||||
k = lim |
|
|
= |
lim |
|
|
= 2, |
|
|
||
|
|
|
|
||||||||
x→±∞ x |
x→±∞ x(x + 1) |
|
= −1 |
|
|||||||
x→±∞ |
− 2 ] = x→±∞ |
−1 + x + 1 |
|
||||||||
b = lim [f(x) |
|
x |
lim |
1 |
|
|
|
, |
|||
|
|
|
|
|
|
|
|||||
замечаем, что прямая y = 2x−1 является наклонной асимптотой, к которой
точки данной кривой неограниченно приближаются, когда x → +∞ и когда
x → −∞.
Пример 7.4.4.
Требуется провести полное исследование функции график.
f(x) =
x2
x − 1 и построить ее
1.Функция определена при x 6= 1, поэтому ее график будет иметь две ветви, одна из которых располагается в интервале (−∞, 1), а другая в интервале (1, +∞).
2.Найдем точки пересечения графика с осями координат. Если y = 0, òî x = 0,
следовательно, график имеет с осью абсцисс единственную общую точку (0, 0).
Полагая x = 0, получаем y = 0, значит, график пересекает ось ординат в единственной точке (0, 0).

Приложения производной |
132 |
3.Найдем интервалы знакопостоянства. Числитель функции знак не меняет, а знаменатель меняет при x = 1. Поэтому f(x) > 0, когда x (1, +∞), è f(x) 6 0,
когда x (−∞, 1).
4.Свойствами четности и нечетности данная функция не обладает, поскольку ее
область определения не является симметричной относительно точки x = 0. Ñëå-
довательно, ее график не является симметричным ни относительно оси ординат, ни относительно начала координат. Периодической данная функция также не является.
5. Найдем интервалы монотонности функции. Ее производная имеет вид
f 0(x) = |
2x(x − 1) − x2 · 1 |
= |
x(x − 2) |
. |
(x − 1)2 |
|
|||
|
|
(x − 1)2 |
||
Заметим, что при |
x = 1 производная f 0(x) не существует. Если x(x |
− |
2) > 0, |
||||
òî f 0(x) > 0, |
|
|
|
|
|
|
|
à åñëè x(x |
− |
2) < 0, òî |
f 0(x) < 0. Отсюда вытекает, что f(x) |
||||
|
|
|
|
|
|
|
|
возрастает при |
x |
(−∞, 0) (2, +∞) |
è f(x) убывает при x (0, 1) (1, 2). |
||||
Результаты этого анализа представлены на следующей схеме. |
|
|
|||||
6.Исследуем функцию на экстремумы. Ее критическими точками являются x1 = 0 è x2 = 2. В них производная обращается в ноль. В точке x3 = 1 производ-
ная не существует, но в ней рассматриваемая функция не определена, поэтому критической она не является, а значит, исследовать ее на экстремум не нужно. Схема смены знаков производной, которую мы получили на предыдущем шаге, позволяет на основании первого достаточного условия экстремума (см. теорему
7.2.2 на стр. 119) заключить, что x1 = 0 является точкой максимума, а x2 = 2точкой минимума. В точках экстремума fmax = f(0) = 0, fmin = f(2) = 4.
Приложения производной |
|
|
|
|
|
|
|
133 |
7. В окрестности граничных точек области определения имеем |
||||||||
x lim |
( |
x |
) = −∞ |
, |
x + |
f(x) = + |
∞ |
. |
→−∞ |
f |
|
lim |
|
||||
|
|
|
|
→ ∞ |
|
|
||
Отсюда следует, что кривая уходит на |
−∞, |
когда x → −∞, è íà +∞, когда |
||||||
x → +∞. |
|
|
|
|
|
|
|
|
В точке x = 1 функция претерпевает разрыв второго рода, поскольку
x |
1 0 |
f |
( |
x |
) = −∞ |
x |
1+0 |
|
∞ |
. |
|
lim |
|
|
, |
lim f(x) = + |
|
||||
|
→ − |
|
|
|
|
|
→ |
|
|
|
Следовательно, когда |
x приближается к значению |
1 слева, одна ветвь кривой |
||||||||
уходит на −∞, а когда справа другая ветвь уходит на +∞.
8.Найдем асимптоты графика функции.
а) Вертикальной асимптотой является прямая, проходящая через точку x = 1, поскольку
x 1 0 |
−∞ |
, |
x 1+0 |
∞ |
. |
lim f(x) = |
|
lim f(x) = + |
|
||
→ − |
|
|
→ |
|
|
б) Горизонтальных асимптот нет, поскольку функция не стремится к конечному пределу при x → ±∞.
в) Наклонные асимптоты ищем в виде |
y = kx + b, |
ãäå |
|
|
|
|||||||||||
|
|
k = |
lim |
f(x) |
|
= lim |
|
x |
|
= 1, |
|
|
|
|||
|
|
x |
|
|
|
|
||||||||||
|
|
|
x→±∞ |
|
x→±∞ x |
− 1 |
|
|||||||||
x→±∞ |
[ |
( ) − |
|
|
|
|
|
x2 |
|
|
|
x |
|
|||
|
] = x→±∞ x − 1 − |
= x→±∞ x − 1 |
|
|||||||||||||
b = lim |
|
f x |
kx |
|
lim |
|
|
|
|
x |
|
lim |
|
|
= 1. |
|
Следовательно, единственной наклонной асимптотой является прямая y = x + 1,
причем ветви графика неограниченно приближаются к этой прямой при x → −∞
è ïðè x → +∞.
9.Учитывая результаты выполненного нами полного исследования функции, строим ее график. Он изображен на рис. 7.4.4.

Приложения производной |
134 |
x2
Рис. 7.4.4. График функции y = x − 1.
Пример 7.4.5.
Требуется провести полное исследование функции график.
f(x) =
x
1 − x2 и построить ее
1.Функция определена при x 6= ±1, поэтому ее график будет иметь три ветви, причем левая ветвь располагается в интервале (−∞, −1), средняя в интервале
(−1, 1), а правая в интервале (1, +∞).
2. Найдем точки пересечения графика с осями координат. Полагая y = 0, получаем
x = 0, следовательно, график пересекает ось абсцисс в единственной точке (0, 0).
Åñëè x = 0, òî y = 0, значит, график пересекает ось ординат в единственной
точке (0, 0).
3. Найдем интервалы знакопостоянства. Применяя метод интервалов (он изучается в школьном курсе элементарной математики), убеждаемся, что f(x) > 0, когда
x (−∞, −1) (0, 1), è f(x) < 0, когда x (−1, 0) (1, +∞).
4.Данная функция является нечетной, поскольку ее область определения симметрична относительно точки x = 0 и выполняется соотношение
f( x) = |
−x |
= |
− |
x |
= |
− |
f(x). |
|
1 − (−x)2 |
1 − x2 |
|||||||
− |
|
|
|

Приложения производной |
135 |
Следовательно, ее график симметричен относительно начала координат. Периодической данная функция не является.
5. Найдем интервалы монотонности функции. Ее производная имеет вид
f 0(x) = |
|
x |
|
0 |
= |
1 |
|
(1 |
x2) − x · (−2x) |
= |
x2 + 1 |
. |
|
− x2 |
|
|
· |
|
−(1 − x2)2 |
(1 − x2)2 |
|||||
1 |
|
|
|
|
|
|
||||||
Очевидно, что она положительна всюду, где существует, поэтому рассматриваемая функция возрастает всюду, где она определена.
6.Экстремумов нет, поскольку данная функция является монотонной всюду, где она определена.
7.В окрестности граничных точек области определения имеем
lim f(x) = 0, |
lim f(x) = 0. |
x→−∞ |
x→+∞ |
Следовательно, левая ветвь кривой стремится к оси абсцисс, когда x |
→ −∞, |
|||||||||||
а правая, когда x → +∞. |
|
|
|
|
|
|
|
|
|
|
|
|
В точках x = ±1 функция претерпевает разрыв второго рода, так как: |
|
|||||||||||
x→−1−0 |
f |
( |
x |
) = +∞ |
, |
x→−1+0 |
|
|
−∞ |
; |
|
|
lim |
|
|
lim f(x) = |
|
|
|
||||||
x→1−0 |
f |
( |
x |
) = +∞ |
, |
x→1+0 |
|
−∞ |
. |
|
|
|
lim |
|
|
lim f(x) = |
|
|
|
|
|||||
Следовательно, когда x приближается к значению |
−1 слева, левая ветвь кривой |
|||||||||||
уходит на +∞, а когда справа средняя ветвь уходит на |
−∞. В окрестности |
|||||||||||
точки x = 1 ситуация другая: когда |
x приближается к значению |
1 слева, |
||||||||||
средняя ветвь кривой уходит на +∞, |
|
а когда справа правая ветвь уходит на |
||||||||||
−∞. |
|
|
|
|
|
|
|
|
|
|
|
|
8.Найдем асимптоты графика функции.
а) Данная функция имеет две вертикальные асимптоты, проходящие через точ- ки x = ±1. Это следует из анализа поведения функции вблизи точек разрыва, выполненного на предыдущем шаге.
б) Ось абсцисс является единственной горизонтальной асимптотой, к которой неограниченно приближается левая ветвь кривой, когда x → −∞, и правая ее
ветвь, когда x → +∞. Это следует из анализа поведения функции при x → ±∞, выполненного на предыдущем шаге.

Приложения производной |
|
|
|
|
|
|
|
|
|
|
136 |
в) Наклонные асимптоты ищем в виде |
y = kx + b, |
ãäå |
|
||||||||
k = lim |
f(x) |
= lim |
|
|
1 |
|
|
= 0, |
|||
x |
|
|
− x2 |
|
|||||||
x→±∞ |
x→±∞ 1 |
|
|
||||||||
b = x lim [f(x) − kx] = x lim |
|
|
|
x |
|
= 0. |
|||||
|
|
|
|
|
|
||||||
|
1 |
− |
x2 |
||||||||
→±∞ |
|
|
→±∞ |
|
|
|
|
||||
Мы пришли к уже известному нам результату, что прямая y = 0 (ось абсцисс)
является асимптотой. Это и не удивительно: горизонтальную асимптоту, как отмечалось выше, можно рассматривать как наклонную.
9.Учитывая результаты выполненного нами полного исследования функции, строим ее график. Он изображен на рис. 7.4.5.
x
Рис. 7.4.5. График функции y = 1 − x2 .
Пример 7.4.6.
Требуется провести полное исследование функции
f(x) = x3 − 6x2 + 9x − 10
и построить ее график.
1.Функция определена при x.
2.Найдем точки пересечения графика с осями координат. Полагая x = 0, получаем
y = −10, значит, график пересекает ось ординат в единственной точке (0, −10).

Приложения производной |
137 |
Чтобы найти точки пересечения графика с осью абсцисс, нужно решить кубиче- ское уравнение x3 −6x2 + 9x−10 = 0. Это всегда возможно, но соответствующий
математический аппарат достаточно сложен и в программу нашего курса не входит. Как станет ясно из дальнейшего, проведение таких вычислений не является необходимым для схематического построения графика.
3.Найти интервалы знакопостоянства невозможно, если неизвестны точки, в которых график пересекает ось абсцисс.
4.Свойствами четности и нечетности данная функция не обладает. Ее область опре-
деления симметрична относительно точки x = 0, íî ïðè ýòîì f(−x) 6= f(x)
è f(−x) 6= −f(x).
5.Найдем интервалы монотонности функции. Ее производная имеет следующий вид: f 0(x) = 3x2 − 12x + 9 = 3(x − 1)(x − 3). Применяя метод интервалов, убе-
ждаемся, что f 0(x) < 0, когда |
1 < x < 3, è |
f 0(x) > 0, |
когда x < 1 èëè |
x > 3. Отсюда следует, что f(x) |
убывает, когда |
x (1, 3), |
и возрастает, когда |
x (−∞, 1) (3, +∞).
6.Исследуем данную функцию на экстремумы. Ее критическими точками являют-
ñÿ x1 = 1 è x2 = 3. В них производная обращается в ноль: f 0(1) = f 0(3) = 0. Применим второе достаточное условие экстремума (см. теорему 7.2.3 на стр. 119).
Вторая производная исследуемой функции |
f 00(x) = 6x |
− |
12 = 6(x |
− |
2). Подстав- |
|||||
ляя в нее критические точки, заключаем, что f 00(1) = |
|
|
|
|||||||
− |
6 < 0 è |
f 00(3) = 6 > 0. |
||||||||
|
|
|
|
|
|
|
|
|
||
Следовательно, в точке x1 = 1 максимум функции |
f(x), а в точке x2 = 3 |
|||||||||
минимум, причем fmax = f(1) = −6, à fmin = f(3) = −10. |
|
|
||||||||
7. В окрестности граничных точек области определения имеем: |
|
|
||||||||
x |
lim f(x) = |
−∞ |
x |
+ |
|
∞ |
. |
|
|
|
|
|
, |
lim f(x) = + |
|
|
|
|
|||
|
→−∞ |
|
|
→ ∞ |
|
|
|
|
|
|
8.Проверка показывает, что асимптот у данной функции нет.
9.Учитывая результаты выполненного нами исследования функции, строим ее график. Он изображен на рис. 7.4.6.
Замечание.
При построении графика данной функции мы сумели обойтись без информации о точках его пересечения с осью абсцисс. Более того, теперь, когда график построен, мы можем сказать, что он пересекает ось абсцисс ровно один раз и происходит
