8 |
Дифференциал функции |
157 |
|
|
|
Рассмотренные нами понятия приращения и производной функции тесно связаны с понятием ее дифференциала, к изучению которого мы сейчас приступаем.
8.1. Определение дифференциала функции
Ïî определению 6.1.1 (см. стр. 73) производная функции y = f(x) в некоторой фик-
сированной точке x находится по формуле
f 0(x) = lim 4f .
4x→0 4x
Применяя лемму 4.11.1 (см. стр. 53), получаем отсюда
44fx = f 0(x) + α(4x),
ãäå α(4x) бесконечно малая функция при 4x → 0.
Умножая последнее равенство на 4x, получаем формулу для приращения функции
4f = f 0(x)4x + α(4x)4x.
Эта формула показывает, что приращение функции 4f представимо в виде суммы
двух слагаемых. Первое из них и называется дифференциалом функции y = f(x)
в точке x.
Определение 8.1.1.
Дифференциалом df функции y = f(x) в некоторой фиксированной точке
x называется главная (линейная по 4x) часть приращения этой функции 4f, которая находится по формуле
df = f 0(x)4x.
Замечания.
1.Приращение аргумента 4x это просто некоторая переменная величина, имею-
щая числовые значения. В определении дифференциала, в отличие от определения производной, не требуется, чтобы эта величина стремилась к нулю.
Дифференциал функции |
|
|
159 |
|||||
Пример 8.1.2. |
|
|
|
|
|
|
|
|
Пусть |
f(x) = x3 − 3x2 + 3x. Тогда df = (3x2 − 6x + 3)dx = 3(x − 1)2dx. |
|||||||
Пример 8.1.3. |
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
x |
|
Пусть |
2 |
|
Тогда |
|||||
|
|
|
|
|
||||
|
f(x) = |
1 + x |
. |
|
df = √1 + x2 dx. |
|||
Пример 8.1.4. |
|
|
|
|
|
|
|
|
Пусть |
f(x) = ln cos x. Тогда |
df = − tg xdx. |
||||||
8.2. Свойства дифференциала
Основные правила вычисления дифференциала функции фактически ничем не отли- чаются от правил вычисления производной:
1. |
dc = 0, åñëè c = const. |
|||||
2. |
d(u ± v) = du ± dv. |
|||||
3. |
d(uv) = vdu + udv. |
|||||
4. |
d |
u |
|
= |
vdu − udv |
. |
|
|
|||||
|
v |
|
v2 |
|||
Доказательства этих правил тривиальны. Так, например, формула для дифференциала произведения доказывается следующим образом.
d(uv) = (uv) 0dx = (u 0v + uv 0)dx = vu 0dx + uv 0dx = vdu + udv.
8.3. Геометрический смысл дифференциала
Рассматривая геометрический смысл производной функции (см. ðèñ. 6.2.2 на стр. 77), мы доказали, что тангенс угла наклона к оси абсцисс касательной к графику функ-
öèè y = f(x), проведенной в точке с координатами (x, f(x)), совпадает со значением
производной данной функции в этой точке, т. е. tg α = f 0(x).
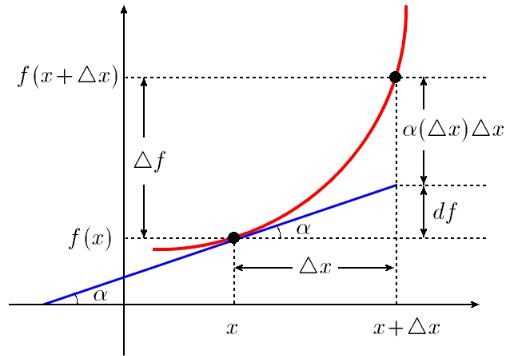
Учитывая, что df = f 0(x)4x, мы можем заключить (см. рис. 8.3.1), что дифференциал
функции в точке x равен приращению функции в этой точке, которое получается, если
Дифференциал функции |
160 |
участок кривой y = f(x) на отрезке |
[x, x + 4x] заменить касательной к этой кривой, |
проведенной в точке с координатами |
(x, f(x)). |
Отметим, что при такой замене мы допускаем погрешность, которая равна α(4x)4x.
Она будет тем меньше по абсолютной величине, чем меньше будет величина 4x. Ïðè
4x → 0 эта погрешность является бесконечно малой величиной, порядок которой выше порядка 4x.
Рис. 8.3.1. Геометрический смысл дифференциала функции.
8.4. Рекомендации
Студентам, испытывающим серьезные трудности при изучении курса высшей математики, рекомендуется в первую очередь разобрать следующие вопросы.
1.Дать определение дифференциала функции.
2.Какова связь между дифференциалом функции и ее производной?